Repérage dans le plan et dans l'espace

Repérage dans le plan et dans l'espace
Les éléments du triplet (x,y,z) sont respectivement appelés abscisse (x), une ordonnée (y) et une cote (z).

En géométrie analytique, tout point du plan ou de l'espace est « repéré », c'est-à-dire qu'on lui associe un couple (dans le plan) ou un triplet (dans l'espace) de nombres.

Sommaire

Préliminaire : droite graduée

Article détaillé : Droite graduée.

Pour graduer une droite, on prend sur cette droite un point O appelé origine et le représentant d'un vecteur \vec{i} passant par O qui définit l'unité: on parle du repère (O, \vec{i}).

Propriété et définition
Sur une droite graduée par le repère (O, \vec {i}), à tout point A correspond un unique nombre x appelé abscisse de A.
On a
\overrightarrow{OA} = x \cdot \vec{i}
et on note A(x).

Repérage dans le plan

Pour munir le plan d'un repère, on prend dans ce plan un point O appelé origine et les représentants de deux vecteurs \vec{i} et \vec{j} passant par O qui définissent les unités respectivement « horizontales » et « verticales » : on parle du repère (O, \vec{i}, \vec{j})\,.

Propriété et définition
Dans le plan muni du repère (O, \vec{i}, \vec{j}),à tout point A correspond un unique couple (x,y) de nombres appelés coordonnées de A. On a
\vec {OA} = x \cdot \vec{i} + y \cdot \vec{j}
et on note A(x,y).
Vocabulaire
x est l' abscisse de A et y est son ordonnée.

La droite sur laquelle on lit les abscisses des points est appelée axe des abscisses et celle sur laquelle on lit les ordonnées des points est appelée axe des ordonnées.

Un repère dont les axes sont perpendiculaires est dit orthogonal . Un repère orthogonal tel que les longueurs (« normes ») de \vec{i} et de \vec{j} soient chacune égales à 1 est dit orthonormé, ou repère orthonormal.

Repérage dans l'espace

Pour munir l'espace d'un repère, on prend un point O appelé origine et les représentants de trois vecteurs \vec{i}, \vec{j} et \vec{k} passant par O qui définissent les unités et les directions, respectivement « gauche-droite », « avant-arrière » et « verticale » : on parle du repère (O, \vec{i}, \vec{j}, \vec{k}).

Propriété et définition
Dans l'espace muni du repère (O, \vec{i}, \vec{j}, \vec{k}), à tout point A correspond un unique triplet (x,y,z) de nombres appelés coordonnées de A. On a
\vec {OA} = x \cdot \vec{i} + y \cdot \vec{j} + z \cdot \vec{k}
et on note A(x,y,z).
Vocabulaire
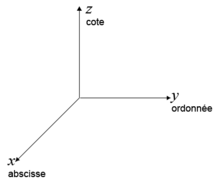
x est l'abscisse de A, y est son ordonnée et z est sa cote.

La droite sur laquelle on lit les abscisses des points est appelée axe des abscisses, celle sur laquelle on lit les ordonnées des points est appelée axe des ordonnées et celle sur laquelle on lit les cotes est appelée axe des cotes.

Un repère dont les axes sont perpendiculaires est dit orthogonal. Un repère orthogonal dont les longueurs de \vec{i}, de \vec{j} et de \vec{k} sont chacune égales à 1 est dit orthonormé, ou repère orthonormal.

Les repères \mathbb{R} et \mathbb{C}

Propriété
À tout point de la droite graduée par le repère (O, \vec{i}) correspond un unique nombre réel.
La réciproque est vraie.
Propriété
À tout point du plan muni du repère (O, \vec{i}, \vec{j}) correspond un unique nombre complexe.
La réciproque est vraie.

Au point (0,1) correspond le nombre complexe i. Ce plan est appelé plan complexe ou 'plan d'Argand-Cauchy

Voir aussi

Articles connexes

v · d · m
Mathématiques élémentaires
Domaines des mathématiques Algèbre classique  · Arithmétique élémentaire  · Analyse  · Analyse réelle  · Suites numériques  · Géométrie classique  · Logique  · Probabilités  · Statistiques
Algèbre classique Addition  · Multiplication  · Division  · Ordre des opérations  · Table d'addition  · Table de multiplication  · Associativité  · Commutativité  · Distributivité  · Transitivité  · Proportionnalité  · Pourcentage  · Règle de trois  · Fraction  · Équation du premier degré  · Équation du second degré  · Système d'équation
Géométrie classique Géométrie du triangle  · Quadrilatère  · Coordonnées cartésiennes  · Théorème de Pythagore  · Théorème de Thalès  · Théorème de Thalès (cercle)  · Théorème des milieux  · Théorème d'Al-Kashi  · Rotation plane  · Homothétie  · Translation  · Similitude
Arithmétique Multiple  · Diviseur  · Division euclidienne  · Nombre premier  · Congruence sur les entiers  · PGCD de nombres entiers  · Plus petit commun multiple  · Critère de divisibilité  · Preuve par neuf
Suites et fonctions Fonction de référence  · Fonction affine  · Fonction du second degré  · Fonction puissance · Fonction trigonométrique  · Fonction logarithme  · Fonction exponentielle  · Suite arithmétique  · Suite géométrique  · Limite  · Dérivation  · Opérations sur les limites  · Dérivées usuelles  · Opérations sur les dérivées
Logique Logique (mathématiques élémentaires)  · Démonstration  · Contre-exemple  · Difficulté mathématique
Statistiques et probabilités Statistiques (mathématiques élémentaires)  · Critères de position  · Critères de dispersion  · Série statistique à deux variables  · Probabilités (mathématiques élémentaires)  · Arbre de probabilité  · Variables aléatoires élémentaires

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Repérage dans le plan et dans l'espace de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Reperage dans le plan et dans l'espace — Repérage dans le plan et dans l espace Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • ESPACE (CONQUÊTE DE L’) - Lanceurs et vaisseaux spatiaux — Les véhicules de lancement sont des vaisseaux autopropulsés, du type «plus lourd que l’air», utilisés pour mettre un vaisseau secondaire ou une charge utile sur une trajectoire balistique. Ils sont proches parents des engins antérieurs, les… …   Encyclopédie Universelle

  • ESPACE-TEMPS — La mécanique classique, sous la forme mathématique rigoureuse que lui a donnée Newton, repose sur les deux concepts fondamentaux d’espace et de temps absolus: un événement ponctuel est parfaitement déterminé lorsqu’on connaît sa position dans… …   Encyclopédie Universelle

  • ESPACE (CONQUÊTE DE L’) - Les premiers programmes spatiaux — La recherche scientifique, l’exploration de l’inconnu et la mise au point de la survie de l’homme dans l’espace furent les buts principaux des premiers programmes spatiaux nationaux. Cependant, de plus en plus, on a mis en service des satellites… …   Encyclopédie Universelle

  • ESPACE (esthétique) — Le problème de l’espace n’aura été longtemps pour l’Occident que celui de la représentation de l’espace. Et la confusion perdure chez plus d’un théoricien. Or, des civilisations qui parfois même ne disposent d’aucun mot pour désigner le milieu à… …   Encyclopédie Universelle

  • Plan réticulaire — Indices de Miller et indices de direction Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction. Un cristal est un… …   Wikipédia en Français

  • Plan cartésien — Coordonnées cartésiennes Un système de coordonnées cartésiennes permet de déterminer la position d un point sur une droite, dans un plan ou dans l espace à condition d avoir défini un repère cartésien. Il permet aussi de caractériser un vecteur.… …   Wikipédia en Français

  • Opérations de l'Axe dans les eaux australiennes — Article principal : Histoire militaire de l Australie pendant la Seconde Guerre mondiale. Affiche de propagande appelant les Australiens à venger le naufrage du navire hôpital Centaur coulé par le sous marin japonais Seconde Guerre mondiale …   Wikipédia en Français

  • PEINTURE - L’espace pictural — Chacun des arts est l’exercice d’une des relations fondamentales entre l’homme et le monde. Ainsi, nés dans une matrice dont nos fantasmes gardent le souvenir, nous trouvons dans l’architecture, espace englobant, une matrice agrandie et… …   Encyclopédie Universelle

  • Première littéraire — La première littéraire dans les études secondaire en France En France, la classe de première littéraire est la deuxième année du lycée, lorsque l’élève a choisi le baccalauréat littéraire. C est une des trois « séries » de la classe de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”