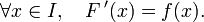- Primitives
-
Primitive
 Pour les articles homonymes, voir Primitive (homonymie).
Pour les articles homonymes, voir Primitive (homonymie).- Cet article fait partie de la série
Primitives de fonctions - Rationnelles
- Logarithmes
- Exponentielles
- Irrationnelles
- Trigonométriques
- Hyperboliques
- Circulaires réciproques
- Hyperboliques réciproques
En mathématiques, une primitive (ou, rarement, antidérivée – de l'anglais antiderivative) d'une fonction f d'une variable réelle définie sur un intervalle I est une fonction F définie et dérivable sur I dont la dérivée est f, autrement dit telle que :
Une condition suffisante pour qu'une fonction f admette des primitives sur un intervalle est qu'elle y soit continue.
Si f est une fonction admettant une primitive F sur un intervalle I, alors pour tout réel k, une primitive de kf sur l'intervalle I est kF.
Si F et G sont des primitives respectives de deux fonctions f et g, alors une primitive de f + g est F + G.
Si une fonction f admet une primitive sur un intervalle, elle en admet une infinité, qui diffèrent d'une constante : si F1 et F2 sont deux primitives de f, alors il existe un réel k0 tel que F1 = F2 + k0.
Si F est une primitive de f, alors
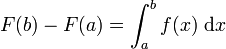 .
.
Ceci est la seconde partie du théorème fondamental de l'analyse.
Sommaire
Exemples
- Une primitive de la fonction
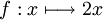 est
est 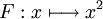
- Une primitive de la fonction
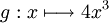 est
est 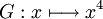
- Une primitive de la fonction
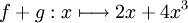 est
est 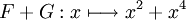
- Une primitive de la fonction
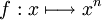 est
est 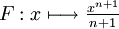 pour n réel différent de −1.
pour n réel différent de −1. - Une primitive de la fonction inverse
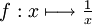 est la fonction logarithme népérien
est la fonction logarithme népérien 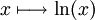 .
. - Dans le cas général, il n'y a pas de manière simple d'avoir la primitive d'une fraction rationnelle sauf en la décomposant en éléments simples.
- Une primitive de la fonction cosinus est la fonction sinus.
- Une primitive de la fonction sinus est l'opposé de la fonction cosinus.
- Autres
- Une primitive de la fonction exponentielle est la fonction exponentielle elle-même.
Calcul automatique
Des logiciels comme Maxima, Maple ou Mathematica permettent depuis quelques années de calculer interactivement certaines primitives sous forme symbolique. Le premier logiciel permettant d'effectuer de l'intégration assistée par ordinateur sous forme symbolique était le langage FORMAC, utilisé par les physiciens dans les années 1970.
Primitives courantes
Article détaillé : table de primitives.Pour le premier tableau, la première colonne est la fonction dont on cherche la primitive, la deuxième est son domaine de dérivation et la troisième, la primitive correspondante à cette fonction.
Pour le second tableau, la première colonne est la fonction dont on cherche la primitive et la seconde, la primitive correspondante à la fonction
Fonctions simples
Soient a,b,C des constantes et k un entier relatif.
Tableau des primitives simples f(x) DD F(x) 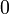

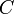
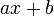

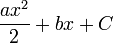
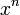 (
(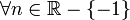 )
) si
si  ;
; 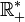 sinon
sinon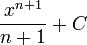
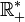
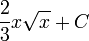

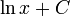
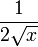
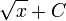
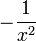
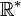
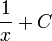
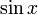

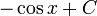
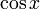

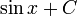
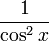
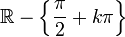
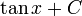
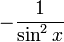
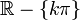
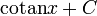
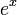

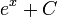
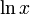
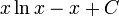
Fonctions composées
Soient u et v deux fonctions.
Tableau des primitives composées f(x) F(x) 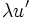
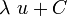
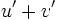
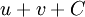
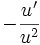
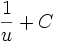
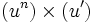
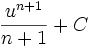
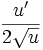
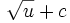
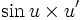
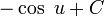
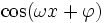
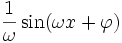
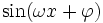
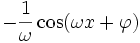
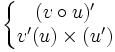
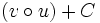
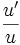
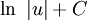

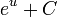
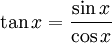
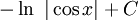
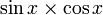
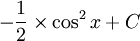
Voir aussi
- Intégrale
- Intégrale impropre
- Table d'intégrales
- Calcul numérique d'une intégrale
- Table de primitives
- Portail des mathématiques
Catégories : Primitive | Analyse réelle - Cet article fait partie de la série
Wikimedia Foundation. 2010.