Primitives de fonctions trigonometriques

Primitives de fonctions trigonometriques

Primitives de fonctions trigonométriques

Cet article fait partie de la série
Primitives de fonctions
Rationnelles
Logarithmes
Exponentielles
Irrationnelles
Trigonométriques
Hyperboliques
Circulaires réciproques
Hyperboliques réciproques
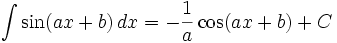
\int \sin(ax+b)\,dx=-\frac{1}{a}\cos(ax+b)+C
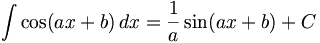
\int \cos(ax+b)\,dx=\frac{1}{a}\sin(ax+b)+C
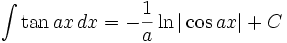
\int \tan ax\,dx=-\frac{1}{a}\ln|\cos ax|+C
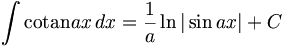
\int \operatorname{cotan} ax\,dx=\frac{1}{a}\ln|\sin ax|+C
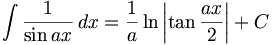
\int \frac{1}{\sin ax}\,dx=\frac{1}{a}\ln\left|\tan \frac{ax}{2}\right|+C
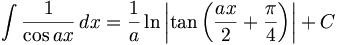
\int \frac{1}{\cos ax}\,dx=\frac{1}{a}\ln\left|\tan \left( \frac{ax}{2}+\frac{\pi}{4}\right)\right|+C
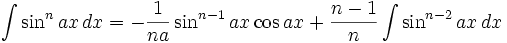\int \sin^n ax\,dx=-\frac{1}{na}\sin^{n-1} ax \cos ax +\frac{n-1}{n}\int \sin^{n-2} ax \,dx (n ∈ ℤ\{0,-1})
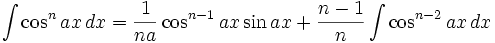\int \cos^n ax\,dx=\frac{1}{na}\cos^{n-1} ax \sin ax +\frac{n-1}{n}\int \cos^{n-2} ax \,dx (n ∈ ℤ\{0,-1})
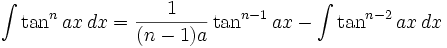\int \tan^n ax\,dx=\frac{1}{(n-1)a}\tan^{n-1} ax -\int \tan^{n-2} ax \,dx (n ∈ ℕ\{0,1})
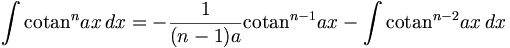\int \operatorname{cotan}^n ax\,dx=-\frac{1}{(n-1)a}\operatorname{cotan}^{n-1} ax -\int \operatorname{cotan}^{n-2} ax \,dx (n ∈ ℕ\{0,1})
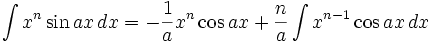\int x^n\sin ax\,dx=-\frac{1}{a}x^n\cos ax +\frac{n}{a}\int x^{n-1}\cos ax \,dx (n ∈ ℤ\{-1})
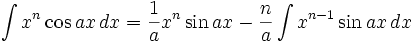\int x^n\cos ax\,dx=\frac{1}{a}x^n\sin ax -\frac{n}{a}\int x^{n-1}\sin ax \,dx (n ∈ ℤ\{-1})
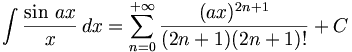
\int \frac{\sin\,ax}{x}\,dx=\sum_{n=0}^{+\infty}\frac{(ax)^{2n+1}}{(2n+1)(2n+1) !}+C
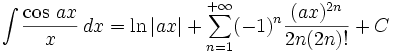
\int \frac{\cos\,ax}{x}\,dx=\ln|ax|+\sum_{n=1}^{+\infty}(-1)^n\frac{(ax)^{2n}}{2n(2n)!}+C
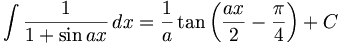
\int \frac{1}{1+\sin ax}\,dx=\frac{1}{a}\tan\left(\frac{ax}{2}-\frac{\pi}{4}\right)+C
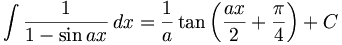
\int \frac{1}{1-\sin ax}\,dx=\frac{1}{a}\tan\left(\frac{ax}{2}+\frac{\pi}{4}\right)+C
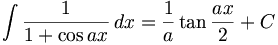
\int \frac{1}{1+\cos ax}\,dx=\frac{1}{a}\tan\frac{ax}{2}+C
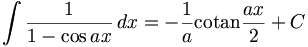
\int \frac{1}{1-\cos ax}\,dx=-\frac{1}{a}\operatorname{cotan}\frac{ax}{2}+C
Ce document provient de « Primitives de fonctions trigonom%C3%A9triques ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Primitives de fonctions trigonometriques de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”