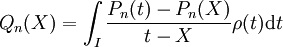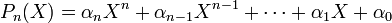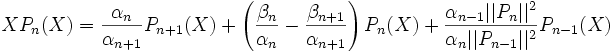Polynômes secondaires
- Polynômes secondaires
-
Polynôme secondaire
Introduction et définition
On se place sur l'espace de Hilbert 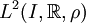 où I est un intervalle de
où I est un intervalle de  et ρ la densité de la mesure.
et ρ la densité de la mesure.
Les polynômes secondaires associés aux polynômes orthogonaux 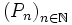 sont les polynômes
sont les polynômes 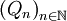 obtenus par la relation :
obtenus par la relation :
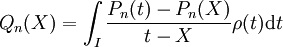
Ces polynômes ne sont plus orthogonaux, mais suivent la même relation de récurrence que les Pn :
si Pn s'écrit : 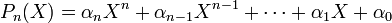
alors la relation de récurrence est :
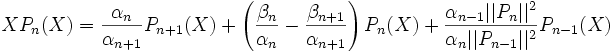
Polynômes secondaires des polynômes orthogonaux classiques
Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !
Voir aussi
Les polynômes secondaires sont à la base de la théorie des mesures secondaires.
 Portail des mathématiques
Portail des mathématiques
Catégories : Algèbre | Analyse
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Polynômes secondaires de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Polynomes orthogonaux — Polynômes orthogonaux Sommaire 1 Introduction 1.1 Exemple : les polynômes de Legendre 2 Propriétés des suites de polynômes orthogonaux 2.1 Re … Wikipédia en Français
Polynômes orthogonaux — En mathématiques, une suite de polynômes orthogonaux est une suite infinie de polynômes p0(x), p1(x), p2(x) ... à coefficients réels, dans laquelle chaque pn(x) est de degré n, et telle que les polynômes de la suite sont orthogonaux deux à deux… … Wikipédia en Français
Polynômes de Legendre — Polynôme de Legendre Polynômes de Legendre Les polynômes de Legendre sont des solutions y de l équation différentielle de Legendre. Sommaire 1 … Wikipédia en Français
Mesures Secondaires — Mesure secondaire En mathématiques, la mesure secondaire associée à une mesure de densité positive ρ est, lorsqu elle existe, une mesure de densité positive μ qui rend orthogonaux les polynômes secondaires associés aux polynômes orthogonaux pour… … Wikipédia en Français
Mesures secondaires — Mesure secondaire En mathématiques, la mesure secondaire associée à une mesure de densité positive ρ est, lorsqu elle existe, une mesure de densité positive μ qui rend orthogonaux les polynômes secondaires associés aux polynômes orthogonaux pour… … Wikipédia en Français
Mesure secondaire — En mathématiques, la mesure secondaire associée à une mesure de densité positive ρ est, lorsqu elle existe, une mesure de densité positive μ qui rend orthogonaux les polynômes secondaires associés aux polynômes orthogonaux pour ρ. Sommaire 1… … Wikipédia en Français
Transformee de Stieltjes — Transformée de Stieltjes En mathématiques, la transformée de Stieltjes d une mesure de densité ρ sur un intervalle I est une fonction de la variable complexe z, définie à l extérieur de cet intervalle par la formule : . Sous certaines… … Wikipédia en Français
Transformée de Stieltjes — En mathématiques, la transformée de Stieltjes d une mesure de densité ρ sur un intervalle I est une fonction de la variable complexe z, définie à l extérieur de cet intervalle par la formule : . Sous certaines conditions on peut reconstituer … Wikipédia en Français
Transformée de stieltjes — En mathématiques, la transformée de Stieltjes d une mesure de densité ρ sur un intervalle I est une fonction de la variable complexe z, définie à l extérieur de cet intervalle par la formule : . Sous certaines conditions on peut reconstituer … Wikipédia en Français
Polynome secondaire — Polynôme secondaire Introduction et définition On se place sur l espace de Hilbert où I est un intervalle de et ρ la densité de la mesure. Les polynômes secondaires associés aux polynômes orthogonaux sont les polynômes … Wikipédia en Français
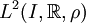 où I est un intervalle de
où I est un intervalle de  et ρ la densité de la mesure.
et ρ la densité de la mesure.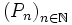 sont les polynômes
sont les polynômes 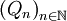 obtenus par la relation :
obtenus par la relation :