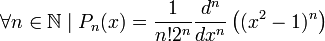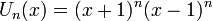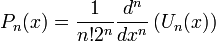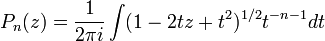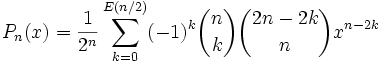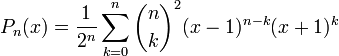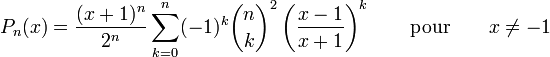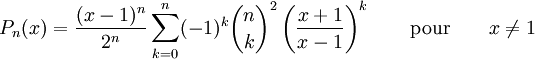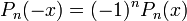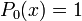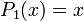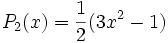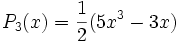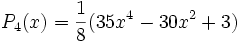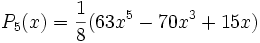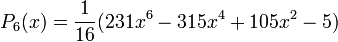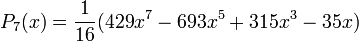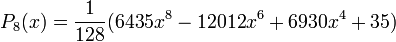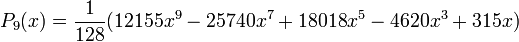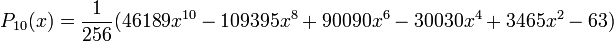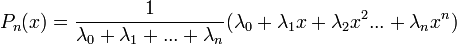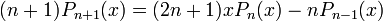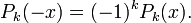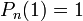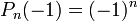Polynômes de Legendre

Polynôme de Legendre

Polynômes de Legendre

Les polynômes de Legendre sont des solutions y de l'équation différentielle de Legendre.

Sommaire

1 Équation de Legendre
2 Autres définitions
- 2.1 Définition classique
- 2.2 Définitions analytiques
3 Matrice de la fonction polynôme de Legendre
4 Valeurs propres
5 Quelques polynômes
6 Orthogonalité
- 6.1 Orthonormalité
7 Autres propriétés
- 7.1 Parité
- 7.2 Points particuliers
8 Applications en physique
9 Voir aussi
10 Notes
11 Bibliographie
12 Références

Équation de Legendre

On appelle équation de Legendre l'équation : $\frac{d}{dx}[(1-x^{2})\frac{dy}{dx}]+n(n+1)y=0$

où n est un entier naturel représentant l'ordre du polynôme.

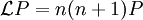
On définit ainsi le polynôme de Legendre $\mathcal{L}P=n(n+1)P$

Autres définitions

Définition classique

On définit simplement le polynôme comme:

$\forall n\in\mathbb N \mid P_n(x)=\frac{1}{n! 2^n}\frac{d^n}{dx^n}\left((x^2-1)^n\right)$

On définit également, pour n entier naturel:

$\ U_n(x)=(x+1)^n(x-1)^n$

$\ P_n(x)=\frac{1}{n! 2^n}\frac{d^n}{dx^n}\left(U_n(x)\right)$

Définitions analytiques

On peut aussi les définir par l'intégrale de contour :

$P_{n}(z)=\frac{1}{2\pi i}\int(1-2tz+t^{2})^{1/2}t^{-n-1}dt$

où le contour entoure l'origine et est pris dans le sens des aiguilles d'une montre.

On définit ce polynôme sous forme de plusieurs sommes:

$P_{n}(x)=\frac{1}{2^n}\sum_{k=0}^{E(n/2)} (-1)^k \binom{n}{k} \binom{2n-2k}{n}x^{n-2k}$

$P_{n}(x)=\frac{1}{2^n}\sum_{k=0}^{n} \binom{n}{k}^2 (x-1)^{n-k}(x+1)^{k}$

$P_{n}(x)=\frac{(x+1)^n}{2^n}\sum_{k=0}^{n} (-1)^k \binom{n}{k}^2 \left(\frac{x-1}{x+1}\right)^k \qquad \mathrm{pour}\qquad x \ne -1$

ou encore par:

$P_{n}(x)=\frac{(x-1)^n}{2^n}\sum_{k=0}^{n} (-1)^k \binom{n}{k}^2 \left(\frac{x+1}{x-1}\right)^k \qquad \mathrm{pour}\qquad x \ne 1$

Ces formulations permettent de calculer certaines valeurs intéressantes des polynômes.On obtient ainsi que la parité du polynôme dépend de la parité de n:

$P_n(-x)=(-1)^nP_n(x)\,$

Matrice de la fonction polynôme de Legendre

$\begin{pmatrix} 0 & 0 & -2 & 0 & 0 & \vdots & 0 &\vdots & 0\\ 0 & 2 & 0 & -6 & 0 &\vdots & 0&\vdots & \vdots\\ 0 & 0 & 6 & 0 & -12 &\vdots & 0 &\vdots & \vdots\\ 0 & 0 & 0 & 12 & 0 &\vdots & 0 &\vdots & \vdots\\ 0 & 0 & 0 & 0 & 20 &\vdots & 0 &\vdots & \vdots \\ \dots & \dots & \dots & \dots & \dots &\ddots & \vdots &\dots & \vdots \\ 0 & 0 & 0 & 0 & 0 &\dots & k(k+1) &\dots & \vdots \\ \dots & \dots & \dots & \dots & \dots &\dots & \dots &\ddots & \vdots \\ 0 & 0 & 0 & 0 & 0 &\dots & 0 &\dots & n(n+1)\\ \end{pmatrix}$

On remarquera que les vecteurs propres de cette matrice sont colinéaires aux polynômes.^[1]

Valeurs propres

La matrice est triangulaire supérieure. Les valeurs propres sont k(k+1), pour k variant de 0 à n.

Quelques polynômes

Les premiers polynômes sont :

Les 20 premiers polynômes de Legendre.

$P_{0}(x)=1 \,$
$P_{1}(x)=x\,$
$P_{2}(x)=\frac{1}{2}(3x^{2}-1)\,$
$P_{3}(x)=\frac{1}{2}(5x^{3}-3x)\,$
$P_{4}(x)=\frac{1}{8}(35x^{4}-30x^{2}+3)\,$
$P_{5}(x)=\frac{1}{8}(63x^{5}-70x^{3}+15x)\,$
$P_{6}(x)=\frac{1}{16}(231x^{6}-315x^{4}+105x^{2}-5)\,$
$P_{7}(x)=\frac{1}{16}(429x^{7}-693x^{5}+315x^{3}-35x)\,$
$P_{8}(x)=\frac{1}{128}(6435x^{8}-12012x^{6}+6930x^{4}+35)\,$
$P_{9}(x)=\frac{1}{128}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)\,$
$P_{10}(x)=\frac{1}{256}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63)\,$

On remarquera que pour n supérieur à 2:

$P_{n}(x)=\frac{1}{\lambda_0+\lambda_1+...+\lambda_n}(\lambda_0+\lambda_1x+\lambda_2x^2...+\lambda_nx^n) \,$

La relation de récurrence entre les différents polynômes s'écrit:

$(n+1)P_{n+1}(x)=(2n+1)xP_{n}(x) - nP_{n-1}(x)\,$

Orthogonalité

Les polynômes orthogonaux les plus simples sont les polynômes de Legendre pour lesquels l'intervalle d'orthogonalité est [−1, 1] et la fonction poids est simplement la fonction constante de valeur 1: Ces polynômes sont orthogonaux par rapport au produit scalaire $\varphi$ défini sur $\R[X]$ par la relation :

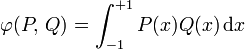$\varphi(P,\, Q) = \int_{-1}^{+1} P(x) Q(x)\, \mathrm{d}x$ .

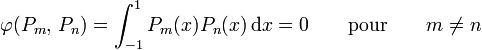
$\varphi(P_m,\, P_n) = \int_{-1}^{1} P_m(x)P_n(x)\,\mathrm{d}x = 0\qquad \mathrm{pour}\qquad m \ne n$

Orthonormalité

La norme, calculée comme $\sqrt[]{\int_{0}^{1} P_n^2(x)\,\mathrm{d}x}$ , est:

$||P_n||=\sqrt[]{\frac{1}{2n+1}}$

On peut remarquer que $P n$ est orthogonal à $R n - 1$ [X] donc $< P n, P' n - 1 > = 0$ De plus on peut établir la relation $P' n + 1 - P' n - 1 = (4 n + 2) P n$ ceci pour n>1. Et on démontre que $< P n, P' m > = 2$ si m-n est impair et positif. Alors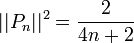 $||P_n||^2={\frac{2}{4n+2}}$

Au final, on a $||P_n||=\sqrt[]{\frac{1}{2n+1}}$

Autres propriétés

Parité

Les polynômes de Legendre suivent la parité de n .On peut exprimer cette proprieté comme:

$P_k(-x) = (-1)^k P_k(x). \,$

On démontre cette proprieté a l'aide des définitions sous forme de somme.

Points particuliers

Comme beaucoup de polynômes orthogonaux classiques comme les polynômes de Tchebychev et d'Hermite les polynômes sont rigoureusement définis. Les propriétés suivantes sont démontrées facilement en étudiant la parité des polynômes et les conditions aux bornes.

$P_{n}(1) = 1 \,$

$P_{n}(-1) = (-1)^n \,$

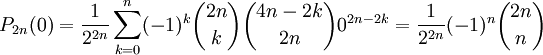$P_{2n}(0)=\frac{1}{2^{2n}}\sum_{k=0}^{n} (-1)^k \binom{2n}{k} \binom{4n-2k}{2n}0^{2n-2k}=\frac{1}{2^{2n}}(-1)^n\binom{2n}{n} \,$ car la somme se réduit au terme d'indice

k = n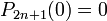

$P_{2n+1}(0) = 0 \,$

Applications en physique

Voir aussi

Notes

↑ Banque PT ,TSI Algebre,Géométrie,Analyse,Editions Ellipse 1993 ,

Bibliographie

I.S. Gradshteyn & I.M. Ryzhik ; Table of Integrals, Series, and Products, Alan Jeffrey and Daniel Zwillinger (eds.), Academic Press (6^e édition - 2000), ISBN 0-12-294757-6. Errata sur le site web des éditeurs : www.mathtable.com

De Nockere ;Tables numériques des polynômes de Legendre , ARB (8e edition - 1949 ) Académie Royale des Sciences des Lettres des Beaux Arts de Belgique

Références

Sujet de l'Ecole Polytechnique 2005 PC: http://www.imprimerie.polytechnique.fr/EnLignes/Files/05_MathPC.pdf

Portail des mathématiques

Ce document provient de « Polyn%C3%B4me de Legendre ».

Catégories : Espace de Hilbert | Fonction hypergéométrique | Méthode mathématique de la physique | Polynôme remarquable | Fonctions spéciales

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Polynômes de Legendre de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Polynomes orthogonaux — Polynômes orthogonaux Sommaire 1 Introduction 1.1 Exemple : les polynômes de Legendre 2 Propriétés des suites de polynômes orthogonaux 2.1 Re … Wikipédia en Français
LEGENDRE (A. M.) — LEGENDRE ADRIEN MARIE (1752 1833) Mathématicien français né et mort à Paris. L’ouvrage qui rendit célèbre Adrien Marie Legendre a pour titre Éléments de géométrie (1794). Il représente un des premiers essais de formalisation rigoureuse de la… … Encyclopédie Universelle
Polynômes orthogonaux — En mathématiques, une suite de polynômes orthogonaux est une suite infinie de polynômes p0(x), p1(x), p2(x) ... à coefficients réels, dans laquelle chaque pn(x) est de degré n, et telle que les polynômes de la suite sont orthogonaux deux à deux… … Wikipédia en Français
Polynôme de Legendre — Polynômes de Legendre Les polynômes de Legendre sont des solutions de l équation différentielle de Legendre, et constituent l exemple le plus simple d une suite de polynômes orthogonaux. Sommaire … Wikipédia en Français
Polynome de Legendre — Polynôme de Legendre Polynômes de Legendre Les polynômes de Legendre sont des solutions y de l équation différentielle de Legendre. Sommaire 1 … Wikipédia en Français
Polynôme de legendre — Polynômes de Legendre Les polynômes de Legendre sont des solutions y de l équation différentielle de Legendre. Sommaire 1 … Wikipédia en Français
Adrien-Marie Legendre — Pour les articles homonymes, voir Legendre. Adrien Marie Legendre Portrait charge de Adrien Marie Legendre[1] … Wikipédia en Français
ORTHOGONAUX (POLYNÔMES) — C’est à travers l’étude de certains problèmes d’analyse fonctionnelle (équations intégrales, séries de Fourier, problème de Sturm Liouville et, plus généralement, problèmes aux limites dans les équations aux dérivées partielles) qu’est apparue la … Encyclopédie Universelle
Filtre De Legendre — Le filtre de Legendre, également appelé filtre de Papoulis, du nom de son inventeur (1958), ou encore filtre optimal a été conçu pour présenter à la fois une atténuation strictement monotone (pas d ondulation, à l inverse des filtres de… … Wikipédia en Français
Filtre de legendre — Le filtre de Legendre, également appelé filtre de Papoulis, du nom de son inventeur (1958), ou encore filtre optimal a été conçu pour présenter à la fois une atténuation strictement monotone (pas d ondulation, à l inverse des filtres de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Polynômes de Legendre

Polynôme de Legendre

Sommaire

Équation de Legendre