Polynômes de Zernike

Polynômes de Zernike
Tracés des polynômes de Zernike sur le disque unité.

Les polynômes de Zernike sont une série de polynômes qui sont orthogonaux sur le disque unité. Ils portent le nom de Frits Zernike ; ils jouent un rôle important en optique géométrique.

Sommaire

Définition des polynômes

Les polynômes de Zernike peuvent se décomposer en fonctions paire et impaire. Les fonctions paires sont :

Z^{m}_n(\rho,\varphi) = R^m_n(\rho)\,\cos(m\,\varphi) \!

et les fonctions impaires sont :

Z^{-m}_n(\rho,\varphi) = R^m_n(\rho)\,\sin(m\,\varphi), \!

où m et n sont des nombres entiers naturels non nuls, avec n≥m, φ est l'angle d'azimuth exprimé en radians, et ρ est la distance radiale normalisée. Les polynômes radiaux Rmn sont définis tels que :

R^m_n(\rho) = \! \sum_{k=0}^{(n-m)/2} \!\!\! \frac{(-1)^k\,(n-k)!}{k!\,((n+m)/2-k)!\,((n-m)/2-k)!} \;\rho^{n-2\,k}

ou

R^m_n(\rho) = \frac{\Gamma(n+1){}_2F_{1}(-\frac{1}{2}(|m|+n),\frac{1}{2}(|m|-n);-n;\rho^{-2})}{\Gamma(\frac{1}{2}(2+n+m))\Gamma(\frac{1}{2}(2+n-m))}\rho^n

pour n − m pair, et sont égaux à 0 pour n − m impair.

Pour m = 0, le polynôme se réduit à Rn0(ρ).

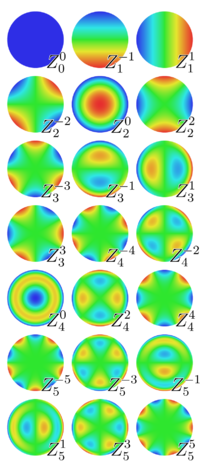
Exemples

Les premiers polynômes de Zernike sont :

R^0_0(r) = 1 \,
R^1_1(r) = r \,
R^0_2(r) = 2r^2 - 1 \,
R^2_2(r) = r^2 \,
R^1_3(r) = 3r^3 - 2r \,
R^3_3(r) = r^3 \,
R^0_4(r) = 6r^4 - 6r^2 + 1 \,
R^2_4(r) = 4r^4 - 3r^2 \,
R^4_4(r) = r^4 \,
R^1_5(r) = 10r^5 - 12r^3 + 3r \,
R^3_5(r) = 5r^5 - 4r^3 \,
R^5_5(r) = r^5 \,
R^0_6(r) = 20r^6 - 30r^4 + 12r^2 - 1 \,
R^2_6(r) = 15r^6 - 20r^4 + 6r^2 \,
R^4_6(r) = 6r^6 - 5r^4 \,
R^6_6(r) = r^6. \,

Annexes

Articles connexes

Liens externes

Bibliographie


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Polynômes de Zernike de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Frederik Zernike — Frederik « Frits » Zernike (16 juillet 1888 à Amsterdam – 10 mars 1966) était un physicien néerlandais. Il est lauréat du prix Nobel de physique de 1953 « pour la démonstration de la méthode de contraste de phase, particulièrement… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”