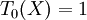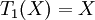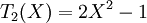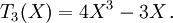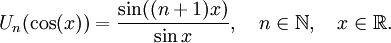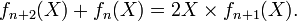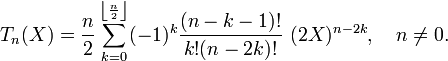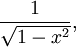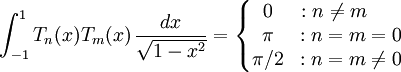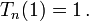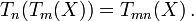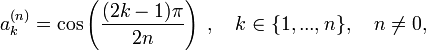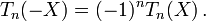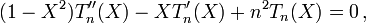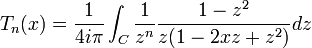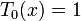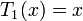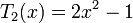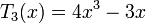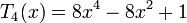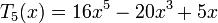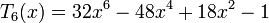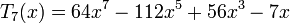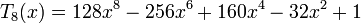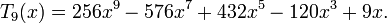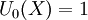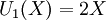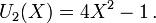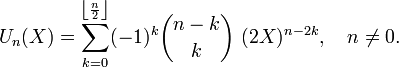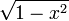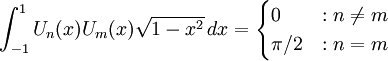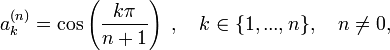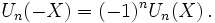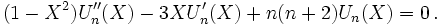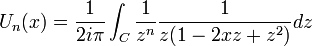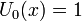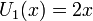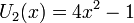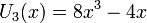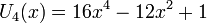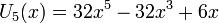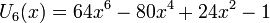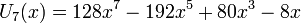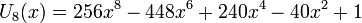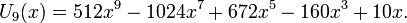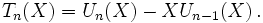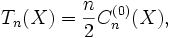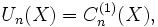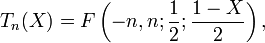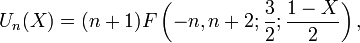Polynômes de Chebyshev

Polynôme de Tchebychev

Les polynômes de Tchebychev sont nommés d'après le mathématicien Pafnouti Tchebychev. Ils forment une famille de polynômes indexés par les entiers. Le polynôme de Tchebychev (de première espèce) $T n$ d'indice $n = 0,1,2,...$ est uniquement défini par la propriété suivante : pour tout nombre réel $x$ ,

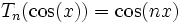$T_{n}(\cos(x)) = \cos(nx) \,$ .

Les premiers polynômes de Tchebychev sont :

$T_0(X)=1\,$

$T_1(X)=X\,$

$T_2(X)=2X^2-1\,$

$T_3(X)=4X^3-3X\,.$

Il existe aussi des polynômes de Tchebychev de seconde espèce, $U n$ définis par :

$U_{n}(\cos(x)) = \frac{\sin((n+1) x)}{\sin x},\quad n\in \N,\quad x\in\R.\,$

Les polynômes de Tchebychev sont uniques, ils forment une famille de polynômes orthogonaux par rapport à une fonction poids définie plus bas.
Les polynômes de Tchebychev $T n$ , $U n$ sont de degré $n$ , ils vérifient tous les deux la relation de récurrence suivante :

$f_{n+2}(X)+f_{n}(X) = 2X \times f_{n+1}(X).$

Sommaire

1 Propriétés des polynômes de Tchebychev de 1^re espèce
2 Propriétés des polynômes de Tchebychev de 2^e espèce
3 Quelques relations avec d'autres fonctions spéciales
4 Intérêt
5 Bibliographie

Propriétés des polynômes de Tchebychev de 1^re espèce

On a :

$T_n(X)=\frac{n}{2}\sum_{k=0}^{\left\lfloor \frac{n}{2} \right \rfloor}(-1)^k \frac{(n-k-1)!}{k!(n-2k)!}~(2X)^{n-2k},\quad n\ne0.$

T_n forme une suite de polynômes orthogonaux avec le poids

$\frac{1}{\sqrt{1-x^2}},$

sur l'intervalle ]−1,1[, c'est-à-dire :

$\int_{-1}^1 T_n(x)T_m(x)\,\frac{dx}{\sqrt{1-x^2}}=\left\{ \begin{matrix} 0 &: n\ne m~~\\ \pi &: n=m=0\\ \pi/2 &: n=m\ne 0 \end{matrix} \right.$

Quel que soit $n$

$T_{n}(1)=1\,.$

Quels que soient $m$ et $n$

$T_{n}(T_{m}(X))=T_{mn}(X)\,.$

Les valeurs :

$a_k^{(n)} = \cos\left(\frac{(2k-1)\pi}{2n}\right)\;,\quad k\in\{1,...,n\},\quad n\ne0,$

sont les $n$ racines de $T n$ .

La parité dépend de $n$ :

$T_{n}(-X)=(-1)^nT_{n}(X)\,.$

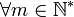$\forall m \in \mathbb N^*$ Le coefficient dominant est : $2 m - 1$

Ils vérifient l'équation différentielle suivante :

$(1-X^2)T_{n}''(X)-XT_n'(X)+n^2T_n(X)=0\,,$

Représentation intégrale :

$T_n(x)=\frac{1}{4i\pi}\int_C\frac{1}{z^n}\frac{1-z^2}{z(1-2xz+z^2)}dz\,$

avec $C$ un contour dans plan complexe autour de zéro, dans le sens positif. Les zéros de $(z - 2 x z + z 2)$ étant en dehors de $C$ .

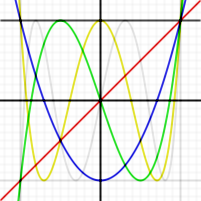Les premiers polynômes de Tchebychev de première espèce sur le domaine −1¼ < x < 1¼, −1¼ < y < 1¼; la fonction constante T₀, et T₁, T₂, T₃, T₄ et T₅.

Les premiers polynômes de Tchebychev de première espèce sont :

$T_0(x) = 1 \,$

$T_1(x) = x \,$

$T_2(x) = 2x^2 - 1 \,$

$T_3(x) = 4x^3 - 3x \,$

$T_4(x) = 8x^4 - 8x^2 + 1 \,$

$T_5(x) = 16x^5 - 20x^3 + 5x \,$

$T_6(x) = 32x^6 - 48x^4 + 18x^2 - 1 \,$

$T_7(x) = 64x^7 - 112x^5 + 56x^3 - 7x \,$

$T_8(x) = 128x^8 - 256x^6 + 160x^4 - 32x^2 + 1 \,$

$T_9(x) = 256x^9 - 576x^7 + 432x^5 - 120x^3 + 9x. \,$

Propriétés des polynômes de Tchebychev de 2^e espèce

les premiers polynômes sont :

$U_0(X)=1\,$

$U_1(X)=2X\,$

$U_2(X)=4X^2-1\,.$

Pour tout réel $X$ , on a :

$U_n(X)=\sum_{k=0}^{\left\lfloor \frac{n}{2} \right \rfloor}(-1)^k \binom{n-k}{k}~(2X)^{n-2k},\quad n\ne0.$

les polynômes de Tchebychev de seconde espèce sont orthogonaux avec le poids

$\sqrt{1-x^2}$

sur l'intervalle [−1,1], c'est-à-dire :

$\int_{-1}^1 U_n(x)U_m(x)\sqrt{1-x^2}\,dx = \begin{cases} 0 &: n\ne m\\ \pi/2 &: n=m \end{cases}$

Pour tout $n$ entier

U n (1) = n + 1,

Les valeurs

$a_k^{(n)} = \cos\left(\frac{k\pi}{n+1}\right)\;,\quad k\in\{1,...,n\},\quad n\ne0,$

sont les $n$ racines de $U n$ .

La parité dépend de $n$ :

$U_{n}(-X)=(-1)^nU_{n}(X)\,.$

Ils vérifient l'équation différentielle suivante:

$(1-X^2)U_{n}''(X)-3XU_n'(X)+n(n+2)U_n(X)=0\,.$

Représentation intégrale :

$U_n(x)=\frac{1}{2i\pi}\int_C\frac{1}{z^n}\frac{1}{z(1-2xz+z^2)}dz\,$

avec $C$ un contour dans plan complexe autour de zéro, dans le sens positif. Les zéros de $(z - 2 x z + z 2)$ étant en dehors de $C$ .

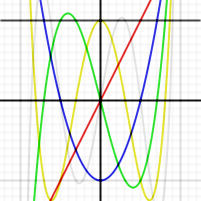Les premiers polynômes de Tchebychev de seconde espèce sur le domaine −1¼ < x < 1¼, −1¼ < y < 1¼; la fonction constante U₀, et U₁, U₂, U₃, U₄ et U₅.

Les premiers polynômes de Tchebychev de seconde espèce sont :

$U_0(x) = 1 \,$

$U_1(x) = 2x \,$

$U_2(x) = 4x^2 - 1 \,$

$U_3(x) = 8x^3 - 4x \,$

$U_4(x) = 16x^4 - 12x^2 + 1 \,$

$U_5(x) = 32x^5 - 32x^3 + 6x \,$

$U_6(x) = 64x^6 - 80x^4 + 24x^2 - 1 \,$

$U_7(x) = 128x^7 - 192x^5 + 80x^3 - 8x \,$

$U_8(x) = 256x^8 - 448 x^6 + 240 x^4 - 40 x^2 + 1 \,$

$U_9(x) = 512x^9 - 1024 x^7 + 672 x^5 - 160 x^3 + 10 x. \,$

Quelques relations avec d'autres fonctions spéciales

$T_{n}(X)=U_{n}(X)-X U_{n-1}(X)\,.$

$T_{n}(X)=\frac{n}{2}C_{n}^{(0)}(X),$

$U_{n}(X)=C_{n}^{(1)}(X),$

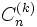avec $C_n^{(k)}$ un polynôme de Gegenbauer et

$T_{n}(X)=F\left(-n,n;\frac{1}{2};\frac{1-X}{2}\right),$

$U_{n}(X)=(n+1)F\left(-n,n+2;\frac{3}{2};\frac{1-X}{2}\right),$

avec $F$ la fonction hypergéométrique.

Intérêt

Tchebychev a découvert ceux-ci en travaillant sur le problème de convergence des interpolations de Lagrange. On peut démontrer que pour minimiser l'erreur engendrée par l'interpolation (cf. phénomène de Runge), il faut choisir les racines des polynômes de Tchebychev comme points d'interpolation. Dans ce contexte, ces 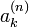$a_k^{(n)}$ données ci-dessus, éventuellement ajustés à un autre intervalle d'interpolation [a,b] considéré (par une transformation affine 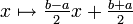$x\mapsto\tfrac{b-a}{2}x+\tfrac{b+a}{2}$ ), sont appelés les abscisses de Tchebychev.

Les polynômes de Tchebychev sont impliqués dans le calcul de filtres en électronique analogique, les filtres de Tchebychev.

Ils peuvent également servir à démontrer le théorème de Weierstrass (Toute fonction continue sur un intervalle I est limite uniforme d'une suite de polynômes).

Bibliographie

Polynômes de Tchebychev sur Math-Linux.
(en) Abramowitz and Stegun, Handbook of Mathematical Functions, chap. 22.

Portail des mathématiques

Ce document provient de « Polyn%C3%B4me de Tchebychev ».

Catégories : Fonction hypergéométrique | Polynôme remarquable | Fonctions spéciales | Interpolation polynomiale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Polynômes de Chebyshev de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Chebyshev — Pafnouti Tchebychev Pafnouti Tchebychev Pafnouti Lvovitch Tchebychev (en russe : Пафнутий Львович Чебышёв) (4 mai 1821 à Okatovo, près de Boro … Wikipédia en Français
Pafnuty Chebyshev — Pafnouti Tchebychev Pafnouti Tchebychev Pafnouti Lvovitch Tchebychev (en russe : Пафнутий Львович Чебышёв) (4 mai 1821 à Okatovo, près de Boro … Wikipédia en Français
Théorie de l'approximation — En mathématiques, la théorie de l approximation concerne la façon dont les fonctions peuvent être approchées par de plus simples fonctions, en donnant une caractérisation quantitative des erreurs introduites par ces approximations. Un problème… … Wikipédia en Français
Theorie de l'approximation — Théorie de l approximation En mathématiques, la théorie de l approximation concerne la façon dont les fonctions peuvent être approchées par de plus simples fonctions, en donnant une caractérisation quantitative des erreurs introduites par ces… … Wikipédia en Français
Chebychev — Pafnouti Tchebychev Pafnouti Tchebychev Pafnouti Lvovitch Tchebychev (en russe : Пафнутий Львович Чебышёв) (4 mai 1821 à Okatovo, près de Boro … Wikipédia en Français
Pafnouti Lvovitch Tchebychev — Pafnouti Tchebychev Pafnouti Tchebychev Pafnouti Lvovitch Tchebychev (en russe : Пафнутий Львович Чебышёв) (4 mai 1821 à Okatovo, près de Boro … Wikipédia en Français
Pafnouti Tchebyshev — Pafnouti Tchebychev Pafnouti Tchebychev Pafnouti Lvovitch Tchebychev (en russe : Пафнутий Львович Чебышёв) (4 mai 1821 à Okatovo, près de Boro … Wikipédia en Français
Pafnouti Tchebytchev — Pafnouti Tchebychev Pafnouti Tchebychev Pafnouti Lvovitch Tchebychev (en russe : Пафнутий Львович Чебышёв) (4 mai 1821 à Okatovo, près de Boro … Wikipédia en Français
Pafnouti Tchébycheff — Pafnouti Tchebychev Pafnouti Tchebychev Pafnouti Lvovitch Tchebychev (en russe : Пафнутий Львович Чебышёв) (4 mai 1821 à Okatovo, près de Boro … Wikipédia en Français
Tchebychev — Pafnouti Tchebychev Pafnouti Tchebychev Pafnouti Lvovitch Tchebychev (en russe : Пафнутий Львович Чебышёв) (4 mai 1821 à Okatovo, près de Boro … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Polynômes de Chebyshev

Polynôme de Tchebychev

Sommaire

Propriétés des polynômes de Tchebychev de 1^re espèce

Propriétés des polynômes de Tchebychev de 2^e espèce

Quelques relations avec d'autres fonctions spéciales

Intérêt

Bibliographie

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Polynômes de Chebyshev

Polynôme de Tchebychev

Sommaire

Propriétés des polynômes de Tchebychev de 1re espèce

Propriétés des polynômes de Tchebychev de 2e espèce

Quelques relations avec d'autres fonctions spéciales

Intérêt

Bibliographie

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link

Propriétés des polynômes de Tchebychev de 1^re espèce

Propriétés des polynômes de Tchebychev de 2^e espèce