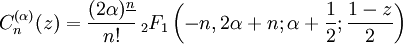Polynome de Gegenbauer
- Polynome de Gegenbauer
-
Polynôme de Gegenbauer
En mathématiques, les polynôme de Gegenbauer ou polynômes ultrasphériques sont une classe de polynômes orthogonaux. Ils sont nommés ainsi en l'honneur de Leopold Gegenbauer (1849 - 1903). Ils sont obtenus à partir des séries hypergéométriques dans les cas où la série est en fait finie :
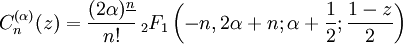
où 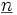 est la factorielle décroissante.
est la factorielle décroissante.
(Voir Abramowitz & Stegun p561)
 Portail des mathématiques
Portail des mathématiques
Catégories : Polynôme remarquable | Fonctions spéciales
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Polynome de Gegenbauer de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Polynôme de gegenbauer — En mathématiques, les polynôme de Gegenbauer ou polynômes ultrasphériques sont une classe de polynômes orthogonaux. Ils sont nommés ainsi en l honneur de Leopold Gegenbauer (1849 1903). Ils sont obtenus à partir des séries hypergéométriques dans… … Wikipédia en Français
Polynôme de Gegenbauer — En mathématiques, les polynôme de Gegenbauer ou polynômes ultrasphériques sont une classe de polynômes orthogonaux. Ils sont nommés ainsi en l honneur de Leopold Gegenbauer (1849 1903). Ils sont obtenus à partir des séries hypergéométriques dans… … Wikipédia en Français
Polynome de Tchebychev — Polynôme de Tchebychev Les polynômes de Tchebychev sont nommés d après le mathématicien Pafnouti Tchebychev. Ils forment une famille de polynômes indexés par les entiers. Le polynôme de Tchebychev (de première espèce) Tn d indice n = 0,1,2,...… … Wikipédia en Français
Polynôme de Tchébychev — Polynôme de Tchebychev Les polynômes de Tchebychev sont nommés d après le mathématicien Pafnouti Tchebychev. Ils forment une famille de polynômes indexés par les entiers. Le polynôme de Tchebychev (de première espèce) Tn d indice n = 0,1,2,...… … Wikipédia en Français
Polynôme de tchebychev — Les polynômes de Tchebychev sont nommés d après le mathématicien Pafnouti Tchebychev. Ils forment une famille de polynômes indexés par les entiers. Le polynôme de Tchebychev (de première espèce) Tn d indice n = 0,1,2,... est uniquement défini par … Wikipédia en Français
Polynôme de Tchebychev — Les polynômes de Tchebychev, nommés ainsi en l honneur du mathématicien russe Pafnouti Lvovitch Tchebychev, constituent deux familles de polynômes (notés pour la première espèce et pour la seconde, l entier naturel n correspondant au degré)… … Wikipédia en Français
Gegenbauer — Gegenbauer, Leopold Bernhard, österreichischer Mathematiker, * Asperhofen (bei Neulengbach) 2. 2. 1849, ✝ Wien 3. 6. 1903; Professor in Tschernowzy (1875 78) und Innsbruck, ab 1893 in Wien; Arbeiten zur Zahlentheorie (u. a. zur Primzahltheorie) … Universal-Lexikon
Gegenbauer-Polynome — Die Gegenbauer Polynome, auch ultrasphärische Polynome sind eine Menge orthogonaler Polynome im Intervall 1..1 mit der Gewichtungsfunktion (1 x2)α 1/2, mit α > 1/2. Sie sind benannt nach dem Mathematiker Leopold Gegenbauer und bilden die… … Deutsch Wikipedia
Gegenbauer-Polynom — Die Gegenbauer Polynome, auch ultrasphärische Polynome , sind eine Menge orthogonaler Polynome im Intervall −1..1 mit der Gewichtungsfunktion (1−x2)α−1/2, mit α > −1/2. Sie sind benannt nach dem Mathematiker Leopold Gegenbauer und bilden die… … Deutsch Wikipedia
Jacobi-Polynome — Die Jacobi Polynome, auch hypergeometrische Polynome sind eine Menge orthogonaler Polynome im Intervall 1..1 mit der Gewichtungsfunktion (1 − z)α(1 + z)β, mit α, β > 1. Sie sind benannt nach dem Mathematiker Carl Gustav Jacob Jacobi und bilden … Deutsch Wikipedia
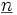 est la factorielle décroissante.
est la factorielle décroissante.