Polygone régulier

Pour les articles homonymes, voir régulier.

Pentagone convexe régulier

En géométrie, un polygone régulier est un polygone équilatéral (tous ses côtés ont la même longueur) dont, de plus, tous les angles ont même mesure. Un polygone régulier est soit un polygone convexe, soit un polygone étoilé (en).

Tous les polygones réguliers convexes d'un même nombre de côtés sont semblables.

Dans certains contextes, tous les polygones considérés seront convexes et réguliers. Dans de telles circonstances, il est d'usage de sous-entendre les deux épithètes « convexe régulier ». Par exemple, toutes les faces des polyèdres uniformes doivent être convexes et régulières et les faces seront décrites simplement en tant que triangle, carré, pentagone...

Plus un polygone convexe a de côtés, plus il tend vers le cercle. Un polygone régulier de 360 côtés a pour angles au centre des angles d'un degré.

De tels polygones sont le support des nombres polygonaux.

Les multiples propriétés des polygones réguliers ont conduit à leur étude mathématique depuis l'Antiquité et à diverses interprétations symboliques, religieuses ou magiques.

Propriétés

Définition équivalente

Une définition équivalente de "polygone régulier" peut être formulée par rotation : si on se donne deux points O et A, un nombre entier n supérieur ou égal à 3, alors les images successives de A par des rotations de centre O et d'angles $\frac{360}{n}^\circ$ génèrent les sommets d'un polygone régulier à n côtés et centre O.

Vocabulaire

Apothème d'un hexagone régulier

Tout polygone régulier est inscrit dans un cercle. Le centre et le rayon de ce cercle sont également appelés centre et rayon du polygone régulier. La distance entre le centre du polygone et chacun des côtés est l'apothème.

Comme les polygones convexes réguliers à n côtés sont semblables, la donnée d'une des trois longueurs (côté, rayon ou apothème) permet de connaître les deux autres et donc de caractériser le polygone.

Si on note h l'apothème, ρ le rayon et c la moitié du côté d'un polygone régulier à n côtés, ces longueurs sont liées par le théorème de Pythagore :

h 2 + c 2 = ρ 2

et par les formules de trigonométrie (les angles étant exprimés en Degrés) suivantes :

$h = \rho\cos\left(\dfrac{180}{n}\right)$

$c = \rho\sin\left(\dfrac{180}{n}\right)$

$c = h\tan\left(\dfrac{180}{n}\right)$

Périmètre et Aire

Si a est la longueur d'un côté, l'aire S et le périmètre P d'un polygone convexe régulier à n côtés est donnée par la formule suivante :

$S = \frac{na^2}{4\tan(\frac{\pi} {n})}\quad\text{et}\quad P = na$

Si ρ désigne le rayon du polygone, c'est-à-dire la distance entre le centre et un sommet, on obtient :

$S = \frac n2 \sin \left(\frac {2\pi}{n}\right)\rho^2 \quad\text{et}\quad P = 2n \sin \left(\frac {\pi}n\right)\rho$

Cette aire est aussi égale à la moitié du périmètre multiplié par la longueur de l'apothème.

Si n est grand, les valeurs π/n et 2π/n deviennent petites, le sinus d'une petite valeur est proche de cette valeur. Plus la valeur est petite, plus la proximité est bonne, on en déduit que plus le nombre de côtés d'un polygone augmente, plus son périmètre et son aire se rapprochent de ceux d'un cercle de même rayon.

Les polygones convexes réguliers ont une propriété remarquable, connue depuis les grecs. Parmi tous les polygones de même nombre de côtés et de même périmètre, celui qui est convexe régulier possède la plus grande aire. Cette aire, toujours plus petite que celle du cercle de même rayon, s'en rapproche au fur et à mesure que n devient plus grand. Ces propriétés sont traitées dans l'article Isopérimétrie.

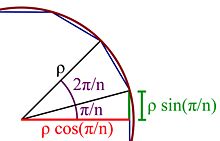
Démonstration

La figure explicative est sur la droite. Pour plus de simplicité, on oriente le polygone de telle manière que l'arête située la plus à droite soit verticale. L'angle associé à une arête est de mesure 2π/n. Il est néanmoins plus simple de considérer les demi-angles, la longueur d'une arête, égale à p/n s'exprime de la manière suivante :

$a = 2\rho \sin \left(\frac {\pi}n\right)\quad\text{et}\quad \rho = \frac a{2\sin \left(\frac {\pi}n\right)}$

La longueur d'une arête est en effet deux fois celle du segment vert sur la figure. La surface S du polygone est la somme des aires de n triangles isocèles, ayant pour hauteur le segment en rouge sur la figure et pour base une arête. Ce qui donne la formule :

$S = n\rho^2 \cos\left(\frac {\pi}n\right)\sin\left(\frac {\pi}n\right)= \frac n2 \sin \left(\frac {2\pi}{n}\right)\rho^2$

En remplaçant ρ par sa valeur, on obtient :

$S = \frac {na^2\cos\left(\frac {\pi}n\right)\sin\left(\frac {\pi}n\right)}{4\sin^2 \left(\frac {\pi}n\right)} = \frac {na^2}{4\tan\left(\frac {\pi}n\right)}$

Apothème et Rayon

L'apothème peut s'exprimer en fonction de la longueur d'un côté a. Elle a alors pour valeur:

$\, h = \frac{a} {2\tan(\frac{\pi} {n})}$

On peut également l'exprimer en fonction de la longueur du rayon ρ. Elle a alors pour valeur:

$\, h = \rho\cos(\frac{\pi} {n})$

Le rayon peut s'exprimer en fonction de la longueur d'un côté a. Il a alors pour valeur:

$\,\rho = \frac{a} {2\sin(\frac{\pi} {n})}$

On peut également l'exprimer en fonction de la longueur de l'apothème h. Il alors pour valeur:

$\, \rho = \frac{h} {\cos(\frac{\pi} {n})}$

Démonstration pour l'apothème et le rayon

On sait que le demi-côté vaut:

$c = h\tan\left(\dfrac{\pi}{n}\right)$

Si a est la longueur d'un côté alors a = 2c. On multiplie donc par 2 et on isole alors h pour trouver son expression:

$\,h = \frac{a} {2\tan(\frac{\pi} {n})}$

On sait que le demi-côté vaut:

$c = \rho\sin\left(\dfrac{\pi}{n}\right)$

Là encore, si a est la longueur d'un côté alors a = 2c. On multiplie donc par 2 et on isole alors ρ pour trouver son expression:

$\,\rho = \frac{a} {2\sin(\frac{\pi} {n})}$

On cherche maintenant à trouver l'expression de l'apothème en fonction du rayon. Pour cela on isole a dans l'équation précedente et on trouve:

$\,a = 2\rho\sin(\frac{\pi} {n})$

On remplace a par l'expression trouvé dans l'équation de l'apothème en fonction du rayon:

$\,h = \frac{2\rho\sin(\frac{\pi} {n})} {2\tan(\frac{\pi} {n})} = \rho\cos(\frac{\pi} {n})$ et donc $\, \rho = \frac{h} {\cos(\frac{\pi} {n})}$

Angles

Pour un polygone convexe régulier à n côtés.

Angle au centre:

Un angle au centre aura pour valeur:

$\,\frac{360}{n}$ degrés.

La somme des angles au centre étant égale au produit d'un angle au centre par le nombre de côtés n, elle sera toujours égale à 360° pour tout polygone convexe régulier.

Angle interne:

Il s'agit de l'angle orienté à partir du sommet commun de deux arêtes consécutives.

Un angle interne aura pour valeur:

$\,(\frac{2n-4} {n})\times 90 = (n-2)\times \frac{180}{n}$ degrés ou $\,\frac{(n-2)\pi}{n}$ radians ou encore $\,\frac{(n-2)}{2n}$ tours.

La somme des angles internes étant égale au produit d'un angle interne par le nombre de côtés n, elle sera égale à $180 n - 360$ degrés. Cette formule est en fait valable pour la somme des angles internes de n'importe quel polygone non croisé, même s'il n'est pas régulier ni même convexe.

Angle externe:

Il s'agit de l'angle opposé à l'angle interne. On obtient sa valeur en soustrayant la valeur de l'angle interne correspondant à 360° pour les dégrés ou à 2π pour les radians ou encore à 2n pour les tours.

Un angle externe aura donc pour valeur:

$\,(\frac{2n+4} {n})\times 90 = (n+2)\times \frac{180}{n}$ degrés ou $\,\frac{(n+2)\pi}{n}$ radians ou encore $\,\frac{(n+2)}{2n}$ tours.

La somme des angles externes étant égale au produit d'un angle externe par le nombre de côtés n, elle sera égale à $180 n + 360$ degrés.

Démonstration pour les angles externes

Pour les dégrés, on soustrait la valeur d'un angle interne en degré à 360°, ce qui donne:

$\,360 -(\frac{2n-4} {n})\times 90 = 360 - \frac{180n-360} {n} = \frac {180n+360} {n} = (\frac{2n+4} {n})\times 90$

Pour les radians, on soustrait la valeur d'un angle interne en radian à 2π, ce qui donne:

$\,2\pi - \frac{(n-2)\pi}{n} = 2\pi - \frac{n\pi - 2\pi} {n} = \frac{n\pi + 2\pi} {n} = \frac{(n + 2)\pi} {n}$

Pour les tours, on soustrait la valeur d'un angle interne en tour à 2n, ce qui donne:

$\,2n - \frac{(n-2)}{2n} = \frac{(n+2)}{2n}$

Valeurs numériques

Côtés	Nom	Aire exacte si a = 1	Demi périmètre si ρ = 1
3	Triangle équilatéral	$\frac {3} {4 \tan (\frac {\pi} {3})} = \frac{\sqrt{3}}{4}$	2,5980762
4	Carré	$\frac {4} {4 \tan (\frac {\pi} {4})} = 1\;$	2.8284271
5	Pentagone régulier	$\frac {5} {4 \tan (\frac {\pi} {5})} = \frac {1}{4} \sqrt{25+10\sqrt{5}}$	2,9389263
6	Hexagone régulier	$\frac {6} {4 \tan (\frac {\pi} {6})} = \frac{3 \sqrt{3}}{2}$	3,000000
7	Heptagone régulier	$\frac {7} {4 \tan (\frac {\pi} {7})}$	3,0371862
8	Octogone régulier	$\frac {8} {4 \tan (\frac {\pi} {8})} = 2 + 2 \sqrt{2}$	3,0614675
9	Ennéagone régulier	$\frac {9} {4 \tan (\frac {\pi} {9})}$	3,0781813
10	Décagone régulier	$\frac {10} {4 \tan (\frac {\pi} {10})} = \frac{5}{2} \sqrt{5+2\sqrt{5}}$	3,0901699
11	Hendécagone régulier	$\frac {11} {4 \tan (\frac {\pi} {11})}$	3,0990581
12	Dodécagone régulier	$\frac {12} {4 \tan (\frac {\pi} {12})} = 6+3\sqrt{3}$	3,1058285
13	Tridécagone régulier	$\frac {13} {4 \tan (\frac {\pi} {13})}$	3,1111036
14	Tétradécagone régulier	$\frac {14} {4 \tan (\frac {\pi} {14})}$	3,1152931
15	Pentadécagone régulier	$\frac {15} {4 \tan (\frac {\pi} {15})}$	3,1186754
16	Hexadécagone régulier	$\frac {16} {4 \tan (\frac {\pi} {16})}$	3,1214452
17	Heptadécagone régulier	$\frac {17} {4 \tan (\frac {\pi} {17})}$	3,1237418
18	Octadécagone régulier	$\frac {18} {4 \tan (\frac {\pi} {18})}$	3,1256672
19	Ennéadécagone régulier	$\frac {19} {4 \tan (\frac {\pi} {19})}$	3,1272972
20	Icosagone régulier	$\frac {20} {4 \tan (\frac {\pi} {20})} = 5 \times \frac {1 + \sqrt{5} + \sqrt{10 - \sqrt{20}}} {1 + \sqrt{5} - \sqrt{10 - \sqrt{20}}}$	3,1286893
30	Triacontagone régulier	$\frac {30} {4 \tan (\frac {\pi} {30})} = \frac {15} {2} \times \frac {\sqrt{15} + \sqrt{3} + \sqrt{10 - \sqrt{20}}} {\sqrt{30 - \sqrt{180}} - \sqrt{5} - 1}$	3,1358539
100	Hectagone régulier	$\frac {100} {4 \tan (\frac {\pi} {100})}$	3,1410759
1 000	Chiliagone régulier	$\frac {1000} {4 \tan (\frac {\pi} {1000})}$	3,1415875
10 000	Myriagone régulier	$\frac {10000} {4 \tan (\frac {\pi} {10000})}$	3,1415926

On remarque que, si le rayon est égal à 1, le demi-périmètre s'approche de plus en plus de π.

Symétrie

Le groupe de symétrie d'un polygone régulier à n-côtés est le groupe diédral (ou diédrique) D_n (d'ordre 2n) : D₂, symétrie rotationnelle d'ordre n), avec les symétries de réflexion par n axes qui passent à travers le centre. Si n est pair, alors la moitié de ces axes passent à travers deux sommets opposés, et l'autre moitié à travers le milieu des côtés opposés. Si n est impair, alors tous les axes passent à travers un sommet et le milieu du côté opposé.

Construction à la règle et au compas

Article détaillé : Construction à la règle et au compas.

Un polygone régulier (convexe ou étoilé) à n arêtes peut être construit avec la règle et le compas si et seulement si les facteurs premiers impairs de n sont des nombres premiers de Fermat distincts, (cf l'article Théorème de Gauss-Wantzel).

Polygones réguliers non convexes

Un pentagramme

Un exemple de polygone régulier étoilé est le pentagramme, qui a les mêmes sommets qu'un pentagone, mais qui est connecté par des sommets alternés.

Les premiers polygones étoilés non composés sont :

Pentagramme - {5/2}
Heptagramme - {7/2}, {7/3}
Octogramme - {8/3}
Ennéagramme - {9/2}, {9/4}
Décagramme - {10/3}

(Voir l'article Stellation)

Polyèdres

Un polyèdre uniforme est un polyèdre avec des polygones réguliers pour faces tels que pour chaque paire de sommet, il existe une isométrie appliquant l'un sur l'autre.Le mot polygone vient du mot poly ( plusieurs) et gone (angles).

Voir aussi

Pavage par des polygones réguliers

Liens externes

Description de polygone régulier avec une animation interactive
Cercle inscrit d'un polygone régulier avec une animation interactive
Aire d'un polygone régulier Trois formules différentes, avec une animation interactive
Géométrie de fleurs avec un polygone régulier Correspondances entre les figures et le tracé des fleurs

v · Polygones
Entre 1 et 10 côtés	Henagone (1) · Digone (2) · Triangle (3) · Quadrilatère (4) · Pentagone (5) · Hexagone (6) · Heptagone (7) · Octogone (8) · Ennéagone (9) · Décagone (10)
Entre 11 et 20 côtés	Hendécagone (11) · Dodécagone (12) · Tridécagone (13) · Tétradécagone (14) · Pentadécagone (15) · Hexadécagone (16) · Heptadécagone (17) · Octadécagone (18) · Ennéadécagone (19) · Icosagone (20)
Entre 21 et 30 côtés	Henicosagone (21) · Doicosagone (22) · Triaicosagone (23) · Tétraicosagone (24) · Pentaicosagone (25) · Hexaicosagone (26) · Heptaicosagone (27) · Octaicosagone (28) · Ennéaicosagone (29) · Triacontagone (30)
Entre 31 et 40 côtés	Hentriacontagone (31) · Dotriacontagone (32) · Tritriacontagone (33) · Tétratriacontagone (34) · Pentatriacontagone (35) · Hexatriacontagone (36) · Heptatriacontagone (37) · Octatriacontagone (38) · Ennéatriacontagone (39) · Tétracontagone (40)
Autres	Pentacontagone (50) · Hexacontagone (60) · Heptacontagone (70) · Octacontagone (80) · Ennéacontagone (90) · Hectogone (100) · Dihectogone (200) · Trihectogone (300) · Tétrahectogone (400) · Pentahectogone (500) · Hexahectogone (600) · Heptahectogone (700) · Octahectogone (800) · Ennéahectogone (900) · Chiliogone (1000) · Myriagone (10000)

Portail de la géométrie

Catégorie :

Polygone

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Polygone régulier de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Polygone regulier — Polygone régulier Pour les articles homonymes, voir régulier. Pentagone régulier En géométrie, il existe deux définitions équivalentes de … Wikipédia en Français
polygone — [ pɔligɔn; pɔligon ] n. m. • 1567; lat. polygonus, gr. polugônos 1 ♦ Figure plane formée par une ligne polygonale fermée. ⇒ quadrilatère, triangle; 1. gone. Côtés, sommets, diagonales d un polygone. Polygone convexe, concave, situé ou non tout… … Encyclopédie Universelle
régulier — régulier, ière [ regylje, jɛr ] adj. et n. m. • 1119 jurs regulers; lat. regularis, de regula « règle » I ♦ (Choses) 1 ♦ (1552) Qui est conforme aux règles, ne fait pas exception à la norme. ⇒ normal. Verbes réguliers, qui suivent les règles… … Encyclopédie Universelle
Polygone equilateral — Polygone équilatéral En géométrie, un polygone équilatéral est un polygone qui a tous ses côtés de même longueur. Un polygone équilatéral qui est convexe et inscrit dans un cercle est un polygone régulier. Un triangle équilatéral est un triangle… … Wikipédia en Français
polygone — POLYGONE. adj. de tout genre. Qui a plusieurs angles. Cette forteresse est de figure polygone. Il est aussi substantif. Un polygone regulier. un polygone irregulier … Dictionnaire de l'Académie française
Polygone — Ne doit pas être confondu avec Polynôme. Pour les articles homonymes, voir Polygone (homonymie). En géométrie euclidienne, un polygone (du grec polus, nombreux, et gônia, angle) est une figure géométrique plane, formée d une suite cyc … Wikipédia en Français
Régulier (géométrie) — Polytope régulier Pour les articles homonymes, voir régulier. Le Dodécaèdre, un des cinq solides platoniciens. E … Wikipédia en Français
Polygone de Pétrie — Pour les articles homonymes, voir Petrie. Le polygone de Pétrie d un octaèdre régulier est de forme hexagonale Un polygone de Pétrie est donné par la projection ort … Wikipédia en Français
POLYGONE — adj. des deux genres T. de Géométrie Qui a plusieurs angles et plusieurs côtés. Une forteresse de forme polygone. On dit plus ordinairement Polygonal. Il s’emploie aussi comme nom masculin. Cette figure est un polygone régulier, un polygone… … Dictionnaire de l'Academie Francaise, 8eme edition (1935)
POLYGONE — adj. des deux genres T. de Géom. Qui a plusieurs angles et plusieurs côtés. Une forteresse de figure polygone. Il est aussi substantif masculin. Cette figure est un polygone régulier, un polygone irrégulier. Les côtés, les angles d un polygone … Dictionnaire de l'Academie Francaise, 7eme edition (1835)

Dictionnaires et Encyclopédies sur 'Academic'

Polygone régulier

Sommaire