- Polygone de Pétrie
-
 Pour les articles homonymes, voir Petrie.
Pour les articles homonymes, voir Petrie. Le polygone de Pétrie d'un octaèdre régulier est de forme hexagonale
Le polygone de Pétrie d'un octaèdre régulier est de forme hexagonale
Un polygone de Pétrie est donné par la projection orthogonale d'un polyèdre (ou même d'un polytope au sens général) sur un plan, de sorte à former un polygone régulier, avec tout le reste de la projection à l’intérieur. Ces polygones et graphes projetés sont utiles pour visualiser la structure et les symétries de polytopes aux nombreuses dimensions.
Chaque paire de côtés consécutifs appartient à une même face du polyèdre, mais pas trois. Cette définition s'étend aux polytopes de dimensions supérieures : chaque groupe de n-1 côtés consécutifs appartient à une même hyperface du polytope, mais pas n.
Le polygone de Pétrie d'un polygone régulier est lui-même, car il est déjà dans le plan de projection.
Sommaire
Histoire
John Flinders Petrie était le seul fils de Sir William Matthew Flinders Petrie, le grand égyptologue. Il est né en 1907, et montra à l'école de remarquables aptitudes en mathématiques[1]. En se concentrant il pouvait répondre aux questions sur des objets quadridimensionnels en les visualisant dans sa tête.
Il fut le premier à réaliser l'importance des polygones visibles seulement sous un certain angle par transparence, et dont les sommets n'étaient pas coplanaires, sur la surface des polyèdres et des polytopes des dimensions au dessus. Il fut un grand ami de Coxeter, qui nomma ces polygones en son honneur. L'idée des polygones de Petrie a été étendue bien plus tard aux polytopes semi-réguliers.
En 1972, quelques mois après sa retraite, Petrie a été tué par une voiture alors qu'il essayait de traverser une grande route à côté de sa maison dans le Surrey.
Polygones de Pétrie des polyèdres réguliers
Il y a 5 polyèdres réguliers (voir solide de Platon). Le polygone de Pétrie d'un polyèdre régulier {p,q} (voir symbole de Schläfli) possède h côtés, où :

Les polyèdres duaux (voir dualité), {p,q} et {q,p}, sont donc contenus par les mêmes polygones de Pétrie.
Polygones de Pétrie pour les Polyèdres réguliers (en rouge) 
tétraèdre cube octaèdre dodécaèdre icosaèdre 
























centré sur une arête centré sur un sommet centré sur une face centré sur une face centré sur un sommet 4 côtés 6 côtés 6 côtés 10 côtés 10 côtés V:(4,0) V:(6,2) V:(6,0) V:(10,10,0) V:(10,2) Les polygones de Pétrie sont les bords (en rouge) de ces projections orthogonales. Les lignes bleues représentent les arêtes de devant, et les lignes noires les arêtes de derrière.
Les sommets, qui sont sur des cercles concentriques, sont comptés par "couches" à partir de l'extérieur jusqu'à l'intérieur, par la notation du polygone de Pétrie : V:(a,b,...) avec un 0 à la fin si la couche centrale est vide.
Polygones de Pétrie des polytopes réguliers de dimensions supérieures
Les polygones de Pétrie pour les polychores réguliers (voir 4-polytope régulier convexe) {p,q,r} (voir symbole de Schläfli) peuvent également être déterminés.
Les polychores duaux (voir dualité), {p,p,q} et {p,q,q}, sont contenus par les mêmes polygones de Pétrie.
Polygones de Pétrie des 6 polychores réguliers (polytopes réguliers à 4 dimensions) 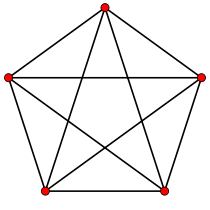
{3,3,3}







pentachore (4-simplexe)
5 côtés
V:(5,0)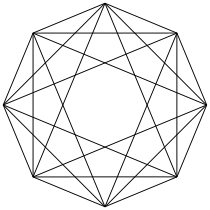
{3,3,4}







hexadécachore (4-hyperoctaèdre)
8 côtés
V:(8,0)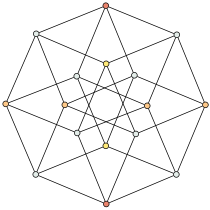
{4,3,3}







tesseract (4-hypercube)
8 côtés
V:(8,8,0)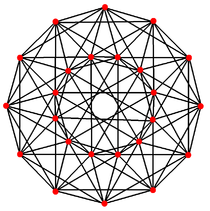
{3,4,3}







24-cellules
12 côtés
V:(12,6,6,0)
{5,3,3}







120-cellules
30 côtés
V:((30,60)3,603,30,60,0)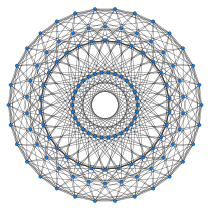
{3,3,5}







600-cellules
30 côtés
V:(30,30,30,30,0)
Ensuite, comme l'a démontré Ludwig Schläfli, il n'y a pas plus de 3 polytopes réguliers par dimension, et cela dès la cinquième. Ces trois n-polytopes réguliers appartiennent respectivement à 3 grandes familles de polytopes : les n-simplexes, les hyperoctaèdres, et les hypercubes.Le polygone de Pétrie pour un polytope régulier {p, q ,r ,..., w} peut aussi être déterminé.
La famille des simplexes
Dans la famille des simplexes, tout n-simplexe est projeté dans un polygone à n+1 côtés, avec les sommets à la périphérie.
Pour un simplexe, toutes les diagonales du polygone de Pétrie sont tracées.
Les simplexes sont des polytopes auto-duaux : chaque simplexe est son propre dual, car la permutation des 3 de sa notation de Schläfli {3,3,3,...,3} est invariante.
Polygones de Pétrie des n-simplexes n = 1
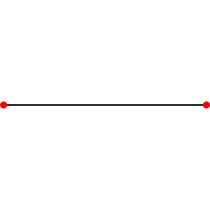
{}

segment
1-simplexe
2 côtés (le segment est alors considéré en tant que digone)
V:(2,0)n = 2
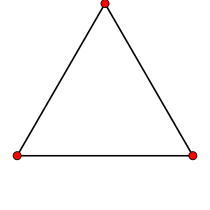
{3}



triangle
2-simplexe
3 côtés
V:(3,0)n = 3
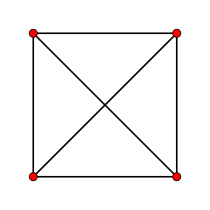
{3,3}





tétraèdre
3-simplexe
4 côtés
V:(4,0)n = 4

{33}







Pentachore
4-simplexe
5 côtés
V:(5,0)n = 5
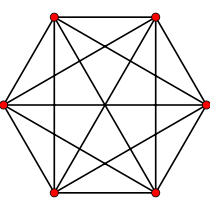
{34}









5-simplexe
6 côtés
V:(6,0)n = 6
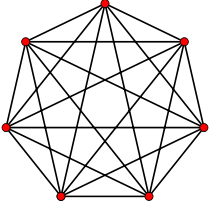
{35}











6-simplexe
7 côtés
V:(7,0)n = 7
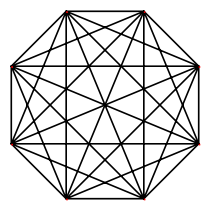
{36}












7-simplexe
8 côtés
V:(8,0)n = 8
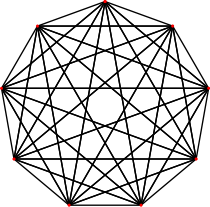
{37}















8-simplexe
9 côtés
V:(9,0)n = 9
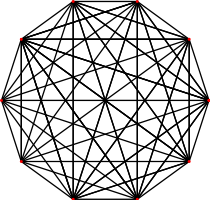
{38}

















9-simplexe
10 côtés
V:(10,0)n = 10
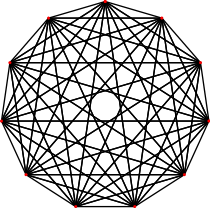
{39}



















10-simplexe
11 côtés
V:(11,0)La famille des hypercubes
Dans la famille des hypercubes, tout n-hypercube est projeté dans un polygone à 2n côtés.
Les duaux respectifs des hypercubes {4,3,3,3,...,3} sont les hyperoctaèdres {3,3,3,...,3,4}.
Polygones de Pétrie des hypercubes n = 1

{}

segment (digone)
2 côtés
V:(2,0)n=2
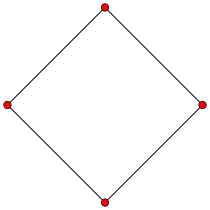
{4}



carré
4 côtés
V:(4,0)n = 3
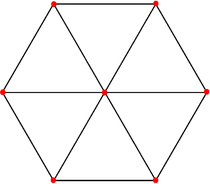
{4,3}





cube
6 côtés
V:(6,2)n = 4

{4,32}







tesseract
8 côtés
V:(8,8,0)n = 5
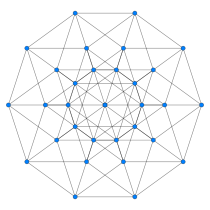
{4,33}









penteract
10 côtés
V:(10,10,10,2)n = 6
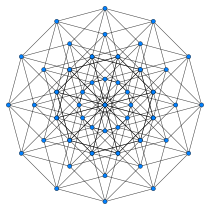
{4,34}









hexéract
12 côtésn = 7
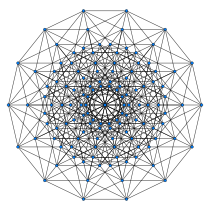
{4,35













heptéract
14 côtésn = 8
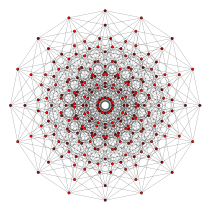
{4,36}















octéract
16 côtésn = 9

{4,37}

















ennéract
18 côtésn = 10
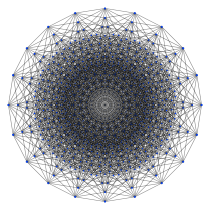
{4,38}



















décaract
20 côtésLa famille des hyperoctaèdres
Dans la famille des hyperoctaèdres, tout n-octaèdre est projeté dans un polygone de Pétrie à 2n côtés.
Les duaux respectifs des hyperoctaèdres {3,3,3,...,3,4} sont les hypercubes {4,3,3,3,...,3}.
Polygones de Pétrie des hyperoctaèdres n = 1

{}

2 côtés
V:(2,0)n = 2

{4}



carré
4 côtés
V:(4,0)n = 3
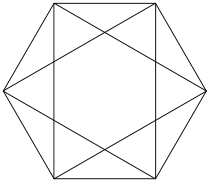
{3,4}





octaèdre
6 côtés
V:(6,0)n = 4

{32,4}







16-cellules
8 côtés
V:(8,0)n = 5
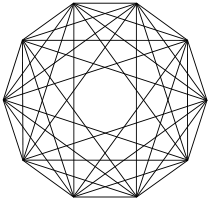
{33,4}









penta-croisé
10 côtés
V:(10,0)n = 6
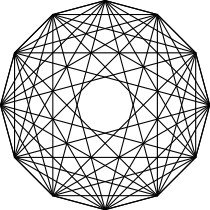
{34,4}











hexa-croisé
12 côtés
V:(12,0)n = 7
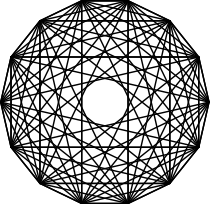
{35,4}













hepta-croisé
14 côtés
V:(14,0)n = 8
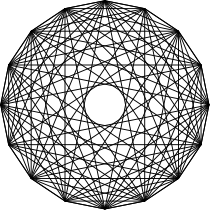
{36,4}















octa-croisé
16 côtés
V:(16,0)n = 9
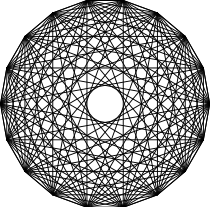
{37,4}

















ennéa-croisé
18 côtés
V:(18,0)n = 10
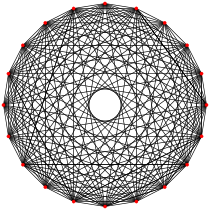
{38,4}



















déca-croisé
20 côtés
V:(20,0)Notes et références
Voir aussi
Articles connexes
- Théorie des graphes
- Polygone régulier
- Solide de Platon
- Hypercube, simplexe, hyperoctaèdre, polychore régulier
- Projection (géométrie)
Bibliographie
- Coxeter, H. S. M. The Beauty of Geometry: Twelve Essays (1999), Dover Publications (ISBN 978-0-486-40919-1)
- Coxeter, H.S.M.; Regular complex polytopes (1974). Section 4.3 Flags and Orthoschemes, Section 11.3 Petrie polygons
- Coxeter, H. S. M. Petrie Polygons. Regular Polytopes, 3rd ed. New York: Dover, 1973. (sec 2.6 Petrie Polygons pp. 24–25, and Chapter 12, pp. 213-235, The generalized Petrie polygon )
- Coxeter, H.S.M.; Regular complex polytopes (1974).
Liens externes
Sur Mathworld (en anglais) :
Wikimedia Foundation. 2010.
