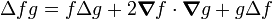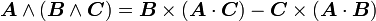Opérateurs nabla dans les coordonnées cylindriques et sphériques

Opérateurs nabla dans les coordonnées cylindriques et sphériques

Nabla

Articles d'analyse vectorielle
Champ vectorielChamp scalaire
Objets d'étude
Champ vectoriel Champ scalaire
Équation aux dérivées partielles
de Laplace de Poisson
Opérateurs
Nabla Gradient
Rotationnel Divergence
Laplacien scalaire Bilaplacien
Laplacien vectoriel D'alembertien
Théorèmes
de Green de Stokes
de Helmholtz de flux-divergence
du gradient du rotationnel

Nabla, noté \nabla, est un symbole mathématique pouvant aussi bien désigner le gradient d'une fonction en analyse qu'une connexion de Koszul en géométrie différentielle. Les deux notions sont évidemment reliées, ce qui explique l'utilisation d'un même symbole. En physique, il est utilisé de manière informelle en dimension 3 pour représenter aisément la divergence (∇·A), le rotationnel (∇∧A) et le laplacien vectoriel (ΔA = ∇2A) d'un champ vectoriel A, ainsi que le gradient (∇f) et le laplacien (Δf = ∇2f) d'un champ scalaire f. Ces notions sont fondamentales en physique, notamment en électromagnétisme et en hydrodynamique.

Sommaire

Origine historique

La forme de Nabla vient de la lettre grecque delta majuscule (Δ) renversée, à cause d'une utilisation comparable, la lettre grecque à l'endroit étant déjà utilisée pour désigner un opérateur (le laplacien) en calcul différentiel. Le nabla a été introduit par Peter Guthrie Tait en 1867. D'abord surnommé avec malice « atled » (delta à l'envers) par James Maxwell, le nom Nabla lui fut donné par Tait sur l'avis de William Robertson Smith, en 1870, par analogie de forme avec une harpe grecque qui dans l'antiquité portait ce nom.

Formulaire d'analyse vectorielle

Ceci est une liste de quelques formules d'analyse vectorielle d'emploi général en travaillant avec plusieurs systèmes de coordonnées communs.

Opération Coordonnées cartésiennes (x,y,z) Coordonnées cylindriques (ρ,φ,z) Coordonnées sphériques (r,θ,φ)
Définition
des
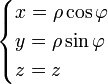
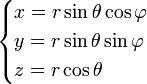
coordonnées		 \begin{cases} x = \rho\cos\varphi \\ y = \rho\sin\varphi \\ z = z \end{cases} \begin{cases} x = r\sin\theta\cos\varphi \\ y = r\sin\theta\sin\varphi \\ z = r\cos\theta \end{cases}
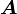
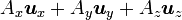
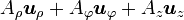
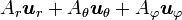
\boldsymbol A A_x \boldsymbol u_x + A_y \boldsymbol u_y + A_z \boldsymbol u_z A_\rho \boldsymbol u_\rho + A_\varphi \boldsymbol u_\varphi + A_z \boldsymbol u_z A_r \boldsymbol u_r + A_\theta \boldsymbol u_\theta + A_\varphi \boldsymbol u_\varphi
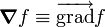
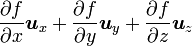
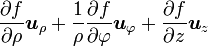
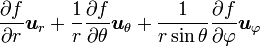
\boldsymbol \nabla f \equiv \overrightarrow{\mathrm{grad}} f {\partial f \over \partial x}\boldsymbol u_x + {\partial f \over \partial y}\boldsymbol u_y + {\partial f \over \partial z}\boldsymbol u_z {\partial f \over \partial \rho}\boldsymbol u_\rho + {1 \over \rho}{\partial f \over \partial \varphi}\boldsymbol u_\varphi + {\partial f \over \partial z}\boldsymbol u_z {\partial f \over \partial r}\boldsymbol u_r + {1 \over r}{\partial f \over \partial \theta}\boldsymbol u_\theta + {1 \over r\sin\theta}{\partial f \over \partial \varphi}\boldsymbol u_\varphi
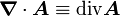
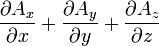
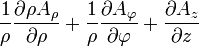
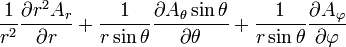
\boldsymbol \nabla\cdot\boldsymbol A \equiv \mathrm{div} \boldsymbol A {\partial A_x \over \partial x} + {\partial A_y \over \partial y} + {\partial A_z \over \partial z} {1 \over \rho}{\partial \rho A_\rho \over \partial \rho} + {1 \over \rho}{\partial A_\varphi \over \partial \varphi} + {\partial A_z \over \partial z} {1 \over r^2}{\partial r^2 A_r \over \partial r} + {1 \over r\sin\theta}{\partial A_\theta\sin\theta \over \partial \theta} + {1 \over r\sin\theta}{\partial A_\varphi \over \partial \varphi}
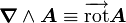
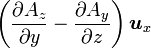
\boldsymbol \nabla \wedge \boldsymbol A \equiv \overrightarrow{\mathrm{rot}} \boldsymbol A \left({\partial A_z \over \partial y} - {\partial A_y \over \partial z}\right) \boldsymbol u_x

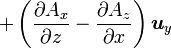
+ \left({\partial A_x \over \partial z} - {\partial A_z \over \partial x}\right) \boldsymbol u_y
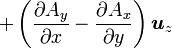
+ \left({\partial A_y \over \partial x} - {\partial A_x \over \partial y}\right) \boldsymbol u_z

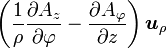
\left({1 \over \rho}{\partial A_z \over \partial \varphi} - {\partial A_\varphi \over \partial z}\right) \boldsymbol u_\rho

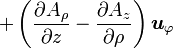
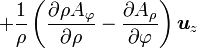
+ \left({\partial A_\rho \over \partial z} - {\partial A_z \over \partial \rho}\right) \boldsymbol u_\varphi + {1 \over \rho}\left({\partial \rho A_\varphi \over \partial \rho} - {\partial A_\rho \over \partial \varphi}\right) \boldsymbol u_z

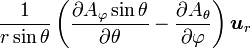
{1 \over r\sin\theta}\left({\partial A_\varphi\sin\theta \over \partial \theta} - {\partial A_\theta \over \partial \varphi}\right) \boldsymbol u_r

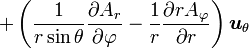
+ \left({1 \over r\sin\theta}{\partial A_r \over \partial \varphi} - {1 \over r}{\partial r A_\varphi \over \partial r}\right) \boldsymbol u_\theta
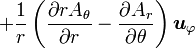
+ {1 \over r}\left({\partial r A_\theta \over \partial r} - {\partial A_r \over \partial \theta}\right) \boldsymbol u_\varphi

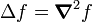
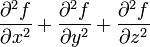
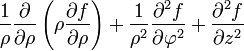
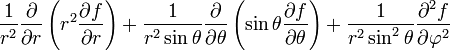
\Delta f = \boldsymbol \nabla^2 f {\partial^2 f \over \partial x^2} + {\partial^2 f \over \partial y^2} + {\partial^2 f \over \partial z^2} {1 \over \rho}{\partial \over \partial \rho}\left(\rho {\partial f \over \partial \rho}\right) + {1 \over \rho^2}{\partial^2 f \over \partial \varphi^2} + {\partial^2 f \over \partial z^2} {1 \over r^2}{\partial \over \partial r}\left(r^2 {\partial f \over \partial r}\right) + {1 \over r^2\sin\theta}{\partial \over \partial \theta}\left(\sin\theta {\partial f \over \partial \theta}\right) + {1 \over r^2\sin^2\theta}{\partial^2 f \over \partial \varphi^2}
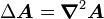
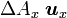
\Delta \boldsymbol A = \boldsymbol \nabla^2 \boldsymbol A \Delta A_x \; \boldsymbol u_x

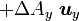
+ \Delta A_y \; \boldsymbol u_y
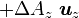
+ \Delta A_z \; \boldsymbol u_z

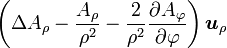
 \left(\Delta A_\rho - {A_\rho \over \rho^2} - {2 \over \rho^2}{\partial A_\varphi \over \partial \varphi}\right) \boldsymbol u_\rho

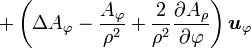
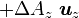
+ \left(\Delta A_\varphi - {A_\varphi \over \rho^2} + {2 \over \rho^2}{\partial A_\rho \over \partial \varphi}\right)\boldsymbol u_\varphi + \Delta A_z \; \boldsymbol u_z

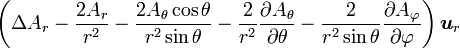
 \left(\Delta A_r - \frac{2 A_r}{r^2} - \frac{2 A_\theta\cos\theta}{r^2\sin\theta} - \frac{2}{r^2} \frac{\partial A_\theta}{\partial \theta} - \frac{2}{r^2\sin\theta}\frac{\partial A_\varphi}{\partial \varphi}\right) \boldsymbol u_r

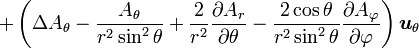
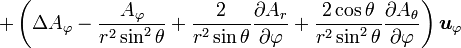
+\left(\Delta A_\theta - \frac{A_\theta}{r^2\sin^2\theta} + \frac{2}{r^2}\frac{\partial A_r}{\partial \theta} - \frac{2 \cos\theta}{r^2\sin^2\theta}\frac{\partial A_\varphi}{\partial \varphi}\right) \boldsymbol u_\theta +\left(\Delta A_\varphi - \frac{A_\varphi}{r^2\sin^2\theta} + \dfrac{2}{r^2\sin\theta}\frac{\partial A_r}{\partial \varphi} + \frac{2 \cos\theta}{r^2\sin^2\theta}\frac{\partial A_\theta}{\partial \varphi}\right) \boldsymbol u_\varphi
Quelques autres règles de calcul
\operatorname{div}\ \overrightarrow{\operatorname{grad}} f = \boldsymbol \nabla \cdot (\boldsymbol \nabla f) = \boldsymbol \nabla^2 f = \Delta f (laplacien)
\overrightarrow{\operatorname{rot}}\ \overrightarrow{\operatorname{grad}} f = \boldsymbol \nabla \wedge (\boldsymbol \nabla f) = \boldsymbol 0
\operatorname{div}\ \overrightarrow{\operatorname{rot}} \; \boldsymbol A = \boldsymbol \nabla \cdot (\boldsymbol \nabla \wedge \boldsymbol A) = 0
\overrightarrow{\operatorname{rot}}\ \overrightarrow{\operatorname{rot}} \; \boldsymbol A = \boldsymbol \nabla \wedge (\boldsymbol \nabla \wedge \boldsymbol A) = \boldsymbol \nabla (\boldsymbol \nabla \cdot \boldsymbol A) - \boldsymbol \nabla^2 \boldsymbol A = \overrightarrow{\operatorname{grad}}\ \operatorname{div} \boldsymbol A - \Delta \boldsymbol A (rotationnel du rotationnel)
\Delta f g = f \Delta g + 2 \boldsymbol \nabla f \cdot \boldsymbol \nabla g + g \Delta f

Formule de Lagrange pour le produit vectoriel

\boldsymbol A \wedge (\boldsymbol B \wedge \boldsymbol C) = \boldsymbol B \times (\boldsymbol A \cdot \boldsymbol C) - \boldsymbol C \times (\boldsymbol A \cdot \boldsymbol B)
Table avec les \nabla (nabla ou del) dans les coordonnées cylindriques ou sphériques

Ces opérateurs ne sont pas de produits scalaires, mais bien d'applications, malgré la notation ambiguë 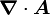\boldsymbol \nabla \cdot \boldsymbol A. Le résultat est le même pour les coordonnées cartésiennes, mais devient faux pour les coordonnées curvilignes quelconques.

Voir aussi

Articles connexes

Liens externes

  • Portail des mathématiques Portail des mathématiques
  • Portail de la physique Portail de la physique
Ce document provient de « Nabla ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Opérateurs nabla dans les coordonnées cylindriques et sphériques de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Nabla — Nabla, noté , est un symbole mathématique pouvant aussi bien désigner le gradient d une fonction en analyse qu une connexion de Koszul en géométrie différentielle. Les deux notions sont évidemment reliées, ce qui explique l utilisation d un même… …   Wikipédia en Français

  • Analyse Vectorielle — Articles d analyse vectorielle …   Wikipédia en Français

  • Analyse vectorielle — L analyse vectorielle est une branche des mathématiques qui étudie les champs de scalaires et de vecteurs suffisamment réguliers des espaces euclidiens, c est à dire les applications différentiables d un ouvert d un espace euclidien E à valeurs… …   Wikipédia en Français

  • Calcul vectoriel — Analyse vectorielle Articles d analyse vectorielle …   Wikipédia en Français

  • Coordonnees spheriques — Coordonnées sphériques Un point repéré en coordonnées sphériques Les coordonnées sphériques sont un système de coordonnées de l espace qui généralise les coordonnées polaires du plan. Un point de l espace y est repéré par la distance à un pôle et …   Wikipédia en Français

  • Coordonnées Sphériques — Un point repéré en coordonnées sphériques Les coordonnées sphériques sont un système de coordonnées de l espace qui généralise les coordonnées polaires du plan. Un point de l espace y est repéré par la distance à un pôle et deux angles, le… …   Wikipédia en Français

  • Coordonnées sphériques — En coordonnées sphériques, la position du point P est définie par la distance ρ et par les angles θ et Φ. On appelle coordonnées sphériques divers systèmes de coordonnées de l espace qui généralisent les coordonnées polaires du plan. Un point de… …   Wikipédia en Français

  • ∇ — Nabla Articles d analyse vectorielle Objets d étude …   Wikipédia en Français

  • Systeme de coordonnees — Système de coordonnées Pour les articles homonymes, voir Système de coordonnées (homonymie). En mathématiques, un système de coordonnées permet de faire correspondre à chaque point d un espace à N dimensions, un N uplet de scalaires. Dans… …   Wikipédia en Français

  • Système de coordonnées — Pour les articles homonymes, voir Système de coordonnées (homonymie). En mathématiques, un système de coordonnées permet de faire correspondre à chaque point d un espace à N dimensions, un N uplet de scalaires. Dans beaucoup de cas, les scalaires …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”