Coordonnées sphériques

En coordonnées sphériques, la position du point P est définie par la distance ρ et par les angles θ et Φ.

On appelle coordonnées sphériques divers systèmes de coordonnées de l'espace qui généralisent les coordonnées polaires du plan. Un point de l'espace y est repéré par la distance à un pôle et deux angles. Ce système est d'emploi courant pour le repérage géographique : l'altitude, la latitude, et la longitude sont une variante de ces coordonnées. Plusieurs systèmes de coordonnées sphériques sont également employés en astrométrie.

Il existe différentes conventions concernant la définition des angles. Cet article utilise la convention P(ρ,φ,θ), utilisée en mathématiques, où φ désigne la colatitude et est compris entre 0 et π, et θ désigne la longitude et est compris entre 0 et 2π.

Sommaire

1 Histoire
2 Définition et propriétés élémentaires
- 2.1 Conventions
- 2.2 Lien avec les coordonnées polaires
3 Utilisation
4 Propriétés
- 4.1 Propriétés différentielles
- 4.2 Relation avec les autres systèmes de coordonnées usuels
5 Généralisation
6 Sources

Histoire

Article détaillé : histoire des fonctions trigonométriques.

Définition et propriétés élémentaires

Conventions

rayon-colatitude-longitude

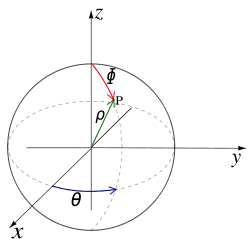
coordonnées sphériques (ρ, ϕ, θ) d'un point dans un repère cartésien (O, x, y, z).

Étant donné un repère cartésien (O, x, y, z), les coordonnées sphériques (ρ, ϕ, θ) d'un point P sont définies par :

ρ est la distance du point P au centre O ;
ϕ est l'angle non orienté formé par les vecteurs z et OP, appelé angle zénithal ou colatitude ;
θ est l'angle orienté formé par les demi-plans ayant pour frontière l'axe vertical et contenant respectivement la demi-droite [O, x) et le point P. Si H est le projeté orthogonal de P dans le plan horizontal (O, x,y), alors θ peut être défini comme l'angle formé par les vecteurs x et OH.

Par convention, et pour assurer l'unicité pour ρ > 0, ϕ est compris entre 0 et π radians (0 et 180°) et θ entre 0 et 2π radians (0 et 360°)^[1] (pour le repérage, mais θ et ϕ peuvent parcourir un intervalle plus important pour une courbe paramétrée ρ(θ, ϕ) ). En conséquence la relation de passage aux coordonnées cartésiennes s'écrit :

$\begin{cases} x &= \rho \cos \theta \sin \phi \\ y &= \rho \sin \theta \sin \phi \\ z &= \rho \cos \phi \end{cases}$

On utilise cette notation dans la suite de l'article.

rayon-colatitude-longitude

En physique, les notations ϕ et θ sont généralement interverties^[1], conformément au standard ISO 31-11 sur les « signes et symboles mathématiques à utiliser en sciences physiques et en technologie »^[2]. La distance au pôle est souvent notée r^[1].

Un point repéré en coordonnées sphériques (rayon/longitude/latitude) ; ici la latitude est noté d'un δ

rayon-longitude-latitude

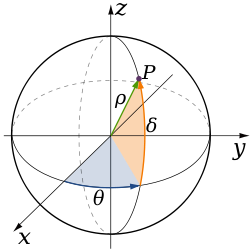
En mathématiques, on emploie également le système des géographes : on nomme les coordonnées (ρ, θ, δ), où ρ désigne toujours la distance du point au pôle, alors que θ désigne cette fois la longitude (angle mesuré depuis l'axe des x et généralement entre -180° et 180°) et δ la latitude, l'angle depuis le plan équatorial (entre -90° et 90°). L'échange entre les coordonnées cartésiennes et les coordonnées sphériques se fait alors par les formules :

$\begin{cases} x &= \rho \cos \theta \cos \delta \\ y &= \rho \sin \theta \cos \delta \\ z &= \rho \sin \delta \end{cases}$

Il est aisé de passer d'un système à un autre car latitude et colatitude sont liées par

δ = 90 - ϕ

Lien avec les coordonnées polaires

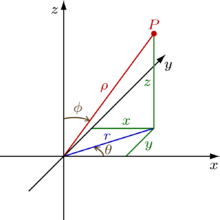
Article détaillé : coordonnées polaires.

Dans le plan vertical (O, z, OP), le système de coordonnées ( $ρ$ , $Φ$ ) est polaire. Dans le plan horizontal (O, x, y), ( $ρ$ $sin Φ$ , $θ$ ) est aussi un système de coordonnées polaires.

Soit $\overrightarrow{r} = \overrightarrow{OP}$

$\phi = (\overrightarrow{Oz},\overrightarrow{OP})$

$P'$ le projeté de $P$ sur le plan $x O y$

$\overrightarrow{OP'} = \overrightarrow{r} \sin(\phi)$

$\theta = (\overrightarrow{Ox},\overrightarrow{OP'})$

Les coordonnées cartésiennes du point P sont : $\left\{ \begin{matrix} z &=& \rho \cos\phi&&\\ x &=& OP' \cos\theta &=& \rho \sin\phi\cos\theta\\ y &=& OP' \sin \theta &=& \rho \sin\phi\sin\theta \end{matrix} \right.$

Utilisation

Repérage géographique

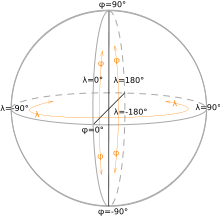
Coordonnées géographiques φ (latitude) et λ (longitude).

Articles détaillés : coordonnées géographiques et géoïde.

Les coordonnées géographiques, utilisées pour se repérer sur la surface de la Terre, sont une variante des coordonnées sphériques. Elles utilisent les coordonnées h (altitude), l (latitude) et λ (longitude), qui sont reliées aux coordonnées sphériques par :

$\begin{align} h &= \rho - \rho_\text{g}(l, \lambda),\\ l &= 90^\text{o} - \phi,\\ \lambda &= \theta \text{ si } \theta \le 180^\text{o}\\ &= \theta-360 \text{ sinon}, \end{align}$

où ρ_g(l, λ) est la distance au centre de la Terre du point du géoïde situé dans la direction (l, λ). Lorsque l'ellipsoïde de révolution est utilisé à la place du géoïde, h est alors la hauteur géodésique ou hauteur ellipsoïdale, encore nommée hauteur au-dessus de l'ellipsoïde; elle diffère de l'altitude d'environ +/-100 m au plus. La hauteur ellipsoïdale est une grandeur purement géométrique, l'altitude est une grandeur physique. La grandeur h est la distance mesurée le long de la normale à l'ellipsoïde entre ce dernier et le point considéré.

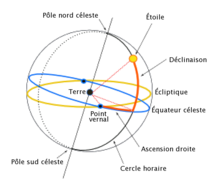
Coordonnées célestes

Coordonnées équatoriales : déclinaison et ascension droite.

Article détaillé : coordonnées célestes.

Les coordonnées célestes, utilisées pour repérer les astres sur le ciel, utilisent cette même variante avec ρ fixé (projection sur la voûte céleste). Par exemple, le système de coordonnées équatoriales, utilisé pour repérer les objets hors du système solaire, utilisent la déclinaison (correspond à l) et l'ascension droite (correspond à λ, exprimée en heures, avec 1 h = 15°).

Calculs

Les coordonnées sphériques sont d'emploi courant dans trois cas :

mouvement à distance fixe d'un point donné, comme dans le cas d'un pendule ;
mouvement à force centrale, notamment dans le potentiel de Coulomb;
problèmes présentant une symétrie sphérique.

Exemple du pendule

Article détaillé : pendule.

Exemple de l'attraction coulombienne

Articles détaillés : équation de Schrödinger et harmonique sphérique.

Propriétés

Propriétés différentielles

Différentielles

Le volume infinitésimal s'écrit

$\text{d}^3 V = \rho^2\sin\phi\,\text{d}\rho\text{d}\phi\text{d}\theta$

et la surface à ρ constant est $\text{d}^2 S = \rho^2\sin\phi\,\text{d}\phi\text{d}\theta$ .

Les vecteurs de la base comobile $(\overrightarrow{u_\rho}, \overrightarrow{u_\phi}, \overrightarrow{u_\theta})$ ont pour différentielles :

$\begin{align} \text{d}\overrightarrow{u_\rho} &= + \text{d}\phi\,\vec{u}_\phi + \sin\phi\,\text{d}\theta\,\vec{u}_\theta,\\ \text{d}\overrightarrow{u_\phi} &= -\text{d}\phi\,\vec{u}_\rho + \cos\phi\,\text{d}\theta\,\vec{u}_\theta,\\ \text{d}\overrightarrow{u_\theta} &= -\sin\phi\,\text{d}\theta\,\vec{u}_\rho - \cos\phi\,\text{d}\theta\,\vec{u}_\phi. \end{align}$

Cinématique

Les quantités cinématiques, position, vitesse et accélération s'en déduisent :

$\begin{align} \overrightarrow{OM} &= \rho\,\overrightarrow{u_\rho},\\ \dot{\overrightarrow{OM}} &= \dot\rho\,\overrightarrow{u_\rho} + \rho\dot\phi\,\overrightarrow{u_\phi} + \rho\sin\phi\,\dot\theta\,\overrightarrow{u_\theta},\\ \ddot{\overrightarrow{OM}} &= (\ddot\rho-\rho\dot\phi^2-\rho\dot\theta^2\sin^2\phi)\,\overrightarrow{u_\rho} + (\rho\ddot\phi + 2\dot\rho\dot\phi - \rho\dot\theta^2\sin \phi\,\cos\phi) \,\overrightarrow{u_\phi} + (\rho\ddot\theta\sin\phi + 2\dot\rho\dot\theta\sin\phi + 2\rho\dot\phi\dot\theta\cos \phi) \,\overrightarrow{u_\theta}. \end{align}$

Opérateurs différentiels

Article détaillé : nabla.

L'opérateur nabla, servant au calcul du gradient, de la divergence et du rotationnel s'écrit

$\overrightarrow{u_\nabla} = \left(\frac\partial{\partial\rho}, \frac1\rho \frac\partial{\partial\phi}, \frac1{\rho\sin\phi} \frac\partial{\partial\theta}\right).$

Le laplacien s'en déduit :

$\Delta = \frac1{\rho^2} \frac\partial{\partial\rho}\left(\rho^2\frac\partial{\partial\rho}\right) +\frac1{\rho^2\sin\phi} \frac\partial{\partial\phi}\left(\sin\phi\frac\partial{\partial\phi}\right) +\frac1{\rho^2\sin^2\phi} \frac{\partial^2}{\partial\theta^2}.$

Tenseurs usuels

Articles détaillés : tenseur métrique et symbole de Christoffel.

Le tenseur métrique s'écrit

$g_{ij} = \left(\begin{matrix} 1 & 0 & 0\\ 0 & \rho^2 & 0\\ 0 & 0 & \rho^2 \sin^2\phi \end{matrix}\right)$

et l'intervalle

$\text{d}s^2 = c^2\text{d}t^2 - \text{d}\rho^2 - \rho^2\text{d}\phi^2 - \rho^2\sin^2\phi\,\text{d}\theta^2.$

Les éléments non nuls du symbole de Christoffel sont

$\begin{align} \Gamma^{\rho}_{\phi\phi} &= -\rho\\ \Gamma^{\rho}_{\theta\theta} &= -\rho \sin^2\phi\\ \Gamma^{\phi}_{\rho\phi} = \Gamma^{\phi}_{\phi\rho} &= \rho^{-1}\\ \Gamma^{\phi}_{\theta\theta} &= -\cos\phi\,\sin\phi\\ \Gamma^{\theta}_{\rho\theta} = \Gamma^{\theta}_{\theta\rho} &= \rho^{-1}\\ \Gamma^{\theta}_{\theta\phi} = \Gamma^{\theta}_{\phi\theta} &= \cot\phi \end{align}$

Relation avec les autres systèmes de coordonnées usuels

Les coordonnées cartésiennes (x, y, z), cylindriques (r, θ′, z) et sphériques, lorsqu'elles sont définies par rapport au même repère cartésien (O, x, y, z) suivent les lois de transformations données ci-dessous.

Système de coordonnées	Depuis les coordonnées sphériques	Vers les coordonnées sphériques
Coordonnées cartésiennes	$\begin{align} x &= \rho \sin\phi \cos\theta,\\ y &= \rho \sin\phi \sin\theta,\\ z &= \rho \cos\phi. \end{align}$	$\begin{align} \rho &= \sqrt{x^2+y^2+z^2},\\ \phi &= \arccos(z/\rho)\\ \theta &= \begin{cases}\arccos\frac{x}{\sqrt{x^2+y^2}} & \mathrm{si}\ y\geq0, \\[,5em] 2\pi-\arccos\frac x{\sqrt{x^2+y^2}} & \mathrm{si}\ y < 0;\end{cases} \end{align}$
Coordonnées cylindriques	$\begin{align} r &= \rho \sin\phi,\\ \theta^\prime &= \theta,\\ z &= \rho \cos\phi. \end{align}$	$\begin{align} \rho &= \sqrt{r^2+z^2},\\ \phi &= \arctan(r/z),\\ \theta &= \theta^\prime, \end{align}$

Dans le tableau ci-dessus arctan(y, x) est le prolongement classique sur les différents quadrants de arctan(y/x) pour x et y positifs.

Coordonnées sphériques
Coordonnées cartésiennes
Coordonnées cylindriques

Cliquez sur une vignette pour l’agrandir

Généralisation

Article détaillé : 3-sphère#Coordonnées hypersphériques.

Soit un espace vectoriel normé de dimension n finie. Pour un point x de cet espace, de coordonnées (x₁, …, x_n), on définit les coordonnées sphériques (r, ϕ₁, …, ϕ_n-1) par

$\begin{align} r &= ||x||\\ x_1 &= r\cos\phi_1\\ x_2 &= r\sin\phi_1 \cos \phi_2\\ \cdots\\ x_{n-1} &= r\sin\phi_1\,\cdots\,\sin\phi_{n-2}\cos\phi_{n-1}\\ x_n &= r\sin\phi_1\,\cdots\,\sin\phi_{n-2}\sin\phi_{n-1} \end{align}$

Les coordonnées sphériques constituent le cas particulier n = 3 et les polaires n = 2 ; on pourra consulter la section correspondante de l'article 3-sphère pour le cas n=4.

Sources

↑ ^{a, b et c} Eric W. Weisstein, « Spherical Coordinates." » sur From MathWorld
↑ International Organization for Standardization, ISO Standards Handbook : Quantities and units., 3rd ed., Genève, 1993, 345 p., ISBN 92-67-10185-4

Portail de la géométrie

Catégorie :

Système de coordonnées

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coordonnées sphériques de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Coordonnees spheriques — Coordonnées sphériques Un point repéré en coordonnées sphériques Les coordonnées sphériques sont un système de coordonnées de l espace qui généralise les coordonnées polaires du plan. Un point de l espace y est repéré par la distance à un pôle et … Wikipédia en Français
Coordonnées Sphériques — Un point repéré en coordonnées sphériques Les coordonnées sphériques sont un système de coordonnées de l espace qui généralise les coordonnées polaires du plan. Un point de l espace y est repéré par la distance à un pôle et deux angles, le… … Wikipédia en Français
coordonnées sphériques — sferinės koordinatės statusas T sritis automatika atitikmenys: angl. spherical coordinates vok. sphärische Koordinaten, f rus. сферические координаты, f pranc. coordonnées sphériques, f … Automatikos terminų žodynas
coordonnées sphériques — sferinės koordinatės statusas T sritis fizika atitikmenys: angl. spherical coordinates vok. sphärische Koordinaten, f rus. сферические координаты, f pranc. coordonnées sphériques, f … Fizikos terminų žodynas
Système de coordonnées sphériques — Coordonnées polaires Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une… … Wikipédia en Français
Coordonnees polaires — Coordonnées polaires Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une… … Wikipédia en Français
Coordonnées Polaires — Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une distance. Ce système est… … Wikipédia en Français
Coordonnées polaires (Mathématiques) — Coordonnées polaires Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une… … Wikipédia en Français
coordonnées — [ kɔɔrdɔne ] n. f. pl. • 1754; de co et ordonnée 1 ♦ Math. Coordonnées d un point M :scalaires qui permettent de repérer ce point sur une courbe, une surface, dans un espace. Coordonnées dans le plan euclidien (dans R2), dans l espace euclidien… … Encyclopédie Universelle
Coordonnées horizontales — ● Coordonnées horizontales coordonnées sphériques, pour un lieu donné, dans un système dont le plan fondamental est le plan horizontal, le pôle positif le zénith, et la direction origine l intersection du plan horizontal avec le plan méridien … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Coordonnées sphériques

Sommaire

Histoire