Multiplicateur de lagrange

Multiplicateur de Lagrange

Pour les articles homonymes, voir Théorème de Lagrange.

La méthode des multiplicateurs de Lagrange permet de trouver un optimum, sur la figure le point le plus élevé possible, tout en satisfaisant une contrainte, sur la figure un point de la ligne rouge.

Le multiplicateur de Lagrange est une méthode permettant de trouver les points stationnaires (maximum, minimum...) d'une fonction dérivable d'une ou plusieurs variables, sous contraintes.

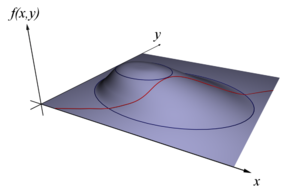
On cherche à trouver l'extremum, un minimum ou un maximum, d'une fonction φ de n variables à valeurs dans les nombres réels, ou encore d'un espace euclidien de dimension n, parmi les points respectant une contrainte, de type ψ(x) = 0 où ψ est une fonction du même ensemble de départ que φ. La fonction ψ est à valeurs dans un espace euclidien de dimension m. Elle peut encore être vue comme m fonctions à valeurs réelles, décrivant m contraintes. Si l'espace euclidien est de dimension 2 et si la fonction ψ est à valeurs dans R, correspondant à une contrainte mono-dimensionnelle, la situation s'illustre par une figure analogue à celle de droite. La question revient à rechercher le point situé le plus haut, c'est-à-dire le maximum de φ, dans l'ensemble des points rouges, c'est-à-dire ceux qui vérifient la contrainte.

Le théorème clé se conçoit aisément dans l'exemple de dimension 2. Le point recherché est celui où la courbe rouge ne monte ni ne descend. En termes plus techniques, cela correspond à un point où la différentielle de ψ possède un noyau orthogonal au gradient de φ en ce point. Le multiplicateur de Lagrange est une méthode offrant une condition nécessaire. Les fonctions φ et ψ sont différentiables et leurs différentielles continues, on parle de fonction de classe C¹. On considère λ un vecteur pris dans l'ensemble d'arrivée de ψ et la fonction L définie par :

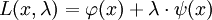
$L(x,\lambda) = \varphi(x) + \lambda\cdot \psi(x)$

L'opérateur représenté par un point est le produit scalaire. Si x₀ est une solution recherchée, il existe un vecteur λ₀ tel que la fonction L admet une différentielle nulle au point (x₀, λ₀). Les coordonnées du vecteur λ₀ sont appelées multiplicateurs de Lagrange. Cette technique permet de passer d'une question d'optimisation sous contrainte à une optimisation sans contrainte, celle de la fonction L.

La méthode se généralise aux espaces fonctionnels. Un exemple est donnée par la question de la chaînette, qui revient à rechercher la position que prend au repos, une chaînette attachée à ses deux extrémités. L'optimisation correspond à la position offrant un potentiel minimal, la contrainte est donnée par la position des extrémités et la longueur de la chaînette, supposée fixe. Cette méthode permet de trouver des plus courts chemins sous contrainte, ou encore des géodésiques. Le principe de Fermat ou celui de moindre action permet de résoudre de nombreuses questions à l'aide de cette méthode.

Hugh Everett généralise la méthode aux fonctions non-dérivables, souvent choisies convexes. Pour une résolution effective, il devient nécessaire de disposer d'un algorithme déterminant l'optimum (ou les optima) d'une fonction. Dans le cas non dérivable, on utilise souvent une heuristique adéquate.

Dimension finie

Exemple introductif

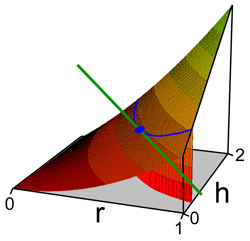La nappe correspond à la surface du cylindre, la courbe bleue aux points de volume égal à v₀, choisi dans la représentation égal à 1.

Soit v₀ un nombre strictement positif, l'objectif est de trouver la portion de cylindre de rayon r et de hauteur h de surface minimale et de volume v₀. Pour cela on définit deux fonctions, v et s qui à (r, h) associent respectivement le volume et la surface de la portion de cylindre. On dispose des égalités :

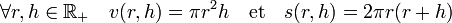
$\forall r,h \in \mathbb R_+\quad v(r,h) =\pi r^2h \quad\text{et}\quad s(r,h) =2\pi r(r+h)\;$

La figure de droite représente la fonction s, qui à r et h associe la surface. La ligne bleue correspond aux points de volume égal à 1, l'objectif est de trouver le point bleu, de plus petite surface pour un volume égal à 1.

On définit une fonction c et L de la manière suivante :

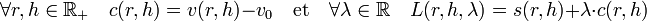
$\forall r,h \in \mathbb R_+\quad c(r,h) = v(r,h) - v_0\quad \text{et}\quad \forall \lambda \in \mathbb R \quad L(r,h,\lambda) = s(r,h) + \lambda \cdot c(r,h)$

La méthode de Lagrange consiste à rechercher un point tel que la différentielle de L soit nulle. Sur un tel point, la dérivée partielle en λ est nulle, ce qui signifie que la fonction c est nulle, ou encore que la contrainte est respectée. Si l'on identifie s avec son approximation linéaire tangente, son comportement sur la contrainte, aussi identifiée à son approximation linéaire tangente est aussi nécessairement nulle. Ce comportement est illustré par la droite en vert sur la figure. Le long de cette droite, la fonction c est nulle, à l'ordre 1, la fonction s l'est alors nécessairement.

Il suffit, en conséquence, de calculer la différentielle de L, et plus précisément ses trois dérivées partielles, pour l'exemple choisi :

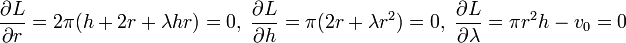
$\frac {\partial L}{\partial r} = 2\pi (h+ 2r + \lambda hr)=0 ,\; \frac {\partial L}{\partial h} = \pi(2r + \lambda r^2) =0,\; \frac {\partial L}{\partial \lambda} = \pi r^2 h - v_0=0$

On trouve les valeurs suivantes :

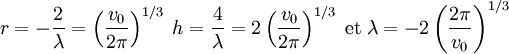
$r = -\frac 2{\lambda} = \left(\frac {v_0}{2\pi}\right)^{1/3}\; h = \frac 4{\lambda}=2\left(\frac {v_0}{2\pi}\right)^{1/3}\;\text{et}\; \lambda = -2\left(\frac {2\pi}{v_0}\right)^{1/3}$

Deuxième exemple : l'isopérimétrie du triangle

L'exemple précédent possède l'avantage d'une représentation graphique simple, guidant l'intuition. En revanche, il est trop simple pour que la méthode du multiplicateur de Lagrange soit la meilleure dans ce cas. En effet, on peut aussi calculer la valeur de h pour que l'aire de la frontière soit égale à v₀, on trouve :

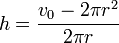
$h = \frac {v_0 - 2\pi r^2}{2\pi r}$

Il devient possible d'exprimer le volume du cylindre d'aire égale à v₀ en fonction de r et le calcul revient à trouver le minimum d'une fonction de R dans R.

Pour se convaincre de la pertinence de la méthode, on peut rechercher le triangle d'aire maximale et de périmètre p, choisi strictement positif. Si (x, y, z) est le triplet des longueurs des cotés du triangle, son aire A est égale à :

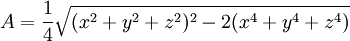
$A = \frac 14 \sqrt {(x^2 + y^2 + z^2)^2 - 2(x^4 + y^4 + z^4)}$

Il est plus simple de maximiser la fonction φ qui associe le quart du carré de A, la contrainte est donnée par la fonction ψ qui associe au triangle la différence du périmètre et de p :

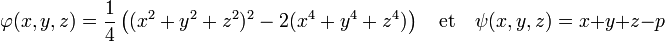
$\varphi (x,y,z) = \frac 14 \left((x^2 + y^2 + z^2)^2 - 2(x^4 + y^4 + z^4)\right) \quad\text{et}\quad \psi (x,y,z) = x+y+z - p$

Un triangle n'est défini, pour un couple (x, y, z), que si les trois coordonnées sont positives et si la somme de deux coordonnées est supérieure à la troisième. Soit D cet ensemble de points, sur la frontière de D, la fonction φ est nulle. On cherche un point de l'intérieur de D tel que φ soit maximal dans l'ensemble des points d'image par ψ nulle. Comme l'intersection de l'image réciproque de 0 par ψ et de D est un compact, il existe au moins un maximum. On définit comme dans l'exemple précédent la fonction L par :

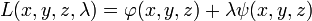
$L(x,y,z,\lambda) = \varphi(x,y,z) + \lambda\psi(x,y,z)\;$

Si (a, b, c) est un triangle de périmètre p et d'aire maximale, il existe une valeur λ₀ telle que la différentielle de L au point (a, b, c, λ₀) soit nulle. Un calcul de dérivée partielle montre que ce quadruplet est solution du système d'équations :

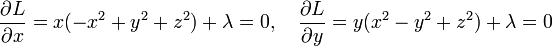
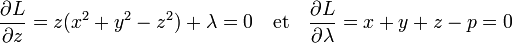
$\frac {\partial L}{\partial x} =x(-x^2 + y^2 + z^2) + \lambda = 0,\quad \frac {\partial L}{\partial y} =y(x^2 - y^2 + z^2) + \lambda = 0$ $\frac {\partial L}{\partial z} =z(x^2 + y^2 - z^2) + \lambda = 0\quad\text{et}\quad \frac {\partial L}{\partial \lambda} = x+y+z -p = 0$

On en déduit que a, b et c sont tous racines de l'équation :

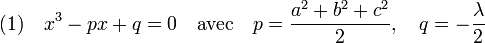
$(1)\quad x^3 - px + q = 0 \quad\text{avec}\quad p = \frac {a^2 + b^2 + c^2}2,\quad q = -\frac {\lambda}2$

Si les trois valeurs sont distinctes, elles correspondent aux trois racines de l'équation (1), leur somme est égale au coefficient de degré 2, c'est-à-dire à 0. Un tel point ne peut être dans l'intérieur de D car il est soit égal au triplet nul, soit contient une coordonnée strictement négative. On en conclut qu'au moins deux coordonnées sont égales, par exemple b et c. On peut alors ajouter une cinquième équation aux quatre que fournissent le calcul des dérivées partielles : y = z. En remplaçant z par y dans la première et deuxième équation, on obtient :

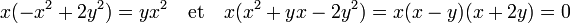
$x(-x^2 + 2y^2) = yx^2\quad\text{et}\quad x(x^2 + yx -2y^2) = x(x-y)(x+2y)=0$

On trouve trois cas : x = 0 correspond à un point de la frontière de D et c'est un minimum de φ, x = y correspond au triangle équilatéral et x = -2.y est un cas impossible car a est nécessairement strictement positif. L'unique solution est le triangle équilatéral de coté p/3 car a = b = c et la somme des trois longueurs est égale à p.

Remarque : L'objectif est ici d'illustrer la méthode du multiplicateur de Lagrange, on a trouvé le maximum d'une fonction φ dans l'intérieur de D, sous la contrainte définie par ψ. Si l'objectif est uniquement de résoudre le problème isopérimétrique pour le triangle, une solution plus simple est donnée dans l'article sur l'isopérimétrie.

Notations et interprétation géométrique

Soit E et F deux espaces vectoriels réels de dimensions respectives n et m avec n plus grand que m. Soit φ une fonction de E dans R, que l'on cherche à optimiser. On cherche un point a tel que φ(a) soit le plus petit possible. Soit ψ une fonction de E dans F, définissant la contrainte. L'ensemble sur lequel on travaille est G, correspondant aux points x tel que ψ(x) = 0.

Si (e₁, ..., e_n) est une base de E, chaque point x de E s'exprime comme une combinaison linéaire des éléments de la base :

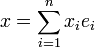
$x = \sum_{i=1}^n x_i e_i\;$

Cette remarque permet de voir les fonctions φ et ψ de deux manières. Elles peuvent être vues comme des fonctions d'une unique variable x de E, ce qui rend l'écriture plus concise et favorise une compréhension plus simple, mais plus abstraite des mécanismes en jeu. Les applications peuvent aussi être vues comme fonctions de n variables x₁, ..., x_n, ce qui présente une rédaction plus lourde mais plus aisée pour les calculs effectifs. L'espace F est de dimension m, si (f₁, ..., f_m) est une base de F, la fonction ψ peut aussi être vue comme m fonctions de n variables :

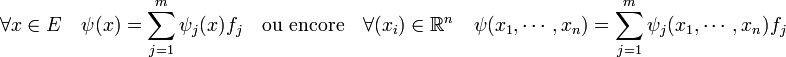
$\forall x \in E \quad \psi(x) = \sum_{j=1}^m \psi_j(x) f_j \quad\text{ou encore}\quad \forall (x_i) \in \mathbb R^n \quad \psi(x_1,\cdots, x_n) = \sum_{j=1}^m \psi_j(x_1,\cdots, x_n) f_j$

L'ensemble G peut être vu comme une unique contrainte exprimée par une fonction à valeurs dans F ou encore comme m contraintes exprimées par les égalités ψ_j(x) = 0, à valeurs dans R.

Un corollaire du théorème de Rolle indique que l'optimum est atteint en un point de différentielle nulle.

Le fondement théorique de la méthode du multiplicateur de Lagrange peut être vu comme analogue au théorème de Rolle.

Les fonctions φ et ψ sont de classe C¹, ce qui signifie qu'elles sont différentiables, autrement dit elles admettent chacune une application linéaire tangente en chaque point. Le terme C¹ signifie aussi que les applications qui, à un point associent les différentielles, soit de φ soit de ψ sont continues.

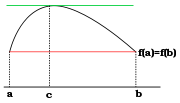
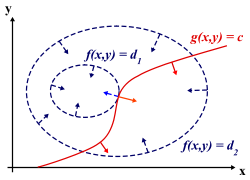
L'optimum recherchée vérifie une propriété analogue à celle du théorème de Rolle. un corollaire de ce théorème, illustré à gauche, indique que l'optimum, un maximum ou un minimum,s'il se situe dans l'intervalle ouvert ]a, b[, possède une tangente horizontale, ce qui signifie encore que sa différentielle est nulle. C'est un résultat de cette nature qui est recherché. On peut le visualiser sur la figure de droite, si n et m sont respectivement égaux à 2 et à 1. On représente φ (noté f sur la figure de droite) en bleu par ses courbes de niveau, comme les géographes. Les flèches représentent le gradient de la fonction φ. La différentielle de φ est une application linéaire de E dans R, c'est-à-dire une forme duale. Il est d'usage de considérer E comme un espace euclidien, de choisir la base de E orthonormale et d'identifier la différentielle avec le vecteur de E qui représente la forme duale. Dans ce cas, l'approximation linéaire tangente s'écrit :

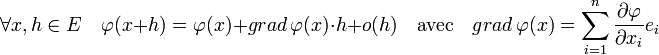
$\forall x,h \in E \quad \varphi(x+h) = \varphi(x) + grad \,\varphi (x)\cdot h + o(h)\quad\text{avec}\quad grad \,\varphi(x) = \sum_{i=1}^n \frac {\partial \varphi}{\partial x_i}e_i$

La lettre o désigne un petit o selon la notation de Landau et le point entre le gradient de φ et h symbolise le produit scalaire. Le vecteur gradient est orthogonal à la courbe de niveau, dans le sens des valeurs croissantes de φ et de norme proportionnelle à la vitesse d'accroissement de φ dans cette direction. La contrainte vérifie une propriété analogue puisqu'elle est aussi différentiable. L'ensemble étudié est celui des valeurs x tel que ψ(x) est nul. Si x₀ est élément de G, les points voisins de x₀ dans G ont aussi une image nulle par ψ, autrement dit, l'espace tangent à G au point x₀ est formé par les accroissements h de x₀ qui ont une image par la différentielle de ψ nulle. La direction de l'espace tangent est le noyau de l'application différentielle de ψ. Une analyse par les fonctions coordonnées ψ_i exprime ce résultat en indiquant que l'espace tangent est l'intersection des hyperplans orthogonaux des gradients de ψ_i.

Une analyse au point optimal x₀ recherché indique, en approximation du premier ordre, qu'un déplacement h dans la direction de l'espace tangent à G ne peut pas accroître la valeur de φ. Ceci signifie que le déplacement h est nécessairement orthogonal au gradient de φ en x₀. C'est ainsi que se traduit le théorème de Rolle, dans ce contexte. Géométriquement, cela signifie que la courbe de niveau bleue et la ligne rouge sont tangentes au point recherché. Analytiquement cela se traduit par le fait que le noyau de la différentielle de ψ en x₀ est orthogonal au gradient de φ en ce point.

Théorèmes

Le problème à résoudre est de trouver le minimum suivant :

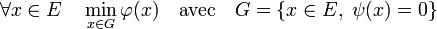
$\forall x \in E \quad \min_{x \in G} \varphi (x) \quad\text{avec}\quad G = \{x \in E,\; \psi(x)=0\}$

Les fonctions φ et ψ ne sont pas nécessairement définies sur tout E mais au moins sur des ouverts de E. De plus, le domaine de définition de φ possède une intersection non vide avec G.

La méthode des multiplicateurs de Lagrange se fonde sur un théorème.

Théorème du multiplicateur de Lagrange — Si le point x₀ est un extremum local de φ dans l'ensemble G, alors le noyau de la différentielle de ψ au point x₀ est orthogonal au gradient de φ en ce point.^[1]

Un corollaire met en évidence le multiplicateur. Pour cela, il est nécessaire d'équiper F du produit scalaire tel que sa base soit orthonormale, le symbole ^t signifie la transposée d'une l'application linéaire, elle définit une application du dual de F, ici identifié à F dans le dual de E, encore identifié à E :

Corollaire 1 — Si le point x₀ est un extremum local de φ dans l'ensemble G et si la différentielle de ψ au point x₀ est surjective, il existe un vecteur λ₀ de F tel que la somme de l'image de λ₀ par la transposée de la différentielle de ψ au point x₀ et du gradient de φ en ce point soit nulle :

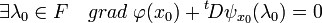
$\exists \lambda_0 \in F \quad grad\; \varphi (x_0) + {}^t\!D\psi_{x_0} (\lambda_0) = 0$

Sous forme de coordonnées, on obtient :

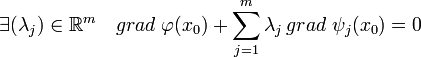
$\exists (\lambda_j) \in \mathbb R^m \quad grad\; \varphi (x_0) + \sum_{j=1}^m \lambda_j \, grad \; \psi_j (x_0) = 0$

Un deuxième corollaire est plus pragmatique, car il offre une méthode effective pour déterminer l'extremum. Il correspond à la méthode utilisée dans l'exemple introductif.

Corollaire 2 — Si le point x₀ est un extremum local de φ dans l'ensemble G et si la différentielle de ψ au point x₀ est surjective, alors il existe un vecteur λ₀ de F tel que la fonction L de ExF dans R admet un gradient nul en (x₀, λ₀) :^[2]

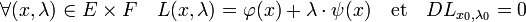
$\forall (x,\lambda) \in E\times F \quad L(x,\lambda) = \varphi(x) + \lambda \cdot \psi (x)\quad \text{et}\quad DL_{x_0,\lambda_0} = 0$

Ces théorèmes possèdent quelques faiblesses, de même nature que celle du théorème de Rolle. La condition est nécessaire, mais pas suffisante. Un point de dérivée nulle pour Rolle ou vérifiant les hypothèses du théorème du multiplicateur de Lagrange n'est pas nécessairement un maximum ou un minimum. Ensuite, même si ce point est un extremum, il n'est que local. Si une solution x₀ est trouvée, rien n'indique que cet extremum local est le meilleur. L'approximation linéaire ne précise pas si cet optimum est un maximum ou un minimum. Enfin, comme pour le cas du théorème de Rolle, si les domaines de définition ne sont pas ouverts, il est possible qu'un point frontière soit un optimum qui ne vérifie pas le théorème. Ainsi, sur la figure de gauche, f(a) et f(b) sont des minima, mais la dérivée n'est nulle ni en a ni en b.

Démonstrations

Il existe deux méthodes célèbres pour démontrer les résultats de Lagrange. La première est souvent appelée méthode des pénalités^[3], elle consiste à considérer une suite (χ _k) définie de la manière suivante :

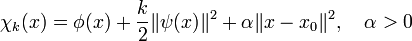
$\chi_k (x) = \phi (x) + \frac k2 \|\psi(x)\|^2 + \alpha \|x - x_0\|^2,\quad \alpha > 0$

La suite des minima de ces fonctions tend vers x₀. L'autre méthode^[4] utilise le théorème des fonctions implicites. C'est un dérivé de cette méthode qui est utilisé ici. Le théorème n'est pas utilisé, mais les inégalités à la base de la démonstration sont présentes dans la preuve.

Cas où ψ est une fonction affine :

La démonstration de ce cas particulier n'est pas nécessaire pour le cas général, en revanche, elle permet de comprendre la logique utilisée et fixe les notations. Soit x₁ un point de E tel que la différentielle de ψ possède un noyau qui n'est pas dans l'orthogonal du gradient de φ. On montre que x₁ n'est pas un extremum. La contraposée de ce résultat permet de conclure.

Par hypothèse il existe un vecteur k₁ élément de la différentielle de ψ au point x₁ (qui est d'ailleurs la même en chaque point car ψ est une application affine) et qui n'est pas orthogonal au gradient. On choisit k₁ de norme 1 et de sens tel que le produit scalaire de ce vecteur avec le gradient soit strictement positif. On note α ce produit scalaire. Si s est un réel positif, l'égalité définissant le gradient, appliquée au vecteur s.k₁ est :

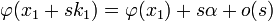
$\varphi(x_1 + sk_1) = \varphi(x_1) + s\alpha + o(s)\;$

si s est choisi suffisamment petit, alors o(s) peut être choisi plus petit, en valeur absolue, que n'importe quelle constante strictement positive que multiplie s, par exemple : s.α/2. De manière formelle :

$\exists \mu>0,\; \forall s \in ]0, \mu[ \quad \varphi (x_1 + sk_1) \ge \varphi(x_1) + s\alpha - \frac {s\alpha}2 = \varphi(x_1) + \frac {s\alpha}2$

Le fait que l'image par ψ de x₁ + s.k₁ soit un élément de G ainsi que la majoration précédente, montrent que x₁ ne peut être un maximum local. En choisissant s négatif, on montre que x₁ ne peut pas non plus être un minimum local.

Cas général :

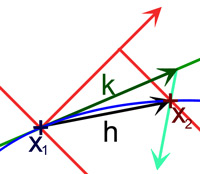
Dans le cas général, on ne peut supposer que x₁ + s.k₁ soit élément de G. La situation est illustrée sur la figure de droite. L'ensemble G est représenté en bleu, le gradient de φ en rouge et la droite dirigée par k₁ en vert. Pour une valeur de s suffisamment petite, on construit un vecteur k, égal à s.k₁ et proche de G. Une technique analogue à celle du théorème des fonctions implicites permet de trouver un point x₂, suffisamment proche de x₁ + k pour que le raisonnement précédent puisse s'appliquer avec peu de modifications. La technique consiste à établir quatre inégalités qui montrent le résultat recherchée.

Première inégalité :

Elle consiste à utiliser la définition du gradient au point x₁, mais cette fois ci, valable pour tout vecteur de norme suffisamment petite :

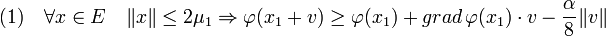
$(1)\quad \forall x \in E \quad \|x\| \le 2\mu_1 \Rightarrow \varphi(x_1 + v) \ge \varphi (x_1) + grad \,\varphi(x_1)\cdot v - \frac {\alpha}8\|v\|$

Par rapport au cas particulier affine, la constante est choisie un peu différemment, elle est maintenant égale à α/8. La zone sur laquelle la majoration est vérifiée est un peu modifiée, elle correspond maintenant aux vecteurs de normes plus petites que 2μ₁. Les raisons techniques qui poussent à ces modifications apparaissent à la conclusion de cette démonstration.

Deuxième inégalité :

La deuxième inégalité permet de borner la norme du vecteur, illustré en bleu ciel et qu'il faut ajouter à x₁ + s.k₁ pour retrouver le point de G qui montre que x₁ n'est pas un maximum local. L'objectif est de montrer qu'il existe un réel strictement positif m tel que :

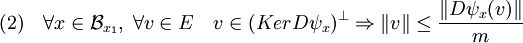
$(2)\quad \forall x \in \mathcal B_{x_1},\; \forall v \in E \quad v \in (Ker D\psi_x)^{\bot} \Rightarrow \|v\| \le \frac {\|D\psi_x(v)\|}m$

Ici le symbole B_x₁ désigne la boule de centre x₁ et de rayon 1. Pour établir ce résultat, on utilise deux propriétés des compacts. Une fonction continue l'est uniformément sur un compact, ensuite elle atteint sa borne inférieure. La différentielle de ψ en un point quelconque est continue, comme d'ailleurs toute application linéaire en dimension finie. Composée avec la norme, aussi continue, elle atteint sa borne inférieure sur l'intersection de l'orthogonal de son noyau et de la sphère unité. Cette intersection est en effet compact. On appelle f la fonction qui à une application linéaire de E dans F associe cette borne inférieure. Par construction elle ne peut prendre de valeur nulle. On considère ensuite la fonction g, qui à x élément de E associe l'image par f de la différentielle de ψ au point x. Une fois sa continuité sur la boule fermée de centre x₁ et de rayon 1 démontrée, on sait que cette fonction atteint son minimum m. La majoration (2) définit ce minimum.

Pour établir l'inégalité (2) il suffit donc démontrer la continuité de g. L'application qui à x associe la différentielle de ψ au point x est continue par hypothèse. Elle est donc uniformément continue sur la boule de centre x₁ et de rayon 1 :

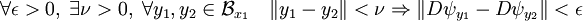
$\forall \epsilon >0,\; \exists \nu >0 ,\;\forall y_1, y_2 \in \mathcal B_{x_1} \quad \|y_1 - y_2\| < \nu \Rightarrow \|D\psi_{y_1} - D\psi_{y_2}\|<\epsilon$

Soit v₁ (resp. v₂) un vecteur de norme 1, tel que :

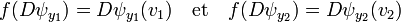
$f(D\psi_{y_1}) = D\psi_{y_1}(v_1) \quad\text{et}\quad f(D\psi_{y_2}) = D\psi_{y_2}(v_2)$

L'espace des applications linéaires de E dans F est muni de la norme qui associe à une application la borne supérieure des normes de son image de la boule unité. Comme les points y₁ et y₂ sont choisis à une distance inférieure à

ν

l'un de l'autre. On dispose de la majoration :

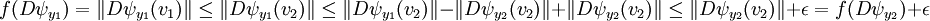
$f(D\psi_{y_1}) = \|D\psi_{y_1}(v_1)\| \le \|D\psi_{y_1}(v_2)\| \le \|D\psi_{y_1}(v_2)\| - \|D\psi_{y_2}(v_2)\| + \|D\psi_{y_2}(v_2)\| \le \|D\psi_{y_2}(v_2)\| + \epsilon = f(D\psi_{y_2}) + \epsilon$

Cette majoration, ainsi que la même appliquée à y₂, démontre la continuité recherchée pour conclure la preuve de la majoration (2) :

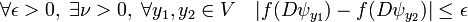
$\forall \epsilon >0,\; \exists \nu >0 ,\; \forall y_1, y_2 \in V \quad |f(D\psi_{y_1}) - f(D\psi_{y_2})| \le \epsilon$

Troisième inégalité :

On dispose d'une majoration comparable à (1), mais cette fois appliquée à ψ et utilisant la continuité uniforme. Il existe un réel strictement positif μ₂ tel que, si θ désigne l'angle entre le gradient de φ au point x₁ et k :

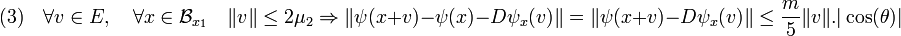
$(3)\quad \forall v \in E,\quad \forall x \in \mathcal B_{x_1} \quad \|v\| \le 2\mu_{2} \Rightarrow \|\psi(x + v) - \psi(x) - D\psi_{x}(v)\| = \|\psi(x + v) - D\psi_{x}(v)\| \le \frac m5 \|v\|.|\cos (\theta)|$

Quatrième inégalité :

La fonction Dψ, qui au point x associe la différentielle de ψ au point x est continue, en particulier au point x₁, ce qui montre que :

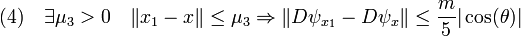
$(4)\quad \exists \mu_3 >0 \quad \|x_1 - x \|\le \mu_3 \Rightarrow \|D\psi_{x_1} - D\psi_x\|\le \frac m5|\cos (\theta)|$

Une fois les quatre inégalités établies, il devient possible de définir les vecteurs h et k et de conclure. Soient s un réel strictement strictement positif et plus petit que μ₁, μ₂, μ₃ et que 1/2, on définit le vecteur k de la figure comme étant égal à s.k₁. Soit x₂ le vecteur le plus proche de x + k et élément de G et h le vecteur x₂ - x₁. Enfin l₁ désigne le vecteur colinéaire à h - k de même sens et de norme 1, c'est le vecteur illustré en bleu ciel de la figure. Le réel positif t est tel que t.l₁ soit égal à h - k. Le choix du vecteur k est tel que t est suffisamment petit pour conclure.

Conclusion :

Le point t.l₁ est le plus petit vecteur de E tel que x₁ + s.k₁ + t.l₁ est un élément de G. Autrement dit :

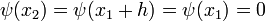
$\psi(x_2) = \psi(x_1+h) = \psi(x_1) = 0\;$

La majoration (3), appliquée au point x₂, se traduit par :

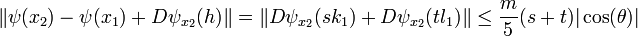
$\|\psi(x_2) - \psi(x_1) + D\psi_{x_2}(h)\| = \|D\psi_{x_2}(sk_1) + D\psi_{x_2}(tl_1)\|\le \frac{m}5(s+t)|\cos (\theta)|$

De plus, par définition de k₁ la différentielle de ψ est nulle sur k₁ en x₁, on en déduit d'après la majoration (4) :

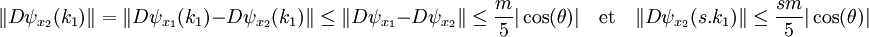
$\| D\psi_{x_2}(k_1)\| = \| D\psi_{x_1}(k_1) - D\psi_{x_2}(k_1)\|\le \| D\psi_{x_1} - D\psi_{x_2}\| \le \frac m5|\cos (\theta)|\quad\text{et}\quad \| D\psi_{x_2}(s.k_1)\| \le \frac{sm}5 |\cos (\theta)|$

Le point t.l₁ est le plus petit vecteur de E tel que x₁ + s.k₁ + t.l₁ est un élément de G. On remarque que x₁ est un élément de G. En conséquence, x₁ + s.k₁ - s.k₁ est aussi un élément de G et t.l₁ est de norme plus petite que s.k₁, ce qui revient à dire que t est plus petit que s, donc :

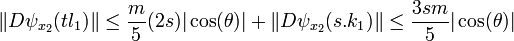
$\| D\psi_{x_2}(tl_1)\|\le \frac{m}5(2s)|\cos (\theta)| + \| D\psi_{x_2}(s.k_1)\| \le \frac{3sm}5 |\cos (\theta)|$

Le vecteur l₁ est orthogonal au noyau de Dψ au point x₂. En effet, le point x₂ est le plus proche de x₂ - t.l₁ dans G. Si p est un vecteur du noyau, x₂ + u.p est plus loin de x₂ - t.l₁ que ne l'est x₂, ici u désigne un nombre réel :

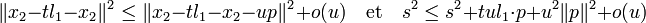
$\|x_2 - tl_1 - x_2\|^2 \le \|x_2 - tl_1 - x_2 - up\|^2 + o(u) \quad\text{et}\quad s^2 \le s^2 + tu l_1\cdot p + u^2\|p\|^2 + o(u)$

Ce qui montre que :

$\exists \epsilon >0,\; \forall u \in ]-\epsilon,\epsilon[ \quad u(t l_1\cdot p + u\|p\|^2) \ge 0$

Le produit scalaire de l₁ et p est nul, ce qui montre bien que l₁ est orthogonal au noyau de Dψ au point x₂. Le point x₂ est élément de la boule de rayon 1 et centre x₁. La majoration (2) montre que :

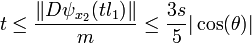
$t\le \frac {\|D\psi_{x_2}(tl_1)\|}m \le \frac {3s}5|\cos (\theta)|$

On peut maintenant appliquer la majoration (1) :

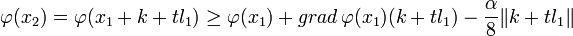
$\varphi(x_2) = \varphi(x_1+k+ tl_1) \ge \varphi(x_1) + grad\,\varphi(x_1)(k + tl_1) - \frac {\alpha}8 \|k + tl_1\|$

$\|grad\,\varphi(x_1)\||\cos (\theta)| = \alpha \quad\text{donc}\quad \varphi(x_2) \ge \varphi(x_1) + s\alpha - \frac 35 s\alpha - \frac 15 s\alpha = \varphi(x_1) + \frac 1{5} s\alpha$

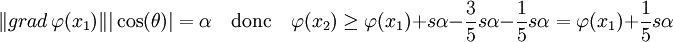
Le point x₂ est un élément de G ayant une image par φ strictement plus grande que x₁, ce qui montre que x₁ n'est pas un maximum local. On montre de même que x₁ n'est pas non plus un minimum local, ce qui termine la démonstration.

Il existe un vecteur λ₀ de F tel que la somme de l'image de λ₀ par la transposée de la différentielle de ψ au point x₀ et du gradient de φ en ce point soit nulle :

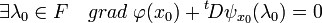
$\exists \lambda_0 \in F \quad grad\; \varphi (x_0) + {}^t\!D\psi_{x_0} (\lambda_0)=0$

C'est une conséquence directe du résultat précédent et des propriétés de la transposition. Remarquons tout d'abord que l'image de la transposée d'une application linéaire est un sous-espace vectoriel inclus dans l'orthogonal du noyau. Pour s'en convaincre, montrons qu'un élément v de l'image de la transposée de la différentielle de ψ au point x₀, d' antécédent de λ, possède un produit scalaire avec un élément w du noyau de la différentielle, nul :

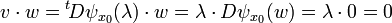
$v\cdot w = {}^t\!D\psi_{x_0}(\lambda)\cdot w = \lambda\cdot D\psi_{x_0}(w) = \lambda \cdot 0 = 0$

Montrons maintenant que l'orthogonal du noyau de la différentielle possède la même dimension que l'image de la transposée. L'application différentielle est surjective, son image est de dimension m, la transposée ne modifie pas le rang d'une application linéaire, l'image de sa transposée est donc aussi de dimension m. La somme des dimensions de l'image et du noyau est égale à celle de l'espace vectoriel de départ, ici E de dimension n. Comme l'image est de dimension m, le noyau est de dimension n - m. L'orthogonal du noyau est donc de dimension m. Pour résumer, l'orthogonal du noyau de la différentielle contient l'image de sa transposée et est de même dimension, ce qui montre l'égalité des deux sous-espaces vectoriels. Le gradient de φ au point x₀ est dans l'orthogonal au noyau de la différentielle, il est donc dans l'image de sa transposée, ce qui montre l'existence du vecteur λ₀.

Il existe un vecteur λ₀ de F tel que la fonction L de ExF dans R admet un gradient nul en (x₀, λ₀) :

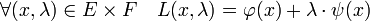
$\forall (x,\lambda) \in E\times F \quad L(x,\lambda) = \varphi(x) + \lambda \cdot \psi (x)$

Pour cela calculons l'image de (u, μ), un point de ExF par la différentielle de L au point (x₀, λ₀), λ₀ étant le vecteur de F défini lors de la démonstration précédente

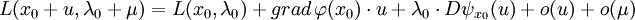
$L(x_0 + u, \lambda_0 + \mu) = L(x_0, \lambda_0) + grad\, \varphi(x_0)\cdot u + \lambda_0\cdot D\psi_{x_0}(u) +o(u) + o(\mu)$

La définition de λ₀ montre que :

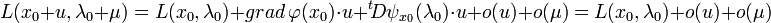
$L(x_0 + u, \lambda_0 + \mu) = L(x_0, \lambda_0) + grad\, \varphi(x_0)\cdot u + {}^t\!D\psi_{x_0}(\lambda_0)\cdot u +o(u) + o(\mu) = L(x_0, \lambda_0) +o(u) + o(\mu)$

Le gradient recherché est bien nul au point étudié.

Écriture du problème

Si l'écriture condensée permet de mieux comprendre la structure du théorème, les notations développées sont plus utiles pour une résolution effective. Dans la pratique, on considère souvent une fonction φ de Rⁿ dans R et m fonctions ψ_j, avec j variant de 1 à m, aussi de Rⁿ dans R. L'entier m est nécessairement plus petit que n pour pouvoir appliquer les théorèmes du paragraphe précédent. On cherche à trouver un n-uplet (a₁, ..., a_n) tel que :

$(1)\quad \varphi (a_1,\cdots , a_n) = \min_{(x_i) \in G} \varphi(x_1,\cdots,x_n)\quad\text{avec}\quad G = \{(x_i)\in \mathbb R^n, \quad \forall j \in [1,m] \;\psi_j (x_1,\cdots, x_n)=0\}$

Pour cela, on définit la fonction L de R^n+m dans R par :

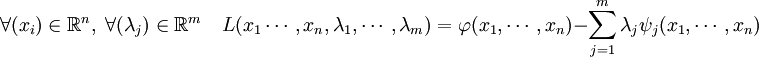
$\forall (x_i) \in \mathbb R^n,\; \forall (\lambda_j) \in \mathbb R^m \quad L(x_1\cdots, x_n,\lambda_1,\cdots, \lambda_m) =\varphi(x_1,\cdots,x_n) - \sum_{j=1}^m \lambda_j \psi_j(x_1,\cdots, x_n)$

Le deuxième corollaire indique que résoudre les équations suivantes offrent sur condition nécessaire pour élucider le problème d'optimisation (1). Le n-uplet (a₁, ..., a_n) est une solution de (1) seulement s'il existe un m-uplet (α₁,...,α_m) tel que le n+m-uplet (a₁, ..., a_n, α₁,...,α_m) soit solution des n + m équations :

$\forall i \in [1,n]\quad \frac {\partial \varphi}{\partial x_i}(x_1,\cdots, x_n) + \sum_{j=1}^m \lambda_j \frac {\partial \psi_j}{\partial x_i}(x_1,\cdots, x_n) = 0 \quad \text{et}\quad \forall j \in [1,m]\quad \psi_j(x_1,\cdots, x_n) = 0$

Cette méthode peut être généralisée aux problèmes d'optimisation incluant des contraintes d'inégalités (ou non linéaires) en utilisant les conditions de Kuhn-Tucker. Mais également sur des fonctions discrètes à maximiser ou minimiser sous contraintes, moyennant un changement d'interprétation, en utilisant la méthode des multiplicateurs d'Everett (ou de Lagrange généralisés), plus volontiers appelée méthode des pénalités.

Application : inégalité arithmético-géométrique

Article détaillé : Inégalité arithmético-géométrique.

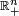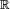La méthode du multiplicateur de Lagrange permet de démontrer l'inégalité arithmético-géométrique^[5]. On définit les applications φ et ψ de $\scriptstyle{ \R_+^n}$ dans $\scriptstyle \R$ par :

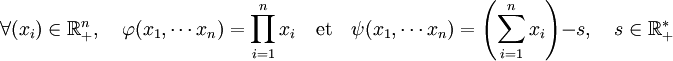
$\forall (x_i) \in \mathbb R_+^{n},\quad \varphi (x_1,\cdots x_n) = \prod_{i=1}^n x_i\quad\text{et}\quad \psi(x_1,\cdots x_n) = \left(\sum_{i=1}^n x_i\right) - s,\quad s\in \mathbb R_+^{*}$

On remarque que l'ensemble G, composé des n-uplets de coordonnées positives et de somme égale à $\scriptstyle s$ est un compact de 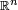$\scriptstyle{ \R^n}$ . Sur ce compact la fonction φ est continue, elle admet nécessairement un maximum. Les deux fonctions φ et ψ sont bien de classe 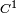$\scriptstyle{ C^1}$ , il est donc possible d'utiliser le multiplicateur de Lagrange pour trouver ce maximum. Pour cela, on considère la fonction L :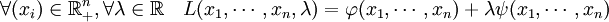

$\forall (x_i) \in \mathbb R_+^{n}, \forall \lambda \in \mathbb R \quad L(x_1,\cdots, x_n,\lambda) = \varphi(x_1,\cdots, x_n) + \lambda\psi(x_1,\cdots, x_n)$

Une solution vérifie les équations :

$\forall i \in [1,n] \quad \frac {\partial L}{\partial x_i} L(x_1,\cdots x_n,\lambda) = 0 \Leftrightarrow \prod_{k \neq i} x_k = -\lambda\quad \text{et}\quad \sum_{i=1}^n x_i = s$

On en déduit l'existence d'une unique solution, obtenue pour tous les 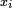$\scriptstyle{ x_i}$ égaux à 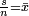$\scriptstyle{ \frac s n = \bar x}$ et λ égal à 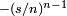$\scriptstyle{ -(s/n)^{n-1}}$ . Ce qui s'exprime, en remplaçant s par sa valeur :

$\forall (x_i) \in \mathbb R_+^{n} \quad \sqrt[n]{\prod_{i=1}^n x_i} \le \frac{\sum_{i=1}^n x_i}n$

La moyenne géométrique est inférieure à la moyenne arithmétique, l'égalité n'ayant lieu que si les 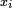$\scriptstyle{ x_i}$ sont tous égaux.

Le multiplicateur de Lagrange offre une démonstration alternative de l'inégalité arithmético-géométrique.

Espace fonctionnel

Exemple introductif : La chaînette

Article détaillé : Chaînette.

Le Viaduc de Garabit possède une arche dont la géométrie est celle d'une chaînette.

Il existe un autre contexte, qui fait appel au multiplicateur de Lagrange. Considérons une chaînette soumis à la gravité et recherchons son équilibre statique. La chaînette est de longueur a et l'on suppose qu'elle est accrochée à deux points d'abscisses -t₀ et t₀ et d'ordonnée nulle en ces deux points. Si son ordonnée est notée x, elle suit une courbe y=x(t) sur l'intervalle [-t₀, t₀], dont on se propose de calculer l'équation.

Dire qu'elle est à l'équilibre revient à dire que son potentiel Φ est minimal, où :

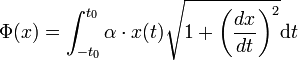
$\Phi(x) = \int_{-t_0}^{t_0}\alpha \cdot x(t)\sqrt{ 1 + \left(\frac {dx}{dt}\right)^2} \mathrm d t$

Ici, α désigne une constante physique, en l'occurrence le produit de g la gravitation terrestre, par la densité linéaire de la chaînette, supposée constante. La formule donnant la longueur d'un arc en fonction d'un paramétrage est donnée dans l'article Longueur d'un arc.

La chaînette n'est pas supposée être élastique, elle vérifie donc la contrainte Ψ, indiquant que sa longueur l₀ n'est pas modifiée :

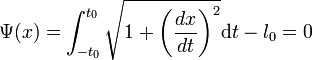
$\Psi(x) = \int_{-t_0}^{t_0}\sqrt{ 1 + \left(\frac {dx}{dt}\right)^2} \mathrm d t - l_0 = 0$

Si C¹_K(I) désigne l'ensemble des fonctions de [-t₀, t₀] dans R, dérivables et de dérivées continues, nulles en -t₀ et t₀, le problème revient à rechercher la fonction x₀ telle que :

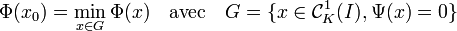
$\Phi (x_{0}) = \min_{x \in G} \Phi (x)\quad\text{avec}\quad G = \{x \in \mathcal C_K^1(I), \Psi(x) = 0\}$

La similitude avec la situation précédente est flagrante. Pour pouvoir appliquer des multiplicateurs de Lagrange, il faut donner un sens au gradient de Φ et Ψ. Dans le cas où il existe deux fonctions de classe C² de R³ dans R, notées φ et ψ telles que :

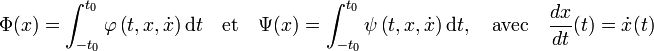
$\Phi(x) = \int_{-t_0}^{t_0} \varphi\left(t, x, \dot x\right) \mathrm d t \quad\text{et}\quad \Psi(x) = \int_{-t_0}^{t_0} \psi\left(t, x , \dot x\right) \mathrm d t,\quad\text{avec}\quad \frac {dx}{dt}(t) = \dot x(t)$

L'équation d'Euler-Lagrange affirme que :

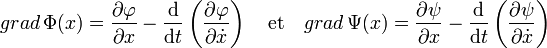
$grad\,\Phi(x) = \frac{\partial \varphi}{\partial x}-\frac{\mathrm d}{ \mathrm dt}\left( \frac{\partial \varphi}{\partial \dot x} \right)\quad\text{et}\quad grad\,\Psi(x) = \frac{\partial \psi}{\partial x}-\frac{\mathrm d}{ \mathrm dt}\left( \frac{\partial \psi}{\partial \dot x} \right)$

Dans le cas particulier où les fonctions φ et ψ sont des fonctions de deux variables et ne dépendent pas de t, on obtient la formulation de Beltrami (cf l'article Équation d'Euler-Lagrange):

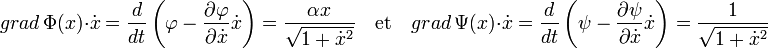
$grad\,\Phi(x) \cdot \dot x = \frac d{dt}\left(\varphi -\frac {\partial \varphi}{\partial \dot x}\dot x\right) = \frac {\alpha x}{\sqrt{1+ \dot x^2}}\quad\text{et}\quad grad\,\Psi(x) \cdot \dot x = \frac d{dt}\left(\psi -\frac {\partial \psi}{\partial \dot x}\dot x\right) = \frac 1{\sqrt{1+ \dot x^2}}$

Dire que les deux gradients sont colinéaires revient à dire qu'il existe un réel λ, le multiplicateur de Lagrange, tel que :

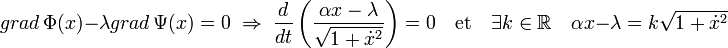
$grad\,\Phi(x) -\lambda grad\,\Psi(x) = 0 \;\Rightarrow\; \frac {d}{dt} \left(\frac {\alpha x - \lambda}{\sqrt{1+ \dot x^2}}\right) = 0\quad\text{et}\quad \exists k \in \mathbb R \quad \alpha x - \lambda = k\sqrt{1+ \dot x^2}$

La résolution de cette équation différentielle est une chaînette. La méthode du multiplicateur de Lagrange permet bien de résoudre la question posée^[6].

Espace de Sobolev

Article détaillé : Espace de Sobolev.

L'exemple précédent montre que le contexte de l'équation d'Euler-Lagrange n'est pas loin de celui du multiplicateur de Lagrange. Si l'ensemble de départ de la fonction x(t) recherchée est un intervalle I ouvert et borné de R et l'ensemble d'arrivée E l'espace vectoriel euclidien, la généralisation est relativement aisée.

On suppose l'existence d'une fonction Φ à minimiser, son ensemble de départ est un espace fonctionnel, c'est-à-dire un espace vectoriel de fonctions, de I dans E et son ensemble d'arrivée R. La fonction Φ est construite de la manière suivante :

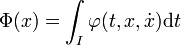
$\Phi(x) = \int_I \varphi(t,x,\dot x) \mathrm d t$

Le point sur le x indique la fonction gradient, qui à t associe le gradient de x au point t.

La fonction φ est une fonction de RxE² dans R de classe C². L'optimisation est sous contrainte, donnée sous une forme analogue à la précédente. On suppose l'existence d'une fonction Ψ de RxE² dans F, un espace euclidien. La fonction Ψ est encore définie à l'aide d'une fonction ψ de classe C² de IxE², mais cette fois dans F un espace euclidien:

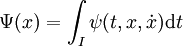
$\Psi(x) = \int_I \psi(t,x,\dot x) \mathrm d t$

L'ensemble G est composée de fonctions deux fois dérivables de I dans E et dont l'image par Ψ est nulle. On suppose de plus que les valeurs des fonctions de G aux bornes de I sont fixes et, quitte à opérer une translation, on peut toujours supposer, sans perte de généralités, que ces fonctions sont nulles aux bornes de I.

La seule tâche un peu délicate est de définir l'espace vectoriel W^2,2(I,E) sur lequel opère Φ et Ψ. Pour définir un équivalent de gradient, cet espace comporte nécessairement un produit scalaire. Si l'on souhaite établir des théorèmes équivalents aux précédents les fonctions dérivées et dérivées seconde sont définies et l'espace est complet. Un espace munis d'un produit scalaire et complet est un Hilbert. Sa géométrie est, de fait, suffisamment riche pour étendre les résultats précédents.

On note D l'espace des fonctions de I, à valeur dans E, de classe C et à support compact et D^* son dual topologique. L'espace D est munis de la norme de la borne supérieure et l'espace D^* est celui des distributions. Ce premier couple n'est pas encore satisfaisant car D est trop petit et D^* trop gros pour permettre de définir un bon produit scalaire, à l'origine d'une géométrie aussi simple que celle d'un Hilbert.

L'espace D^* contient le Hilbert des fonctions de carrés intégrables L²(I,E). En effet une fonction f de L²(I,E) agit sur D par le produit scalaire <.,.>_L défini par l'intégrale de Lebesgue :

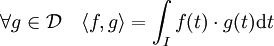
$\forall g \in \mathcal D \quad \langle f,g\rangle = \int_I f(t)\cdot g(t) \mathrm d t$

C'est dans L²(I,E) que nous cherchons le bon espace. Dans cet espace, l'intégration par parties permet de définir la dérivée de la fonction f de L²(I). Comme g est à support compact et que I est ouvert, aux bornes de I, la fonction g est nulle. Si f est dérivable au sens classique du terme, on bénéficie des égalités :

$\langle \dot f,g\rangle_L = \int_I \dot f(t)\cdot g(t) \mathrm dt = \Big[f(t)\cdot g(t)\Big]_I - \int_I f(t)\cdot \dot g(t) \mathrm dt = -\int_I f(t)\cdot\dot g(t) \mathrm dt$

Si la distribution dérivée de f est encore d'un élément de L²(I,E), on dit qu'elle est dérivable au sens de Sobolev. Si cette dérivée est encore dérivable au sens précédent, on dit qu'elle est deux fois dérivables au sens de Sobolev. On note W^2,2(I,E) le sous-espace de L²(I,E) équipé du produit scalaire suivant <.,.>_W :

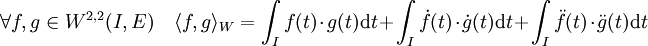
$\forall f,g \in W^{2,2}(I,E) \quad \langle f,g\rangle_W = \int_I f(t)\cdot g(t) \mathrm d t + \int_I \dot f(t)\cdot \dot g(t) \mathrm d t + \int_I \ddot f(t)\cdot \ddot g(t) \mathrm d t$

Les intégrales sont bien définies car elles correspondent au produit de deux élément de L²(I,E), il est ensuite simple de vérifier que l'espace est bien complet^[7]. Enfin, si f est une fonction dérivable au sens des distributions, il existe un représentant de f continue^[8]. Ainsi tout élément de W^2,2(I,E) admet un représentant continu et dont la dérivée admet aussi un représentant continu.

Équation d'Euler-Lagrange

Article détaillé : Équation d'Euler-Lagrange.

La difficulté est maintenant d'exprimer le gradient des fonctions Φ et Ψ. L'équation d'Euler-Lagrange cherche, dans un premier temps à trouver des fonctions de classe C² qui minimise Φ. L'espace vectoriel sous-jacent est celui des fonctions d'un intervalle borné et de classe C² et nulles aux bornes de l'intervalle. Sur cet espace, le calcul du gradient de Φ n'est guère complexe, il donne aussi une idée de la solution ainsi que de la méthode pour y parvenir. En revanche, ce calcul est insuffisant dans le cas présent. Avec le bon produit scalaire, l'espace des fonctions de classe C² n'est pas complet, ce qui empêche de disposer de la bonne géométrie permettant de démontrer la méthode du multiplicateur de Lagrange.

L'objectif est de généraliser un peu la démonstration pour permettre de disposer de l'égalité du gradient dans l'espace complet W^2,2(I,E). Dans un premier temps, exprimons l'égalité qui définit la différentielle de Φ en un point x, qui représente une fonction de W^2,2(I,E) :

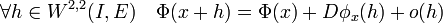
$\forall h \in W^{2,2}(I,E) \quad \Phi(x+h) = \Phi(x) + D\phi_x(h) + o(h)$

L'application DΦ_x est une application linéaire continue de W^2,2(I,E) dans R, c'est-à-dire un élément du dual topologique de W^2,2(I,E), que le produit scalaire permet d'identifier à W^2,2(I,E). L'égalité précédente devient :

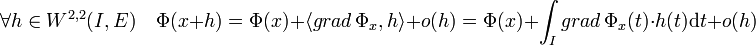
$\forall h \in W^{2,2}(I,E) \quad \Phi(x+h) = \Phi(x) + \langle grad \,\Phi_x, h\rangle + o(h) =\Phi(x) + \int_I grad \,\Phi_x(t)\cdot h(t) \mathrm d t + o(h)$

Autrement dit, le gradient de Φ au point x est une fonction de L²(I,E) dans R. De fait, ce gradient s'exprime à l'aide de l'équation d'Euler-Lagrange :

Le gradient de Φ au point x est la fonction de I dans E, définie par :

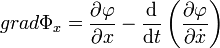
$grad \Phi_x = \frac{\partial \varphi}{\partial x}-\frac{\mathrm d}{ \mathrm dt}\left( \frac{\partial \varphi}{\partial \dot x} \right)$

Si la fonction φ est en général choisie au sens usuel de la dérivation, la fonction x(t) est une fonction de W^2,2(I,E). Le symbole d/dt doit être pris au sens de la dérivée d'une distribution, qui n'est ici nécessairement une fonction de carrée intégrable, définie presque partout.

Pour Ψ, la logique est absolument identique, mais cette fois-ci, la fonction est à valeurs dans F. En conséquence, la dérivée partielle de ψ par rapport à sa deuxième ou troisième variable n'est plus une application linéaire de E dans R, mais une application linéaire de E dans F. Ainsi, la différentielle de Ψ au point, une fonction x de I dans E, est une application de I dans L(E,F) l'ensemble des applications linéaires de E dans F. La logique reste la même.

La différentielle de Ψ au point x est la fonction de I dans L(E,F), définie par :

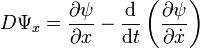$D \Psi_x = \frac{\partial \psi}{\partial x}-\frac{\mathrm d}{ \mathrm dt}\left( \frac{\partial \psi}{\partial \dot x} \right)$

Démonstration

L'application Φ est différentiable au point x, si x est une fonction de W^2,2(I,E) nulle aux bornes de I :

Cette proposition revient à montrer que :

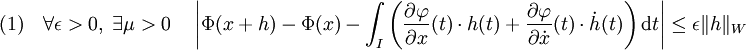
$(1)\quad \forall \epsilon >0,\;\exists \mu >0 \quad \left| \Phi(x+h) - \Phi(x) - \int_I \left(\frac {\partial \varphi}{\partial x}(t)\cdot h(t) + \frac {\partial \varphi}{\partial \dot x}(t)\cdot \dot h(t) \right)\mathrm d t\right| \le \epsilon \|h\|_W$

Soit ε un réel strictement positif. La fonction x et sa dérivée possède un représentant continu, dont les valeurs aux bornes de l'intervalle I sont nulles. En conséquence l'image de I par x et par sa dérivée est sont des compacts de E. Soit H le produit cartésien de I, x(I) et dx/dt(I). Le produit de trois compacts est encore un compact. La fonction différentielle de φ sur ce compact est uniformément continue, on en déduit, que les dérivée partielles à l'ordre 1 sont bornées par une valeur, notée M₁, on en déduit aussi, si a et b désigne les bornes de I :

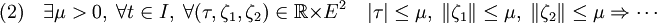
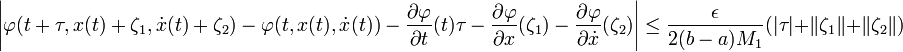
$(2)\quad \exists \mu >0 ,\;\forall t \in I,\; \forall (\tau,\zeta_1,\zeta_2) \in \mathbb R \times E^2 \quad |\tau| \le \mu,\; \|\zeta_1\|\le \mu,\;\|\zeta_2\|\le \mu \Rightarrow \cdots$ $\left|\varphi(t+\tau, x(t)+\zeta_1, \dot x(t) + \zeta_2) - \varphi(t,x(t),\dot x(t)) - \frac {\partial \varphi}{\partial t}(t)\tau - \frac {\partial \varphi}{\partial x}(\zeta_1) - \frac {\partial \varphi}{\partial \dot x}(\zeta_2)\right|\le \frac {\epsilon}{2(b-a)M_1}(|\tau| + \|\zeta_1\|+ \|\zeta_2\|)$

De plus, sur le compact H, la fonction |φ| ainsi que la norme de ses trois dérivées partielles atteint son maximum , notée M, car φ est continue. Si la norme de h dans W^2,2(I,E) est plus petite que μ², il existe un ensemble I_μ de I de mesure plus grande que b - a - ε.μ²/8M sur lequel h ainsi que sa dérivée ne dépasse pas μ. La majoration (2) montre que :

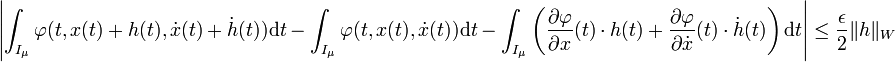
$\left|\int_{I_{\mu}}\varphi(t, x(t) + h(t), \dot x(t) + \dot h(t)) \mathrm dt - \int_{I_{\mu}}\varphi(t, x(t), \dot x(t)) \mathrm dt - \int_{I_{\mu}} \left(\frac {\partial \varphi}{\partial x}(t)\cdot h(t) + \frac {\partial \varphi}{\partial \dot x}(t)\cdot \dot h(t) \right)\mathrm d t\right| \le \frac {\epsilon}2\|h\|_W$

Sur le complémentaire de I_μ dans I, comme la fonction φ ne dépasse pas M en valeur absolue et comme le complémentaire est de mesure inférieure à ε.μ²/8M, on obtient :

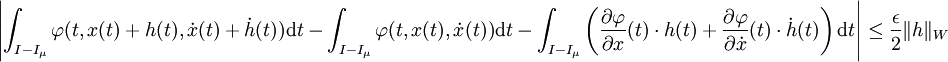
$\left|\int_{I-I_{\mu}}\varphi(t, x(t) + h(t), \dot x(t) + \dot h(t)) \mathrm dt - \int_{I-I_{\mu}}\varphi(t, x(t), \dot x(t)) \mathrm dt - \int_{I-I_{\mu}} \left(\frac {\partial \varphi}{\partial x}(t)\cdot h(t) + \frac {\partial \varphi}{\partial \dot x}(t)\cdot \dot h(t) \right)\mathrm d t\right| \le \frac {\epsilon}2\|h\|_W$

En sommant les deux dernières majorations, on trouve bien la majoration (1) qui montre la différentiabilité de Φ.

Le gradient de Φ au point x est donné par l'équation de Lagrange :

Une fois la proposition précédente démontrée, le reste du calcul est le même que celui de l'article Équation d'Euler-Lagrange. Le calcul consiste à exprimer différemment le gradient de Φ au point x :

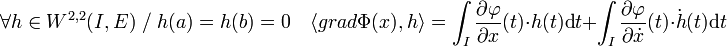
$\forall h \in W^{2,2}(I,E)\;/\; h(a) = h(b) = 0 \quad \langle grad \Phi(x),h\rangle = \int_I \frac {\partial \varphi}{\partial x}(t)\cdot h(t) \mathrm d t + \int_I \frac {\partial \varphi}{\partial \dot x}(t)\cdot \dot h(t)\mathrm d t$

Le fait que la fonction h soit nulle aux bornes de I et une intégration par parties montre que :

$\int_I \frac {\partial \varphi}{\partial \dot x}(t)\cdot \dot h(t)\mathrm d t =\left[\frac {\partial \varphi}{\partial \dot x}(t)\cdot h(t)\right]_a^b -\int_I \frac d{dt}\left(\frac {\partial \varphi}{\partial \dot x}(t)\right)\cdot h(t)\mathrm d t = -\int_I \frac d{dt}\left(\frac {\partial \varphi}{\partial \dot x}(t)\right)\cdot h(t)\mathrm d t$

Ce qui permet de déduire que :

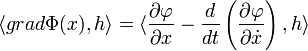
$\langle grad \Phi(x),h\rangle = \langle \frac {\partial \varphi}{\partial x} - \frac d{dt}\left(\frac {\partial \varphi}{\partial \dot x}\right),h\rangle$

Ce qui démontre la proposition. Les calculs sont exactement les mêmes pour la fonction Ψ.

Théorèmes

Ce paragraphe est très proche du précédent dans le cas de la dimension finie. Le problème à résoudre est de trouver le minimum suivant :

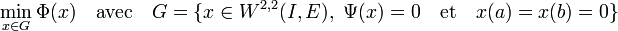
$\min_{x \in G} \Phi (x) \quad\text{avec}\quad G = \{x \in W^{2,2}(I,E),\; \Psi(x)=0\quad\text{et}\quad x(a) = x(b) = 0\}$

Théorème du multiplicateur de Lagrange — Si le point x₀ est un extremum local de Φ dans l'ensemble G, alors le noyau de la différentielle de Ψ au point x₀ est orthogonal au gradient de Φ en ce point.

On obtient les mêmes corollaire, que l'on peut écrire :

Corollaire — Si le point x₀ est un extremum local de Φ dans l'ensemble G et si la différentielle de Ψ au point x₀ est surjective, alors il existe un vecteur λ₀ de F tel que la fonction L de W^2,2(I,E)xF dans R admet un gradient nul en (x₀, λ₀) :

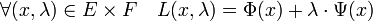
$\forall (x,\lambda) \in E\times F \quad L(x,\lambda) = \Phi(x) + \lambda \cdot \Psi (x)$

Cette équation s'écrit encore :

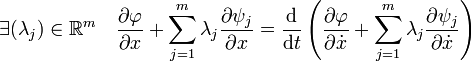
$\exists (\lambda_j) \in \mathbb R^m \quad \frac{\partial \varphi}{\partial x} + \sum_{j=1}^m \lambda_j \frac{\partial \psi_j}{\partial x} = \frac{\mathrm d}{ \mathrm dt}\left( \frac{\partial \varphi}{\partial \dot x} + \sum_{j=1}^m \lambda_j \frac{\partial \psi_j}{\partial \dot x} \right)$

Le signe d/dt doit être pris au sens de la dérivée des distributions. On obtient une solution faible, c'est-à-dire une fonction x définie presque partout et dérivable dans un sens faible. En revanche, si une fonction x de classe C² est solution du problème de minimisation, comme ses dérivées premières et secondes sont des représentants de ses dérivées au sens faible, L'équation précédente est encore vérifiée.

Démonstrations

La démonstration est proche de la précédente, néanmoins elle doit être adaptée au passage d'un espace euclidien à un hilbertien :

Cas où Ψ est une fonction affine :

La démonstration précédente n'utilise pas la dimension finie, elle s'applique donc encore de la même manière.

Cas général :

Une partie peut être reprise intégralement.

Première inégalité :

Elle consiste à utiliser la définition du gradient au point x₁, mais cette fois ci, valable pour tout vecteur de norme suffisamment petite, qui n'utilise pas la dimension finie :

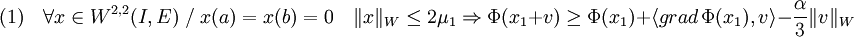
$(1)\quad \forall x \in W^{2,2}(I,E)\; /\; x(a) = x(b) = 0 \quad \|x\|_W \le 2\mu_1 \Rightarrow \Phi(x_1 + v) \ge \Phi (x_1) + \langle grad \,\Phi(x_1), v\rangle - \frac {\alpha}3\|v\|_W$

Deuxième inégalité :

La deuxième inégalité est démontrée, dans la démonstration précédente à l'aide de la dimension finie. Ici, on restreint nos ambitions pour uniquement montrer l'existence de deux nombres réels strictement positifs m et r tel que :

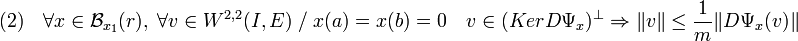
$(2)\quad \forall x \in \mathcal B_{x_1}(r),\; \forall v \in W^{2,2}(I,E)\; /\; x(a) = x(b) = 0 \quad v \in (Ker D\Psi_x)^{\bot} \Rightarrow \|v\| \le \frac 1m \|D\Psi_x(v)\|$

La démonstration reste néanmoins un peu analogue. Soit x un point de la boule de centre x₁ et de rayon 1. L'image de la différentielle de Ψ au point x et un espace vectoriel de dimension finie, le noyau est de codimension finie et son orthogonal de dimension finie. L'intersection de cet orthogonal avec la sphère unité est un compact, ce qui permet de définir les fonctions f et g comme pour le cas de la dimension finie. La continuité de g montre l'implication (2).

L'application, qui à x élément de W^2,2(I,E) associe DΨ_x est continue par hypothèse, ce qui ce traduit par :

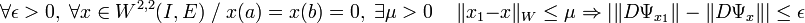
$\forall \epsilon > 0,\; \forall x \in W^{2,2}(I,E)\; /\; x(a) = x(b) = 0,\; \exists \mu > 0 \ \quad \|x_1 - x\|_W \le \mu \Rightarrow \left|\|D\Psi_{x_1}\| - \|D\Psi_{x}\| \right|\le \epsilon$

Soit v₁ (resp. v) un point de l'intersection de la sphère unité et de l'orthogonal du noyau de DΨ au point x₁ (resp. x), tel que :

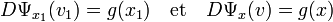
$D\Psi_{x_1}(v_1) = g(x_1)\quad\text{et}\quad D\Psi_{x}(v) = g(x)$

La continuité de la différentielle montre :

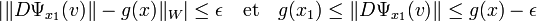
$\left| \|D\Psi_{x_1}(v)\| - g(x)\|_W \right| \le \epsilon\quad\text{et}\quad g(x_1) \le \|D\Psi_{x_1}(v)\| \le g(x) - \epsilon$

Les mêmes majorations montrent que :

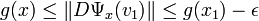
$g(x) \le \|D\Psi_{x}(v_1)\| \le g(x_1) - \epsilon$

Ce qui montre la continuité de g et par voie de conséquence la majoration (2), il suffit de choisir m comme l'inverse de la valeur g(x₁).

Troisième et quatrième inégalités :

La troisième inégalité ne fait pas appel à la dimension finie, on l'a rappelle dans le nouveau contexte :

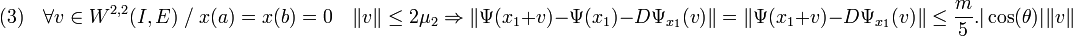
$(3)\quad \forall v \in W^{2,2}(I,E)\; /\; x(a) = x(b) = 0 \quad \|v\| \le 2\mu_{2} \Rightarrow \|\Psi(x_1 + v) - \Psi(x_1) - D\Psi_{x_1}(v)\| = \|\Psi(x_1 + v) - D\Psi_{x_1}(v)\| \le \frac m5.|\cos (\theta)| \|v\|$

Il en est de même pour la quatrième inégalité :

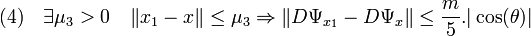
$(4)\quad \exists \mu_3 >0 \quad \|x_1 - x \|\le \mu_3 \Rightarrow \|D\Psi_{x_1} - D\Psi_x\|\le \frac m5.|\cos (\theta)|$

Conclusion :

La conclusion est la même, il suffit maintenant de choisir μ non seulement plus petit que μ₁, μ₂ et μ₃ mais aussi plus petit que r.

Application : Théorème isopérimétrique

Article détaillé : Théorème isopérimétrique.

En répartissant uniformément la courbure de la frontière on obtient l'optimal isopérimétrique.

On recherche la surface de plus grande aire, ayant une frontière de longueur égale à 2π. On remarque que la surface est nécessairement convexe, d'intérieur non vide. On considère une droite coupant la surface en deux. Cette droite est utilisée comme axe d'un repère orthonormal, dont les abscisses sont notées par la lettre t et les ordonnées par x. La frontière supérieure est paramétrable en une courbe x(t) et, si le repère est bien choisi, on peut prendre comme abscisse minimale -a et maximale a. On recherche alors une courbe x, définie entre -a et a tel que l'aire A soit maximale :

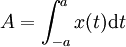
$A = \int_{-a}^a x(t) \mathrm dt$

On sait de plus que la demi longueur de la frontière est égale à π :

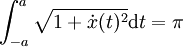
$\int_{-a}^a \sqrt {1 + \dot x(t)^2}\mathrm dt = \pi$

La recherche de la surface se traite aussi avec le multiplicateur de Lagrange. La même astuce que celle utilisée dans l'exemple introductif montre, avec les notations usuelles :

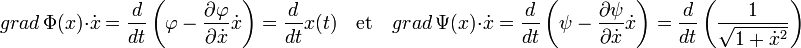
$grad \,\Phi(x)\cdot \dot x = \frac d{dt}\left(\varphi -\frac {\partial \varphi}{\partial \dot x}\dot x\right) =\frac d{dt} x(t)\quad\text{et}\quad grad \,\Psi(x)\cdot \dot x = \frac d{dt}\left(\psi -\frac {\partial \psi}{\partial \dot x}\dot x\right) = \frac d{dt}\left(\frac 1{\sqrt{1+ \dot x^2}}\right)$

On en déduit l'existence de valeurs λ et k tel que :

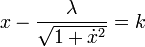
$x - \frac {\lambda}{\sqrt{1+ \dot x^2}}=k$

En notant u = x - k, on obtient :

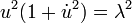
$u^2(1+ \dot u^2) =\lambda^2$

On trouve l'équation d'un demi-cercle de rayon λ, la valeur λ est égale à 1 et k à 0.^[9]

Voir aussi

Notes

↑ Ce résultat est énoncé sous une forme équivalente mais moins général dans : D. Hoareau Cauchy-Schwarz par le calcul différentiel MégaMaths sur ifrance (2003)
↑ On trouve ce corollaire dans : D. Klein Lagrange Multipliers without Permanent Scarring University of California at Berkeley
↑ Voir par exemple : M. Bierlaire Multiplicateur de Lagrange Ecole polytechnique fédérale de Lausanne
↑ Elle est explicitée dans l'article : D. Hoareau Cauchy-Schwarz par le calcul différentiel MégaMaths sur ifrance (2003)
↑ Cet exemple est extrait de : X. Gourdon Analyse, Les maths en tête : Mathématiques pour MP* Ellipses Marketing 2^ième édition (2008) (ISBN 2729837590)
↑ Cet exemple est traité dans : C Barreteau Calcul des variations Ecole supérieure de physique et de chimie industrielle
↑ Pour plus de détails voir : L Andry Les espaces de Sobolev Ecole polytechnique fédérale de Lausanne
↑ Théorème VIII.2 p 122 Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
↑ Ce calcul est présenté, par exemple sur : S. Mehl Didon, Carthage, calcul des variations et multiplicateur de Lagrange Chronomath.com

Liens externes

(fr) D. Hoareau Cauchy-Schwarz par le calcul différentiel sur ifrance.com
(fr) La méthode du Lagrangien École des Hautes Études Commerciales Montréal Québec (1999)
(fr) Extrema liés - Multiplicateurs de Lagrange sur BibM@th
(en) D. Klein Lagrange Multipliers without Permanent Scarring Université de Berkeley

Références

(fr) X. Gourdon Analyse, Les maths en tête : Mathématiques pour MP* Ellipses Marketing 2^ième édition (2008) (ISBN 2729837590)
(fr) Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
(en) W. P. Ziemer Weakly Differentiable Functions: Sobolev Spaces and Functions of Bounded Variation Springer (1989) (ISBN 0387970177)

Portail des mathématiques

Ce document provient de « Multiplicateur de Lagrange ».

Catégories : Calcul des variations | Optimisation | Joseph-Louis Lagrange

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Multiplicateur de lagrange de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Multiplicateur De Lagrange — Pour les articles homonymes, voir Théorème de Lagrange. La méthode des multiplicateurs de Lagrange permet de trouver un optimum, sur la figure le point le … Wikipédia en Français
Multiplicateur de Lagrange — Pour les articles homonymes, voir Théorème de Lagrange. La méthode des multiplicateurs de Lagrange permet de trouver un optimum, sur la figure le point le plus élevé possible, tout en satisfaisant une contrainte, sur la figure un … Wikipédia en Français
multiplicateur de Lagrange — Lagranžo daugiklis statusas T sritis fizika atitikmenys: angl. Lagrangian multiplier vok. Lagrange Faktor, m rus. множитель Лагранжа, m pranc. multiplicateur de Lagrange, m … Fizikos terminų žodynas
Lagrange — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronymes 1.1 Lagrange 1.2 … Wikipédia en Français
Lagrange-Faktor — Lagranžo daugiklis statusas T sritis fizika atitikmenys: angl. Lagrangian multiplier vok. Lagrange Faktor, m rus. множитель Лагранжа, m pranc. multiplicateur de Lagrange, m … Fizikos terminų žodynas
Joseph-Louis Lagrange — Pour les articles homonymes, voir Lagrange. Joseph Louis Lagrange Naissance … Wikipédia en Français
Joseph-Louis de Lagrange — Joseph Louis Lagrange Pour les articles homonymes, voir Lagrange. Joseph Louis Lagrange … Wikipédia en Français
Joseph-louis lagrange — Pour les articles homonymes, voir Lagrange. Joseph Louis Lagrange … Wikipédia en Français
Joseph Louis Lagrange — Pour les articles homonymes, voir Lagrange. Joseph Louis Lagrange … Wikipédia en Français
Théorème de Lagrange — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Pour les articles homonymes, voir Lagrange. Le théorème de Lagrange sur les sous groupes en algèbre est un résultat élémentaire concernant les groupes… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Multiplicateur de lagrange