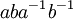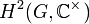Multiplicateur de schur

Multiplicateur de schur

Multiplicateur de Schur

En mathématiques, plus précisément en théorie des groupes, le multiplicateur de Schur, nommé en l'honneur de Issai Schur, est le deuxième groupe d'homologie d'un groupe G avec des coefficients dans les entiers,

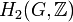H_2(G, {\Bbb Z})\,.

Si le groupe est présenté en termes d'un groupe libre F sur un ensemble de générateurs, et un sous-groupe normal R engendré par un ensemble de relations sur les générateurs, de sorte que

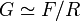G \simeq F/R,

alors par la formule intégrale d'homologie de Hopf, nous avons le multiplicateur de Schur

(R \cap [F, F])/[F, R],

où [A, B] est le groupe engendré par les commutateurs

aba^{-1}b^{-1}\,

pour a dans A et b dans B. Il peut aussi être exprimé en termes de cohomologie, comme

H^2(G, \Bbb{C}^\times)

où G agit trivialement sur le groupe multiplicatif des nombres complexes différents de zéro.

Les multiplicateurs de Schur sont d'un intérêt particulier lorsque G est un groupe parfait (un groupe égal à son propre sous-groupe de commutateur). Un groupe parfait possède une seule extension centrale parfaite maximale, ou groupe universel de revêtement, dont le centre contient le multiplicateur de Schur et dont le quotient par celui-ci est le groupe parfait.

Le multiplicateur de Schur est dû à Issai Schur, et peut être dit représenter le début de la cohomologie de groupe (ou au moins des groupes plus hauts que H2 etc.).

Références

  • Karpilovsky, Gregory: The Schur Multiplier, Oxford University Press, 1987, ISBN 0-19-853554-6.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Multiplicateur de Schur ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Multiplicateur de schur de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Multiplicateur De Schur — En mathématiques, plus précisément en théorie des groupes, le multiplicateur de Schur, nommé en l honneur de Issai Schur, est le deuxième groupe d homologie d un groupe G avec des coefficients dans les entiers, . Si le groupe est présenté en… …   Wikipédia en Français

  • Multiplicateur de Schur — En mathématiques, plus précisément en théorie des groupes, le multiplicateur de Schur est le deuxième groupe d homologie d un groupe G à coefficients entiers, . Si le groupe est présenté en termes d un groupe libre F sur un ensemble de… …   Wikipédia en Français

  • Issai Schur — Issai Schur, né à Moguilev le 10 janvier 1875 et mort à Tel Aviv le 10 janvier 1941, est un mathématicien russe qui a surtout travaillé en Allemagne. Il a étudié à Berlin sous Frobenius, a obtenu son doctorat en 1901 et est… …   Wikipédia en Français

  • Groupes finis simples — Liste des groupes finis simples En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe …   Wikipédia en Français

  • Liste Des Groupes Finis Simples — En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe de Tits), soit l un des 26… …   Wikipédia en Français

  • Liste des groupes finis simples — En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe de Tits), soit l un des 26… …   Wikipédia en Français

  • Groupe De Type De Lie — En mathématiques, un groupe de type de Lie G(k) est un groupe (non nécessairement fini) de points rationnels d un groupe algébrique linéaire G à valeur dans le corps k. La classification des groupes simples finis montre que les groupes de types… …   Wikipédia en Français

  • Groupe de type de Lie — En mathématiques, un groupe de type de Lie G(k) est un groupe (non nécessairement fini) de points rationnels d un groupe algébrique linéaire réductif (en) G à valeur dans le corps commutatif k. La classification des groupes simples finis… …   Wikipédia en Français

  • Groupe de type de lie — En mathématiques, un groupe de type de Lie G(k) est un groupe (non nécessairement fini) de points rationnels d un groupe algébrique linéaire G à valeur dans le corps k. La classification des groupes simples finis montre que les groupes de types… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”