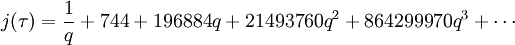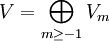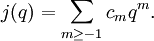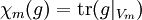Conjecture Monstrous Moonshine

Conjecture Monstrous Moonshine

Monstrous moonshine

En mathématiques, monstrous moonshine est un terme anglais conçu par John Horton Conway et Simon P. Norton en 1979, utilisé pour décrire la connexion (alors totalement inattendue) entre le groupe Monstre M et les fonctions modulaires (particulièrement, la ).

Précisément, Conway et Norton, suivant une observation initiale de John McKay, trouvèrent que le développement de Fourier de 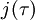j(\tau)\, (OEIS A000521, avec 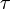\tau\, désignant le ratio de demi-période) pouvait être exprimé en termes de combinaisons linéaires des dimensions des représentations irréductibles de M (OEIS A001379)

j(\tau) = \frac{1}{{q}} + 744 + 196884{q} + 21493760{q}^2 + 864299970{q}^3 + \cdots

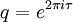où {q} = e^{2\pi i\tau}\, et

1 \,\! = \,\! 1 \,\!
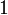
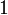
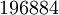
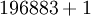
196884 \,\! = \,\! 196883 + 1 \,\!
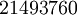
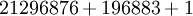
21493760 \,\! = \,\! 21296876 + 196883 + 1 \,\!
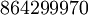
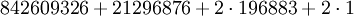
864299970 \,\! = \,\! 842609326 + 21296876 + 2\cdot 196883 + 2\cdot 1 \,\!
align="right" | 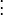\vdots

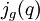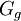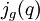Conway et Norton formulèrent des conjectures concernant les fonctions j_g({q})\, obtenues en remplaçant les traces sur l'identité par les traces sur d'autres éléments g de M. La partie la plus saisissante de ces conjectures est que toutes ces fonctions sont de genre zéro. En d'autres termes, si G_g\, est le sous-groupe de SL2(\mathbb{R}) qui fixe j_g({q})\,, alors le quotient du demi-plan supérieur du plan complexe par 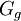G_g\, est une sphère avec un nombre fini de point enlevés, correspondant aux formes paraboliques de G_g\,.

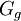Il s'avère que derrière monstrous moonshine se trouve une certaine théorie des cordes ayant le groupe Monstre comme symétries; les conjectures faites par Conway et Norton furent démontrées par Richard Ewen Borcherds en 1992 en utilisant le théorème sans fantôme à partir de la théorie des cordes, de la théorie des algèbres vertex et des superalgèbres généralisées de Kac-Moody. Borcherds reçu la médaille Fields pour son travail, et plus de connexions entre M et la fonction j furent découvertes ultérieurement.

Sommaire

Versions formelles des conjectures de Conway et Norton

La première conjecture faite par Conway et Norton fut ce que l'on appela la "conjecture moonshine"; elle établit qu'il existe un M-module gradué de dimension infinie

V = \bigoplus_{m\geq -1} V_m

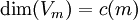avec \dim(V_m) = c(m) pour tout m, où

j({q}) = \sum_{m\geq -1} c_m {q}^m.

De ceci, il s'ensuit que chaque élément g de M agit sur chaque Vm et possède une valeur de caractère

\chi_m(g) = \mathrm{tr}(g|_{V_m})

qui peut être utilisée pour construire la série de McKay-Thompson de g :

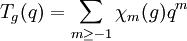T_g({q}) = \sum_{m\geq -1} \chi_m(g){q}^m.

La deuxième conjecture de Conway et Norton établit ensuite qu'avec V comme ci-dessus, pour chaque élément g de M, il existe un sous-groupe de genre zéro K de 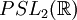PSL_2(\mathbb{R})\,, commensurable avec le groupe modulaire Γ :

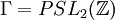\Gamma = PSL_2(\mathbb{Z})\,, tel que 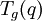T_g({q})\, est la fonction modulaire principale normalisée pour K.

Le module Monstre

Il fut montré plus tard par A. Oliver L. Atkin, Paul Fong et Frederic L. Smith en utilisant des calculs informatiques qu'il existe en effet une représentation graduée de dimension infinie du groupe Monstre dont les séries de McKay-Thompson sont précisément les Hauptmoduls trouvés par Conway et Norton, I. B. Frenkel, J. Lepowsky et A. Meurman construisirent explicitement cette représentation en utilisant les opérateurs vertex. Le module résultant est appelé le module Monstre.

La démonstration de Borcherds

La démonstration de Richard Ewen Borcherds de la conjecture de Conway et Norton peut être séparée en cinq étapes majeures comme ce qui suit :

  1. Une algèbre vertex V est construite, c’est-à-dire une algèbre graduée pouvant effectuer les représentation moonshine sur M, et il est vérifié que le module Monstre possède une structure d'algèbre vertex invariante sous l'action de M. V est ainsi appelée l'algèbre vertex Monstre.
  2. Une algèbre de Lie 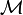\mathcal{M}\, est construite à partir de V en utilisant le théorème "sans fantôme" de Goddard-Thorn à partir de la théorie des cordes; ceci est une algèbre de Lie Kac-Moody généralisée.
  3. Un dénominateur identité pour 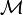\mathcal{M} est construit, c’est-à-dire relié aux coefficients de j({q})\,.
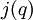  4. Un nombre de dénominateurs identités tordus sont construits qui sont reliés de manière similaire aux séries T_g({q})\,.
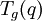  5. Les dénominateurs identités sont utilisés pour déterminer les nombres cm, utilisant les opérateurs de Hecke, l'homologie d'algèbre de Lie et les opérations d'Adams.

Ainsi, la démonstration est complétée. Borcherds fut plus tard cité comme ayant dit "j'étais sur la Lune lorsque j'ai démontré la conjecture moonshine (clair de lune)", et "Je me demande quelquefois si c'est ce que l'on ressend lorsque l'on prend certaines drogues. Je ne le sais pas actuellement, comme je n'ai pas testé cette théorie sur moi."

Pourquoi « monstrous moonshine » ?

Le terme « monstrous moonshine » fut inventé par Conway, qui, lorsque John McKay lui dit à la fin des années 1970 que les coefficients de q (concrêtement 196 884) étaient précisément la dimension de l'algèbre de Griess (et ainsi exactement un de plus que le degré de la plus petite représentation fidèle complexe du groupe Monstre), répondit que ceci était « moonshine » (au sens de « dingue » ou « idées folles »). Ainsi, le terme fait référence non seulement au groupe Monstre M; il fait aussi référence à la folie perçue concernant la relation compliquée entre M et la théorie des fonctions modulaires.

Cependant, « moonshine » est aussi un mot d'argot pour un whiskey distillé illégalement, et en fait, le nom peut être expliqué à la lumière de ceci. Le groupe Monstre fut étudié dans les années 1970 par les mathématiciens Fricke, Andrew Ogg et John G. Thompson; ils étudièrent le quotient du plan hyperbolique par les sous-groupes de 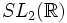SL_2(\mathbb{R})\,, particulièrement, le normalisateur 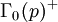\Gamma_0(p)^+\, de (p) dans SL(2,R). Ils trouvèrent que la surface de Riemann résultant en prenant le quotient du plan hyperbolique par 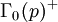\Gamma_0(p)^+\, est de genre zéro ssi p est 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59 ou 71 (c’est-à-dire, un nombre premier super-singulier), et lorsque Ogg entendit plus tard parler du groupe Monstre et nota que ces nombres étaient précisément les facteurs premiers de la taille de M, il prépara un papier offrant une bouteille de whiskey Jack Daniel's à quiconque pouvait expliquer ce fait.

Références

  • John Horton Conway and Simon P. Norton, Monstrous Moonshine, Bull. London Math. Soc. 11, 308–339, 1979.
  • I. B. Frenkel, J. Lepowsky, and A. Meurman, Vertex Operator Algebras and the Monster, Pure and Applied Math., Vol. 134, Academic Press, 1988
  • Richard Ewen Borcherds, Monstrous Moonshine and Monstrous Lie Superalgebras, Invent. Math. 109, 405–444, 1992, online
  • Terry Gannon, Monstrous Moonshine: The first twenty-five years, 2004, online
  • Terry Gannon, Monstrous Moonshine and the Classification of Conformal Field Theories, reprinted in Conformal Field Theory, New Non-Perturbative Methods in String and Field Theory, (2000) Yavuz Nutku, Cihan Saclioglu, Teoman Turgut, eds. Perseus Publishing, Cambridge Mass. ISBN 0-7382-0204-5 (Provides introductory reviews to applications in physics).

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Monstrous moonshine ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conjecture Monstrous Moonshine de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Monstrous moonshine — En mathématiques, monstrous moonshine est un terme anglais conçu par John Horton Conway et Simon P. Norton (en) en 1979, utilisé pour décrire la connexion (alors totalement inattendue) entre le groupe Monstre M et les fonctions modulaires… …   Wikipédia en Français

  • Monstrous moonshine — In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the (then totally unexpected) connection between the monster group M and modular functions… …   Wikipedia

  • Groupe Monstre —  Pour l’article homonyme, voir Groupe monstre de Tarski (en).  En mathématiques, le Monstre M ou groupe de Fischer Griess F1 est le plus gros des 26 groupes simples …   Wikipédia en Français

  • Groupes finis simples — Liste des groupes finis simples En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe …   Wikipédia en Français

  • Liste Des Groupes Finis Simples — En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe de Tits), soit l un des 26… …   Wikipédia en Français

  • Liste des groupes finis simples — En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe de Tits), soit l un des 26… …   Wikipédia en Français

  • List of conjectures — This is an incomplete list of mathematical conjectures. They are divided into four sections, according to their status in 2007. See also: * Erdős conjecture, which lists conjectures of Paul Erdős and his collaborators * Unsolved problems in… …   Wikipedia

  • Algèbre de Lie — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d un crochet de Lie, c est à dire d une loi de composition interne… …   Wikipédia en Français

  • Beaute mathematique — Beauté mathématique La frontière de l ensemble de Mandelbrot. Certains mathématiciens recherchent dans leur travail ou dans les mathématiques en général, un plaisir esthétique. Ils expriment ce plaisir en décrivant de « belles » parties …   Wikipédia en Français

  • Beauté Mathématique — La frontière de l ensemble de Mandelbrot. Certains mathématiciens recherchent dans leur travail ou dans les mathématiques en général, un plaisir esthétique. Ils expriment ce plaisir en décrivant de « belles » parties des mathématiques.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”