Groupe De Mathieu

Groupe De Mathieu

Groupe de Mathieu

En mathématiques, les groupes de Mathieu sont cinq groupes simples finis découverts par le mathématicien français Emile Léonard Mathieu. Ils sont habituellement perçus comme des groupes de permutation sur n points (où n peut prendre les valeurs 11, 12, 22, 23 ou 24) et sont nommés M_n\,.

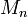Les groupes de Mathieu ont été les premiers groupes sporadiques découverts.

Sommaire

Groupes multiplement transitifs

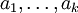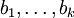Les groupes de Mathieu sont des exemples de groupes multiplement transitifs. Pour un nombre naturel k, un groupe de permutation G agissant sur n points est k-transitif si, étant donné deux ensembles de points a_1,\ldots,a_k\, et b_1,\ldots,b_k\, avec la propriété que tous les ai sont distincts et que tous les bi sont distincts, il existe un élément de groupe g dans G qui applique ai vers bi pour chaque i entre 1 et k. Un tel groupe est appelé fortement k-transitif[1] si l'élément g est unique (i.e. l'action sur les k-uplets est régulière, et non seulement transitive).

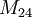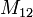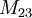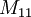Les groupes M_{24}\, et M_{12}\, sont 5-transitifs, les groupes M_{23}\, et M_{11}\, sont 4-transitifs et 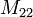M_{22}\, est 3-transitif.

Il résulte de la classification des groupes simples finis que les seuls groupes qui sont k-transitifs pour k au moins égal à 4 sont le groupe symétrique et les groupes alternés (de degré k et k-2 respectivement) et les groupes de Mathieu 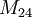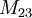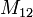M_{24}\,, M_{23}\,, M_{12}\, et M_{11}\,.

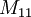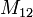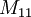C'est un résultat classique de Jordan que le groupe symétrique et les groupes alternés (de degrés k et k - 2 respectivement), M_{12}\, et M_{11}\, sont les seuls groupes de permutation fortement k-transitifs pour k égal au moins à 4.

Ordres

Groupe Ordre Ordre factorisé
M24 244 823 040 210.33.5.7.11.23
M23 10 2009 60 27.32.5.7.11.23
M22 443 520 27.32.5.7.11
M12 95 040 26.33.5.11
M11 7 920 24.32.5.11

Deux constructions des groupes de Mathieu

Groupe d'automorphisme des systèmes de Steiner

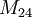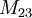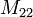Il existe, à une équivalence près, un unique système de Steiner S(5,8,24). Le groupe M_{24}\, est le groupe d'automorphisme de ce système de Steiner; c’est-à-dire, l'ensemble des permutations qui applique chaque bloc vers un certain autre bloc. Les sous-groupes M_{23}\, et M_{22}\, sont définis comme étant les stabilisateurs d'un seul point et de deux points respectivement.

De manière similaire, il existe, à une équivalence près, un unique système de Steiner S(5,6,12) et le groupe 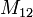M_{12}\, est son groupe d'automorphisme. Le sous-groupe 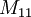M_{11}\, est le stabilisateur d'un point.

Pour une introduction d'une construction de 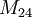M_{24}\, comme groupe d'automorphisme de S(5,8,24) via le Générateur d'Octade Miraculeux de R. T. Curtis, voir Géométrie du carré 4x4. Un autre bon accès à ceci et à l'analogue de Conway pour S(5,6,12), le miniGOM, peut être trouvé dans le livre de Conway et Sloane.

Une construction alternative de S(5,6,12) est le Chaton de R.T. Curtis.

Groupe d'automorphisme du code de Golay

Le groupe 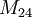M_{24}\, peut aussi être vu comme le groupe d'automorphisme du code binaire de Golay W, i.e., le groupe des permutations de coordonnées appliquant W vers lui-même. Nous pouvons aussi le regarder comme l'intersection de 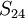S_{24}\, et Stab(W) dans Aut(V). Les mots code correspondent de manière naturelle aux sous-ensembles d'un ensemble de 24 objets. Ces sous-ensembles correspondant aux mots code à 8 ou 12 coordonnées égales à 1 sont appelés octades ou dodécades respectivement. Les octades sont des blocs d'un système de Steiner S(5,8,24).

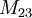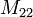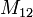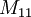Les sous-groupes simples M_{23}\,, M_{22}\,, M_{12}\, et M_{11}\, peuvent être définis comme des sous-groupes de 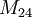M_{24}\,, stabilisateurs respectivement de coordonnée unique, une paire ordonnée de coordonnées, une paire de dodécades complémentaires et une paire de dodécade avec une coordonnée seule.

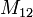M_{12}\, possède un index 2 dans son groupe d'automorphisme. Comme un sous-groupe de 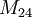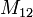M_{24}\,, M_{12}\, agit sur la deuxième dodécade comme une image d'automorphisme extérieur de son action sur la première dodécade. 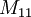M_{11}\, est un sous-groupe de 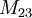M_{23}\, mais pas de 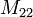M_{22}\,. Cette représentation de 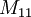M_{11}\, possède des orbites de 11 et 12. Le groupe d'automorphisme de 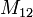M_{12}\, est un sous-groupe maximal de 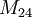M_{24}\, d'index 1288.

Il existe une connexion très naturelle entre les groupes de Mathieu et les groupes de Conway plus grands parce que le code binaire de Golay et le réseau de Leech se trouvent tous deux dans des espaces à 24 dimensions. Les groupes de Conway se retrouvent à leur tour dans le groupe Monstre. Robert Griess fait référence aux 20 groupes sporadiques trouvés dans le Monstre comme la famille heureuse et aux groupes de Mathieu comme la première génération.

Liens externes

  • Moggie Applet Java pour étudier la construction GOM de Curtis.

Bibliographie

  • Mathieu É., Mémoire sur l’étude des fonctions de plusieurs quantités, sur la manière de les former et sur les substitutions qui les laissent invariables, Journal de mathématiques pures et appliquées (Journal de Liouville), 1861, pp. 241 et ss.
  • Mathieu É., Sur la fonction cinq fois transitive de 24 quantités, Journal de mathématiques pures et appliquées (Journal de Liouville), (2) XVIII., 1873, pp. 25-47.
  • Conway, J. H.; Curtis, R. T.; Norton, S. P.; Parker, R. A.; Wilson, R. A. (1985). Atlas of finite groups. Maximal subgroups and ordinary characters for simple groups. With computational assistance from J. G. Thackray. Eynsham: Oxford University Press. ISBN 0-19-853199-0
  • Conway, J.H.; Sloane N.J.A. Sphere Packings, Lattices and Groups: v. 290 (Grundlehren Der Mathematischen Wissenschaften.) Springer Verlag. ISBN 0-387-98585-9
  • Curtis, R. T. A new combinatorial approach to M24. Math. Proc. Camb. Phil. Soc. 79 (1976) 25-42.
  • Thompson, Thomas M.: "From Error Correcting Codes through Sphere Packings to Simple Groups", Carus Mathematical Monographs, Mathematical Association of America, 1983.
  • Curtis, R. T. "The Steiner System S(5,6,12), the Mathieu Group M12 and the 'Kitten' ," Computational Group Theory, Academic Press, London, 1984
  • Griess, Robert L.: "Twelve Sporadic Groups", Springer-Verlag, 1998.

Notes et références

  1. ↑ Jacques Tits, « Groupes finis simples sporadiques » (Séminaire Bourbaki, 22e année, 1969/70, n° 375), section 1.2.3, p. 191, dit « fortement n fois transitif ». Voyez en ligne.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Groupe de Mathieu ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe De Mathieu de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Groupe de mathieu — En mathématiques, les groupes de Mathieu sont cinq groupes simples finis découverts par le mathématicien français Emile Léonard Mathieu. Ils sont habituellement perçus comme des groupes de permutation sur n points (où n peut prendre les valeurs… …   Wikipédia en Français

  • Groupe de Mathieu — En mathématiques, les groupes de Mathieu sont cinq groupes simples finis découverts par le mathématicien français Émile Mathieu. Ils sont habituellement perçus comme des groupes de permutation sur n points (où n peut prendre les valeurs 11, 12,… …   Wikipédia en Français

  • Groupe Sporadique — En mathématiques, un groupe sporadique est l un des 26 groupes exceptionnels dans la classification des groupes simples finis. Un groupe simple est un groupe G qui ne possède aucun sous groupe normal à part le sous groupe trivial réduit à l… …   Wikipédia en Français

  • Groupe (mathématique) — Groupe (mathématiques) Pour les articles homonymes, voir Groupe.  Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes …   Wikipédia en Français

  • Groupe De Higman-Sims — En mathématiques, le groupe de Higman–Sims est un groupe sporadique simple fini d ordre 44 352 000. Il peut être caractérisé comme le sous groupe simple d index 2 dans le groupe des automorphismes du graphe de Higman–Sims. Le graphe de… …   Wikipédia en Français

  • Groupe de higman-sims — En mathématiques, le groupe de Higman–Sims est un groupe sporadique simple fini d ordre 44 352 000. Il peut être caractérisé comme le sous groupe simple d index 2 dans le groupe des automorphismes du graphe de Higman–Sims. Le graphe de… …   Wikipédia en Français

  • Groupe De Held — En mathématiques, le groupe de Held, , est l unique groupe sporadique simple fini d ordre . Il peut être défini en termes de générateurs a et b et de relations : . Il a été …   Wikipédia en Français

  • Groupe de held — En mathématiques, le groupe de Held, , est l unique groupe sporadique simple fini d ordre . Il peut être défini en termes de générateurs a et b et de relations : . Il a été …   Wikipédia en Français

  • Groupe sporadique — En mathématiques, un groupe sporadique est l un des 26 groupes exceptionnels dans la classification des groupes simples finis. Un groupe simple est un groupe G non trivial qui ne possède aucun sous groupe normal à part son sous groupe trivial… …   Wikipédia en Français

  • Groupe (mathématiques) — Pour les articles homonymes, voir Groupe. Les manipulations possibles du cube de Rubik forment un groupe. En mathématiques, un groupe est un ensemble …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”