- Algebre vertex
-
Algèbre vertex
En mathématiques, une algèbre vertex est une structure algébrique qui joue un rôle important en théorie conforme des champs et dans les domaines proches en physique. Ces structures ont aussi montré leur utilité en mathématiques dans des contextes comme l'étude du groupe Monstre et la correspondance de Langlands géométrique.
Les algèbres vertex ont été introduites par Richard Borcherds en 1986, motivées par les opérateurs vertex intervenant lors de l'insertion de champs, dans la théorie conforme des champs en dimension 2. Comme exemples importants, on peut citer les algèbres vertex associées aux réseaux, celle provenant des modules sur les algèbres de Kac-Moody, celles provenant de l'algèbre de Virasoro et enfin le module moonshine V♮ construit par Frenkel, Lepowsky et Meurman en 1988.
Les axiomes des algèbres vertex sont une version algébrique de ce que les physiciens appellent une algèbre chirale, dont la définition rigoureuse a été donnée par Beilinson et Drinfeld.
Définition
Une algèbre vertex est un espace vectoriel V, muni d'un élément unité 1, d'un endomorphisme T et d'une application de multiplication
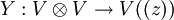 qu'on écrit
qu'on écrit 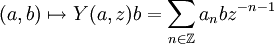
vérifiant les axiomes suivants :
- (Identité) Pour tout
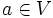 ,
,
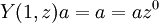 et
et ![Y(a,z)1 \in a + zV[[z]]\,](/pictures/frwiki/100/d838694e24fc6abd75a74ad30df9a1d8.png)
- (Translation) T(1) = 0, et pour tous
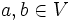 ,
,
- (4 points) Pour tous
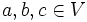 , il existe un élément
, il existe un élément
![X(a,b,c;z,w) \in V[[z,w]][z^{-1}, w^{-1}, (z-w)^{-1}]](/pictures/frwiki/98/b82778a4f6d0fdbd74084e07e7a0d093.png)
- tel que Y(a,z)Y(b,w)c, Y(b,w)Y(a,z)c, et Y(Y(a,z-w)b,w)c sont les expansions de X(a,b,c;z,w) dans V((z))((w)), V((w))((z)), et V((w))((z-w)), respectivement.
L'application de multiplication est souvent vue comme une correspondance entre états et champs
associant une distribution formelle à coefficient opérateurs (un opérateur vertex) à chaque vecteur. Physiquement, la correspondance est une insertion à l'origine et T est un générateur infinitésimal des translations. L'axiome des 4 points mélange l'associativité et la commutativité, aux singularités près.
Remarque : l'axiome de translation entraîne que Ta = a-21, donc T est uniquement déterminé par Y.
Une algèbre vertex V est Z+-graduée si
et si a ∈ Vk et b ∈ Vm implique an b ∈ Vk+m-n-1.
Une algèbre vertex conforme est une algèbre vertex Z+-graduée munie d'un élément de Virasoro ω ∈ V2, tel que l'opérateur vertex associé
vérifie, pour tout a ∈ Vn, les relations :
où c est une constante appelée la charge centrale ou le rang de V. En particulier, ceci munit V d'une action de l'algèbre de Virasoro.
Références
- Richard Borcherds, "Vertex algebras, Kac-Moody algebras, and the Monster", Proc. Natl. Acad. Sci. USA. 83 (1986) 3068-3071
- Igor Frenkel, James Lepowsky, Arne Meurman, "Vertex operator algebras and the Monster". Pure and Applied Mathematics, 134. Academic Press, Inc., Boston, MA, 1988. liv+508 pp. ISBN 0-12-267065-5
- Edward Frenkel, David Ben-Zvi, "Vertex algebras and Algebraic Curves". Mathematical Surveys and Monographs, 88. American Mathematical Society, 2001. xii+348 pp. ISBN 0-8218-2894-0
- Portail des mathématiques
Catégorie : Algèbre
Wikimedia Foundation. 2010.

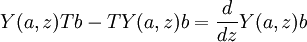
![Y: V \to (End V)[z^{\pm 1}]](/pictures/frwiki/102/fddca2f06b94b74a3f2f96c8b750c08f.png)
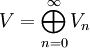
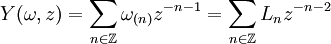
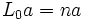
![Y(L_{-1} a, z) = \frac{d}{dz} Y(a, z) = [Y(a,z),T]\,](/pictures/frwiki/51/3666579d36d67f61ea6dec78a85ef939.png)
![[L_m, L_n]a = (m - n)L_{m + n}a + \delta_{m + n, 0} \frac{m^3-m}{12}ca\,](/pictures/frwiki/48/0c8b01d5bf82fd40fc89deb26cdf23d5.png)