- Espace topologique normal
-
Espace normal
Un espace topologique séparable X est dit normal lorsque, pour tout couple de fermés disjoints E et F de X, il existe un couple d'ouverts disjoints U et V tels que U contienne E et V, F.
En mathématiques, un espace normal est un cas particulier d'espace topologique. Cette définition est à la base de résultats comme le lemme d'Urysohn ou le théorème de prolongement de Tietze.
Elle provient du mathématicien Heinrich Tietze et date de 1923[1]. Nicolas Bourbaki précise à son sujet : « Les travaux récents ont mis en évidence que, dans ce genre de question (topologie algébrique), la notion d'espace normal est peu maniable, parce qu'elle offre trop de possibilités de pathologie ; on doit le plus souvent lui substituer la notion plus restrictive d'espace paracompact, introduite en 1944 par Jean Dieudonné. »[1]
Sommaire
Définition
Soit X un espace topologique. On dit que X est normal[2] s'il est séparé, et si pour tout couple d'ensembles fermés A et B disjoints, il existe deux ouverts disjoints U et V tels que: A soit inclus dans U et B dans V.
Propriétés
Propriétés élémentaires
-
- Si X et Y sont deux espaces topologiques homéomorphes et si l'un d'eux est normal, l'autre l'est aussi[3].
En effet, on suppose ici que X est normal et que φ est un homéomorphisme entre X et Y. Y est séparé car cette propriété est transférée par homéomorphisme. Soit AY et BY deux fermés disjoints de Y et AX et BX leurs images réciproque par φ. Le fait que φ soit continue montre que AX et BX sont deux fermées disjoints. Il existe deux ouverts U contenant AX et V contenant BX, disjoints car X est normal. Les ensembles φ(U) et φ(V) contiennent respectivement AY et BY par construction et sont disjoints. De plus, ils sont fermés car la réciproque de φ est continue, ce qui termine la démonstration.
-
- Un espace topologique X métrisable est normal[4].
Un espace topologique métrisable est un espace tel qu'il existe une distance dont la topologie induite se confond avec celle de l'espace.
-
- Un espace compact X est normal[5].
La démonstration est un peu analogue à celle qui montre qu'un sous espace compact est fermé.
Détails des démonstrations-
- Un espace topologique X métrisable est normal :
Soit A et B deux fermés disjoints de X. Considérons la fonction f, de X dans [0, 1], définie par :
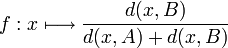
Soit C une partie de X, la notation x → d(x, C) désigne la fonction suivante :
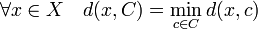
Cette fonction est continue car elle est 1-lipschitzienne. En effet, soit x et y deux éléments de X :
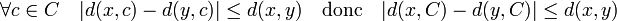
Le dénominateur de la fonction f ne s'annule que pour les points à distance nulle de A et de B. Un point à distance nulle d'un sous-espace est adhérent à cet ensemble. Comme A et B sont fermés, un tel point est à la fois élément de A et de B. Comme ces ensembles sont disjoints, le dénominateur de f ne s'annule jamais. La fonction f est composée de fonction continue, elle est continue. Elle vaut 1 sur A et 0 sur B. En conséquence, les images réciproques des ouverts [0, 1/2[ et ]1/2, 1] de [0, 1] par la fonction f sont deux ouverts disjoints contenant A pour l'un et B pour l'autre. Ce qui termine la démonstration.
Remarque : La fonction f est utilisée pour établir un cas particulier du lemme d'Urysohn.
-
- Un espace compact X est normal :
Les lettres A et B désignent encore deux fermés disjoints de X. Soit a un point de A, montrons tout d'abord qu'il existe un ouvert Ua contenant a et un ouvert Va contenant B d'intersection vide. Soit b un élément de B, il existe deux ouverts Uab contenant a et Vab contenant b d'intersection vide, car X est un espace compact et donc séparé par définition.
Si b décrit B, la famille (Vab) est un recouvrement ouvert de B, comme B est un fermé d'un compact, il est compact et on peut extraire un sous-recouvrement fini (Vabn). On note Va l'union des ouverts du recouvrement fini, par construction c'est un ouvert contenant B. Soit (Uabn) les ouverts contenant a associés et Ua l'intersection de ces ouverts. C'est un ouvert contenant a qui, par construction, est d'intersection vide avec Va.
Si a décrit A, la famille (Ua) est un recouvrement ouvert de A. Une fois encore, on peut en extraire un sous-recouvrement fini (Uan). Soit U l'union des ouverts de ce sous-recouvrement fini. C'est un ouvert contenant A. Soit (Van) les ouverts associées, ils contiennent tous B et leur intersection V est un ouvert contenant B ayant une intersection vide avec A. Ce qui termine la démonstration.
Conditions nécessaires et suffisantes
Il existe de nombreuses caractérisation d'un espace normal. Ces caractérisations sont à l'origine des propriétés donnant de la valeur à la définition :
-
- Un espace topologique séparé X est normal si, et seulement si, pour tout fermé A de X et tout ouvert U contenant A, il existe un ouvert V contenant A tel que l'adhérence de V soit incluse dans U[6] :
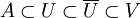
La deuxième condition nécessaire et suffisante, qui découle de la précédente est le lemme d'Urysohn, qui indique qu'un espace séparé est normal si, et seulement si, pour tous fermés disjoints A et B de X, il existe une fonction f continue qui vaut 1 sur A et 0 sur B[7]. L'article détaillé propose une démonstration.
Démonstration- Supposons que X soit normal, les fermés A et cV, où cV désigne le complémentaire de V, sont disjoints donc il existe deux ouverts disjoints U et U1 tels que U contienne A et U1 contienne cV. Le complémentaire cU1 contient U donc contient l'adhérence de U et cette adhérence est incluse dans V, ce qui démontre la première implication.
- Réciproquement, supposons que pour tout fermé A de X et tout ouvert U contenant A, il existe un ouvert V contenant A tel que l'adhérence de V soit incluse dans U. Soit A et B deux fermés disjoints de X, A est inclus dans le complémentaire de B, ce qui montre l'existence d'un ouvert U tel que :
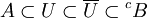
Les ouverts U et le complémentaire de l'adhérence de U vérifient les propriétés demandées.
Annexes
Bibliographie
- (en) M. Henle A combinatorial introduction to topology Dover Publications (1994) (ISBN 0486679667)
- (fr) S. Lang Analyse Réelle InterEditions, Paris (1977) (ISBN 2729600595)
Source externe
Historique
- S. Mehl Tietze Heinrich par le site Chronomath.com
Mathématiques
- F. Paulin Topologie, analyse et calcul différentiel École Normale supérieure (2008-2009)
Références
- ↑ a et b Nicolas Bourbaki Éléments d'histoire des mathématiques Springer-Verlag (éd 2006) p 205 (ISBN 3540339388)
- ↑ S. Lang Analyse Réelle InterEditions, Paris (1977) p 29 (ISBN 2729600595)
- ↑ J. Dugundji Topology Wm. C. Brown Publishers (1989) p 144 (ISBN 0697068897)
- ↑ F. Paulin Topologie, analyse et calcul différentiel École Normale supérieure (2008-2009) p 36
- ↑ S. Lang Analyse Réelle InterEditions, Paris (1977) p 30 (ISBN 2729600595)
- ↑ S. Lang Analyse Réelle InterEditions, Paris (1977) p 36 (ISBN 2729600595)
- ↑ S. Lang Analyse Réelle InterEditions, Paris (1977) p 37 (ISBN 2729600595)
Portail des mathématiques
Catégorie : Topologie générale -
Wikimedia Foundation. 2010.
