Unifère
- Unifère
-
Élément neutre
En mathématiques, un élément neutre (ou élément identité) d'un ensemble pour une loi de composition interne est un élément de cet ensemble qui laisse tous les autres éléments inchangés lorsqu'il est combiné avec eux par cette loi. Un ensemble possédant un élément neutre est dit unifère.
Définition
Soit E un ensemble muni d'une loi de composition interne 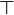 . Soit
. Soit 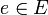 .
.
- e est dit élément neutre à gauche si
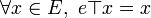 .
.
- e est dit élément neutre à droite si
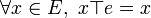 .
.
- e est dit élément neutre s'il est neutre à droite et à gauche.
Exemples
L'élément neutre ne l'est que pour la loi considérée :
- 0 est l'élément neutre de l’addition arithmétique, ainsi que du « ou » binaire.
- 1 est l'élément neutre de la multiplication arithmétique, ainsi que du « et » binaire.
- La matrice unité d'ordre n est l'élément neutre de la multiplication des matrices carrées d'ordre n.
- Le mot vide ε est l'élément neutre de la concaténation des chaînes de caractères.
- Si E = {e1,e2} et est muni de la loi de composition interne
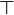 définie par
définie par 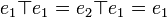 et
et 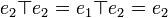 , alors e1 et e2 sont tous les deux éléments neutres à gauche. Il n'y a pas dans ce cas d'élément neutre à droite.
, alors e1 et e2 sont tous les deux éléments neutres à gauche. Il n'y a pas dans ce cas d'élément neutre à droite.
Propriétés
- Il est possible que l'élément neutre à gauche (resp. à droite) ne soit pas unique. Par exemple, considérons un ensemble E contenant au moins deux éléments . on peut définir une loi G sur E par la formule G(x,y) = x et une loi D par la formule D(x,y) = y. Pour la loi G, tout élément est neutre à droite et aucun n'est neutre à gauche. Pour la loi D, tout élément est neutre à gauche et aucun n'est neutre à droite.
- En revanche, s'il existe un élément neutre à gauche et un élément neutre à droite (a priori égaux ou non), alors l'ensemble admet un unique élément neutre, et en outre, tout élément neutre à gauche (resp. à droite) lui est égal. En effet, cette propriété est une conséquence du lemme suivant : soit un ensemble muni d'une loi de composition interne
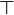 ayant un élément neutre à gauche eg et un élément neutre à droite ed, alors
ayant un élément neutre à gauche eg et un élément neutre à droite ed, alors 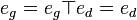 .
.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Algèbre générale | Zéro
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Unifère de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Loi De Composition Interne — L’algèbre est la branche des mathématiques qui s’intéresse aux ensembles et aux relations qui peuvent y être établies. Elle recherche les conséquences générales qui découlent des propriétés de ces relations, indépendamment de la nature précise… … Wikipédia en Français
Relation ternaire interne — Une relation ternaire interne dans un ensemble associe des éléments de cet ensemble à des couples formés d’éléments de ce même ensemble. Sommaire 1 Définitions 2 Exemples 2.1 Propriétés … Wikipédia en Français
Loi de composition interne — Une loi de composition interne (ou, parfois, opération[1]) est un procédé qui, à deux éléments d un ensemble E, associe un troisième élément de E. L addition et la multiplication sont des exemples classiques de lois de composition interne des… … Wikipédia en Français
Algèbre sur un corps — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre sur un corps commutatif K, ou simplement une K algèbre, est une structure algébrique (A , + , . , × ) telle que : (A, +, ·) est un espace vectoriel sur K,… … Wikipédia en Français
Structure algebrique — Structure algébrique En mathématiques, plus particulièrement en algèbre, une structure algébrique est un type particulier de structure. Sa spécificité par rapport aux autres types de structure est d être formée d’un ensemble combiné à une ou… … Wikipédia en Français
Structure algébrique — En mathématiques, plus particulièrement en algèbre, une structure algébrique est un type particulier de structure. Sa spécificité par rapport aux autres types de structure est d être formée d’un ensemble combiné à une ou plusieurs lois de… … Wikipédia en Français
Algèbre associative — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre associative (sur un anneau commutatif A) est un anneau (ou simplement un pseudo anneau) B, muni d une structure supplémentaire de module sur A et tel que la loi… … Wikipédia en Français
Groupe des unités — En mathématiques, et plus particulièrement en algèbre, le groupe des unités est une notion de la théorie des anneaux. Il est constitué de l ensemble des éléments de l anneau ayant un inverse pour la deuxième loi. On l appelle parfois groupe des… … Wikipédia en Français
Anneau Commutatif — Dans la théorie des anneaux, un anneau commutatif est un anneau dans lequel la loi de multiplication est commutative. Cela signifie que pour tous les éléments a et b de l’anneau, on a a*b=b*a, en notant * cette loi de multiplication. L’étude des… … Wikipédia en Français
Anneau abélien — Anneau commutatif Dans la théorie des anneaux, un anneau commutatif est un anneau dans lequel la loi de multiplication est commutative. Cela signifie que pour tous les éléments a et b de l’anneau, on a a*b=b*a, en notant * cette loi de… … Wikipédia en Français
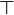 . Soit
. Soit 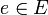 .
.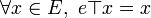 .
.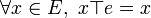 .
.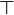 définie par
définie par 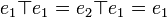 et
et 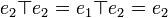 , alors e1 et e2 sont tous les deux éléments neutres à gauche. Il n'y a pas dans ce cas d'élément neutre à droite.
, alors e1 et e2 sont tous les deux éléments neutres à gauche. Il n'y a pas dans ce cas d'élément neutre à droite.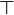 ayant un élément neutre à gauche eg et un élément neutre à droite ed, alors
ayant un élément neutre à gauche eg et un élément neutre à droite ed, alors 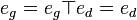 .
.