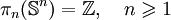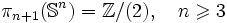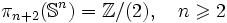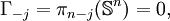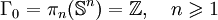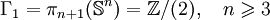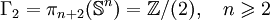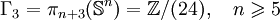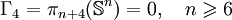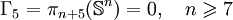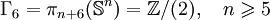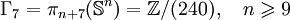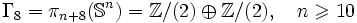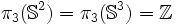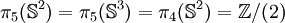Groupes D'homotopie Des Sphères

Groupes d'homotopie des sphères

En mathématiques, et plus spécifiquement en topologie algébrique, les groupes d'homotopie des sphères sont des invariants qui décrivent, en termes algébriques, comment des sphères de dimensions égales ou différentes peuvent s'enrouler l'une sur l'autre.

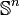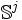Le groupe d'homotopie d'ordre j de la sphère de dimension n, $\mathbb{S}^n$ , est l'ensemble, noté $\pi_{j}(\mathbb{S}^n) =[\mathbb{S}^j\to\mathbb{S}^n]$ , des classes d'homotopie d'applications qui envoient un point fixé de la sphère $\mathbb{S}^j$ sur un point fixé de la sphère 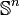$\mathbb{S}^n$ . Cet ensemble (pour j et n fixés), noté 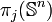$\pi_{j}(\mathbb{S}^n)$ , peut être muni d'une structure de groupe abélien.

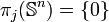Si j < n, ce groupe est réduit à un seul élément : $\pi_{j}(\mathbb{S}^n)=\{0\}$ .

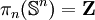Si j = n, ce groupe est monogène infini (c'est-à-dire infini et engendré par un seul élément) : $\pi_{n}(\mathbb{S}^n)=\mathbf{Z}$ .

Si j > n, le groupe 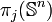$\pi_{j}(\mathbb{S}^n)$ est soit un groupe fini, soit la somme d'un groupe fini et d'un groupe infini monogène.

La suite spectrale de Serre fut inventée pour calculer les groupes d'homotopie des sphères, mais aucune liste complète de ces groupes n'est connue. Pour calculer ces groupes, on utilise aussi les fibrations de Hopf et la technique des variétés équipées (framed en anglais) qui provient de la théorie du cobordisme.

Propriétés générales

Nous donnons quelques résultats :

Les groupes d'homotopie des sphères sont des groupes abéliens de type fini (avec un nombre fini de générateurs).
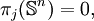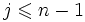
$\pi_j(\mathbb{S}^n)=0,\quad$ pour $\quad j\leqslant n-1$
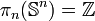
$\pi_n(\mathbb{S}^n)=\mathbb{Z}$

Dimension 1

En dimension 1, on a:

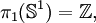
$\pi_1(\mathbb{S}^1)=\mathbb{Z},$
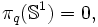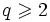
$\pi_q(\mathbb{S}^1)=0,\quad$ pour $\quad q\geqslant 2$

Dimensions 2 et 3

En dimension 2 et 3, la fibration de Hopf et d'autres techniques permettent d'obtenir :

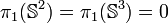
$\pi_1(\mathbb{S}^2)=\pi_1(\mathbb{S}^3)=0$
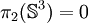
$\pi_2(\mathbb{S}^3)=0$
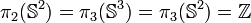
$\pi_2(\mathbb{S}^2)=\pi_3(\mathbb{S}^3)=\pi_3(\mathbb{S}^2)=\mathbb{Z}$
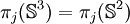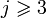
$\pi_j(\mathbb{S}^3)=\pi_j(\mathbb{S}^2)$ pour $j\geqslant 3$
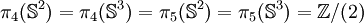
$\pi_4(\mathbb{S}^2)=\pi_4(\mathbb{S}^3)=\pi_5(\mathbb{S}^2)=\pi_5(\mathbb{S}^3)=\mathbb{Z}/(2)$
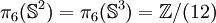
$\pi_6(\mathbb{S}^2)=\pi_6(\mathbb{S}^3)=\mathbb{Z}/(12)$

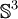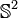
**Groupes d'homotopie de $\mathbb{S}^3$ et $\mathbb{S}^2$**
$k$	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22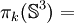
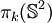
$\pi_k(\mathbb{S}^3)=$ $\pi_k(\mathbb{S}^2)$	Z	Z₂	Z₂	Z₁₂	Z₂	Z₂	Z₃	Z₁₅	Z₂	Z₂²	Z₁₂⊕Z₂	Z₈₄⊕Z₂²	Z₂²	Z₆= Z₂⊕Z₃	Z₃₀= Z₂⊕Z₁₅	Z₃₀= Z₂⊕Z₁₅	Z₂⊕Z₆= Z₂²⊕Z₃	Z₂²⊕Z₁₂	Z₂²⊕Z₁₂	Z₂²⊕Z₁₃₂

Théorie générale

Calculer les groupes d'homotopie des sphères est difficile et les résultats sont compliqués. La table suivante donne une idée de la complexité :

	π₁	π₂	π₃	π₄	π₅	π₆	π₇	π₈	π₉	π₁₀	π₁₁	π₁₂	π₁₃	π₁₄	π₁₅
S¹	Z	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S²	0	Z	Z	Z₂	Z₂	Z₁₂	Z₂	Z₂	Z₃	Z₁₅	Z₂	Z₂²	Z₁₂×Z₂	Z₈₄×Z₂²	Z₂²
S³	0	0	Z	Z₂	Z₂	Z₁₂	Z₂	Z₂	Z₃	Z₁₅	Z₂	Z₂²	Z₁₂×Z₂	Z₈₄×Z₂²	Z₂²
S⁴	0	0	0	Z	Z₂	Z₂	Z×Z₁₂	Z₂²	Z₂²	Z₂₄×Z₃	Z₁₅	Z₂	Z₂³	Z₁₂₀×Z₁₂×Z₂	Z₈₄×Z₂⁵
S⁵	0	0	0	0	Z	Z₂	Z₂	Z₂₄	Z₂	Z₂	Z₂	Z₃₀	Z₂	Z₂³	Z₇₂×Z₂
S⁶	0	0	0	0	0	Z	Z₂	Z₂	Z₂₄	0	Z	Z₂	Z₆₀	Z₂₄×Z₂	Z₂³
S⁷	0	0	0	0	0	0	Z	Z₂	Z₂	Z₂₄	0	0	Z₂	Z₁₂₀	Z₂³
S⁸	0	0	0	0	0	0	0	Z	Z₂	Z₂	Z₂₄	0	0	Z₂	Z×Z₁₂₀
S⁹	0	0	0	0	0	0	0	0	Z	Z₂	Z₂	Z₂₄	0	0	Z₂

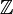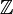Les entrées de la table sont soit le groupe trivial 0, soir le groupe monogène infini $\mathbb Z$ , soit les groupes abéliens finis ou encore (cases rouges) le produit de tels groupes finis abéliens et de $\mathbb Z$ .

Stabilité en grandes dimensions

Pour les dimensions supérieures, on a:

$\pi_{n}(\mathbb{S}^{n})=\mathbb{Z},\quad n\geqslant 1$
$\pi_{n+1}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 3$
$\pi_{n+2}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 2$

Comme il peut être conjecturé, il s'avère que 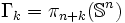$\Gamma_k=\pi_{n+k}(\mathbb{S}^{n})$ est indépendant de $n$ pour $n$ suffisamment grand. Ce phénomène est connu sous le nom de stabilité. Il résulte du théorème de Freudenthal suivant :

Le morphisme de suspension 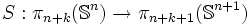$S:\pi_{n+k}(\mathbb{S}^n)\to\pi_{n+k+1}(\mathbb{S}^{n+1})$ est un isomorphisme pour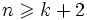 $n\geqslant k+2$
et un épimorphisme (morphisme surjectif) pour $n = k + 1$ .

Liste des groupes d'homotopie stable

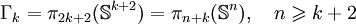
Nous donnons la liste des premiers groupes stables $\Gamma_k=\pi_{2k+2}(\mathbb{S}^{k+2})=\pi_{n+k}(\mathbb{S}^{n}),\quad n\geqslant k+2$

$\Gamma_{-j}=\pi_{n-j}(\mathbb{S}^{n})=0,$
$\Gamma_0=\pi_{n}(\mathbb{S}^{n})=\mathbb{Z},\quad n\geqslant 1$
$\Gamma_1=\pi_{n+1}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 3$
$\Gamma_2=\pi_{n+2}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 2$
$\Gamma_3=\pi_{n+3}(\mathbb{S}^{n})=\mathbb{Z}/(24),\quad n\geqslant 5$
$\Gamma_4=\pi_{n+4}(\mathbb{S}^{n})=0,\quad n\geqslant 6$
$\Gamma_5=\pi_{n+5}(\mathbb{S}^{n})=0,\quad n\geqslant 7$
$\Gamma_6=\pi_{n+6}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 5$
$\Gamma_7=\pi_{n+7}(\mathbb{S}^{n})=\mathbb{Z}/(240),\quad n\geqslant 9$
$\Gamma_8=\pi_{n+8}(\mathbb{S}^{n})=\mathbb{Z}/(2)\oplus\mathbb{Z}/(2),\quad n\geqslant 10$

Les groupes d'homotopie stable sont finis sauf pour $k = 0$ .

**Groupes d'homotopie stable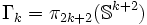** $\ \Gamma_k=\pi_{2k+2}(\mathbb{S}^{k+2})$
$k$	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
$Γ k$	Z	Z₂	Z₂	Z₂₄= Z₈ ⊕Z₃	0	0	Z₂	Z₂₄₀= Z₁₆⊕Z₃ ⊕Z₅	Z₂²	Z₂³	Z₆	Z₅₀₄= Z₈⊕Z₉ ⊕Z₇	0	Z₃	Z₂²	Z₄₈₀⊕Z₂= Z₃₂⊕Z₂ ⊕Z₃⊕Z₅	Z₂²	Z₂⁴	Z₈⊕Z₂	Z₂₆₄⊕Z₂= Z₈⊕Z₂ ⊕Z₃⊕Z₁₁	Z₂₄	Z₂²	Z₂²	Z₁₆⊕Z₈⊕Z₂ ⊕Z₉⊕Z₃ ⊕Z₅⊕Z₇⊕Z₁₃

p-composantes des groupes d'homotopie stable

Voir l'article Groupe abélien de type fini pour la classification des groupes abéliens finis et la notion de p-composante.

La table précédente incite à s'intéresser à la classe de congruence modulo 4 de k, si p est un nombre premier supérieur à 5 :

Si k est divisible par 4 ou congru à 1 ou 2 modulo 4, la p-composante de $Γ k$ est 0 (quel que soit p > 5 premier).
Si k est congru à 3 (ou -1) modulo 4, la p-composante de $Γ k$ est cyclique et d'ordre p ( 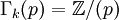$\Gamma_k(p)=\mathbb{Z}/(p)$ ) si (p-1)/2 divise (k+1)/4, sinon elle est nulle (0).

Par exemple 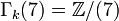$\Gamma_k(7)=\mathbb{Z}/(7)$ si $k = 12 n - 1$ et $Γ k (7) = 0$ sinon.

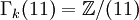$\Gamma_k(11)=\mathbb{Z}/(11)$ si $k = 20 n - 1$ et $Γ k (11) = 0$ sinon.

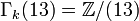$\Gamma_k(13)=\mathbb{Z}/(13)$ si $k = 24 n - 1$ et $Γ k (13) = 0$ sinon.

La complexité réside essentiellement dans les 2-, 3- et 5- composantes du groupe $Γ k$ .

Groupes d'homotopie non stables

Les premiers groupes non stables sont les suivants :

Pour
- $\pi_3(\mathbb{S}^2)=\pi_3(\mathbb{S}^3)=\mathbb{Z}$
- $\pi_5(\mathbb{S}^2)=\pi_5(\mathbb{S}^3)=\pi_4(\mathbb{S}^2)=\mathbb{Z}/(2)$
- $\pi_6(\mathbb{S}^2)=\pi_6(\mathbb{S}^3)=\mathbb{Z}/(12)$
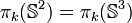
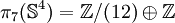
$\pi_7(\mathbb{S}^4)=\mathbb{Z}/(12)\oplus\mathbb{Z}$

Groupes d'homotopie infinis

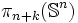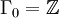Les groupes d'homotopie stable $\pi_{n+k}(\mathbb{S}^{n})$ sont finis sauf pour $k = 0$ ( $\Gamma_0=\mathbb{Z}$ ).

Les groupes d'homotopie instables sont finis sauf les groupes 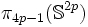$\pi_{4p-1}(\mathbb{S}^{2p})$ . Ces derniers ( 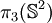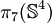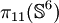$\pi_{3}(\mathbb{S}^{2})$ , $\pi_{7}(\mathbb{S}^{4})$ , $\pi_{11}(\mathbb{S}^{6})$ , ...) sont isomorphes à la somme directe de $\mathbb{Z}$ et d'un groupe fini.

Groupes d'homotopie non nuls

On sait que si n>1 il y a une infinité de groupes 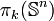$\pi_{k}(\mathbb{S}^{n})$ qui sont non nuls (ce sont des résultats de Jean-Pierre Serre).

On sait aussi que 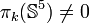$\pi_k(\mathbb{S}^{5})\neq 0$ pour tout k>4 (M.L. Curtis).

Applications

Pour les applications du groupe fondamental (n=1), voir l'article Groupe fondamental.
Le fait que 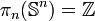$\pi_{n}(\mathbb{S}^{n})=\mathbb{Z}$ implique le théorème de Brouwer qui affirme que toute application continue de la boule (de dimension >1) dans elle-même a un point fixe.

Ce groupe permet de définir le degré de Brouwer d'une application de la sphère dans elle-même.

Les groupes d'homotopie stable sont importants en théorie des singularités.
Le fait que le 3^e groupe d'homotopie stable est 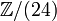$\mathbb{Z}/(24)$ implique le théorème de Rokhlin qui affirme que la signature d'une variété spinorielle de dimension 4 est divisible par 16.
Les groupes d'homotopie stable servent à décrire les groupes de h-cobordisme des homotopies orientées de sphères, qui pour 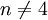$n\neq 4$ est le groupe des sphères exotiques orientées de dimension n.
Les groupes d'homotopie des sphères sont liés aux classes de bordisme des variétés.
Ils permettent également de calculer les groupes d'homotopie des fibrés, des groupes de Lie et des espaces symétriques.

Généralisation en géométrie algébrique

En géométrie algébrique, on définit les 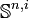$\mathbb{S}^{n,i}$ qui sont les sphères de dimension n et de poids i.

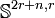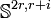
On peut définir les groupes d'homotopie stable des sphères comme colimites (ou limite inductive) de l'ensemble des classes d'homotopie d'applications de $\mathbb{S}^{2r+n,r}$ vers $\mathbb{S}^{2r,r+i}$

Références en français

Doubrovine, Novikov, Fomenko : Géométrie contemporaine : tomes 2 et 3 , ed. Mir.
Claude Godbillon : Eléments de Topologie algébrique, ed. Hermann.
Fabien Morel : Groupes d'homotopie de sphères algébriques et formes quadratiques in Leçons de mathématiques d'aujourd'hui, volume 3, ed. Cassini (2007)

Ce document provient de « Groupes d%27homotopie des sph%C3%A8res ».

Catégories : Invariant | Groupe remarquable | Topologie algébrique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupes D'homotopie Des Sphères de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Groupes d'homotopie des spheres — Groupes d homotopie des sphères En mathématiques, et plus spécifiquement en topologie algébrique, les groupes d homotopie des sphères sont des invariants qui décrivent, en termes algébriques, comment des sphères de dimensions égales ou… … Wikipédia en Français
Groupes d'homotopie des sphères — Enroulement d une sphère à deux dimensions autour d une autre sphère En mathématiques, et plus spécifiquement en topologie algébrique, les groupes d homotopie des sphères sont des invariants qui décrivent, en termes algébriques, comment des… … Wikipédia en Français
Groupes d'homotopie — Groupe d homotopie En mathématiques, et plus particulièrement en topologie et topologie algébrique, les groupes d homotopie sont des invariants qui généralisent la notion de groupe fondamental aux dimensions supérieures. Sommaire 1 Définition… … Wikipédia en Français
Groupe d'homotopie — En mathématiques, et plus particulièrement en topologie et topologie algébrique, les groupes d homotopie sont des invariants qui généralisent la notion de groupe fondamental aux dimensions supérieures. Sommaire 1 Définition mathématique 2 Produit … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
GROUPES (mathématiques) - Groupes de Lie — La théorie des groupes de Lie, fondée dans la période de 1870 1880 par le mathématicien norvégien Sophus Lie, a d’abord été considérée comme une partie assez marginale des mathématiques, liée à des problèmes touchant les équations différentielles … Encyclopédie Universelle
Homotopy groups of spheres — In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure… … Wikipedia
Géométrie différentielle des surfaces — En mathématiques, la géométrie différentielle des surfaces est la branche de la géométrie différentielle qui traite des surfaces (les objets géométriques de l espace usuel E3, ou leur généralisation que sont les variétés de dimension 2), munies… … Wikipédia en Français
Catégorie des variétés différentielles — Variété (géométrie) Pour les articles homonymes, voir Variété. Réalisation du ruban de Möbius, à partir du collage d une bande de papier. Le bord n est que d … Wikipédia en Français
TOPOLOGIE - Topologie algébrique — Inventée au début du XXe siècle pour résoudre des problèmes géométriques, la topologie algébrique connut un grand développement grâce à l’introduction de constructions algébriques de plus en plus abstraites. Pour clarifier l’exposé, on a… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Groupes D'homotopie Des Sphères