Graphe Petersen

Graphe de Petersen
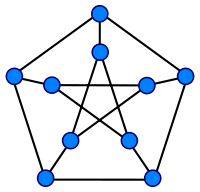
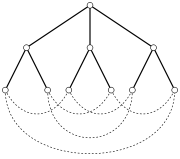
Schéma classique du graphe de Petersen, sous la forme d'un pentagone et d'un pentagramme concentriques, reliés par cinq rayons.
Nombre de sommets	10
Nombre d'arêtes	15
Distribution des degrés	3-régulier
Diamètre	2
Propriétés	Hypohamiltonien, non-planaire, cubique

Le graphe de Petersen est, en théorie des graphes, un graphe possédant 10 sommets et 15 arêtes.

Il s'agit d'un petit graphe qui sert d'exemple et de contre-exemple pour plusieurs problèmes de la théorie des graphes. Il porte le nom de Julius Petersen qui le construisit en 1898 en tant que plus petit graphe cubique sans isthme dont les arêtes ne peuvent être coloriées avec trois couleurs^[1]. Il a cependant été mentionné pour la première fois 12 ans auparavant, en 1886^[2].

Sommaire 1 Constructions 2 Propriétés 2.1 Plongements 2.2 Symétries 3 Chemins et cycles hamiltoniens 3.1 Coloration 3.2 Autres propriétés 4 Voir aussi 4.1 Liens internes 4.2 Liens externes 4.3 Références

Constructions

Le graphe de Petersen est le complément du graphe ligne de K₅. C'est également le graph de Kneser KG_5,2; il est donc possible de construire le graphe de Petersen en considérant un sommet pour chaque couple d'un ensemble de 5 éléments, et en connectant deux sommets si les couples correspondants sont disjoints.

Géométriquement, le graphe de Petersen est le graphe formé par les sommets et les arêtes de l'hémi-dodécaèdre, un dodécaèdre dont les sommets, arêtes et faces opposés sont identifiés deux à deux.

Propriétés

Plongements

Le graphe de Petersen n'est pas planaire. Tout graphe non-planaire possède comme mineur soit le graphe complet K₅, soit le graphe bipartite complet K_3,3 ; le graphe de Petersen possède les deux.

Le dessin plan le plus courant schématise le graphe de Petersen sous la forme d'un pentagramme inclus dans un pentagon, et possède cinq croisements. Ce dessin ne minimise pas les croisements ; il est possible de représenter le graphe de Petersen avec seulement deux croisements. Sur un tore, le graphe de Petersen peut être représenté sans croisement ; son genre est donc égal à 1.

Il est possible de dessiner le graphe de Petersen dans le plan (avec croisements) de telle façon que toutes les arêtes ont la même longueur.

La plus simple surface non-orientable sur laquelle le graphe de Petersen peut être plongé sans croisement est le plan projectif. Ce plongement est donné par la construction à partir de l'hémi-dodécaèdre.

Symétries

Le graphe de Petersen est fortement régulier. Il est également symétrique, c'est est dire qu'il est sommet-transitif et arête-transitif.

L'groupe d'automorphisme du graphe de Petersen est le groupe symétrique S₅ ; l'action de S₅ sur le graphe de Petersen découle de sa construction comme graphe de Kneser. Tout homomorphisme du graphe de Petersen sur lui-même qui n'identifie pas des sommets adjacents est un automorphisme. Les représentations planaires du graphe de Petersen ne peuvent pas représenter la totalité de son groupe symétrique.

Malgre son degré de symétrie élevé, le graphe de Petersen n'est pas un graphe de Cayley, le plus petit graphe sommet-transitif à ne pas l'être.

Chemins et cycles hamiltoniens

Le graphe de Petersen possède un chemin hamiltonien mais aucun cycle hamiltonien, le plus petit graphe cubique sans isthme dans ce cas. Il est hypohamiltonien, c'est à dire que la suppression de n'importe quel sommet du graphe de Petersen suffit à le rendre hamiltonien ; il s'agit du plus petit graphe hypohamiltonien. Le graphe de Petersen est l'un des cinq graphes sommet-transitifs connexes sans cycle hamiltonien connus.

Coloration

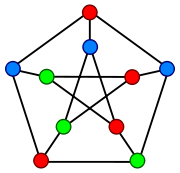
Le graphe de Petersen possède un nombre chromatique de 3 : ses sommets peuvent être coloriés à l'aide de trois couleurs, mais pas avec deux, de telle façon qu'aucune arêtes ne connecte deux sommets de la même couleur.

Son index chromatique est égal à 4 : colorier ses arêtes nécessite 4 couleurs. Le graphe de Petersen est donc un snark. Il s'agit du plus petit snark possible.

Le graphe possède un index chromatique fractionel de 3, montrant que la différence entre l'index chromatique et l'index chromatique fractionnel d'un graphe peut être égale à 1. La conjecture de Goldberg-Seymour suppose qu'il s'agit de la plus grande différence possible.

Le nombre de Thue (une variant de l'index chromatique) du graphe de Petersen est égale à 5.

Autres propriétés

Le graphe de Petersen :

• est 3-connexe et donc 3-arête-connexe et sans isthme ;
• est tripartite ;
• est cubique ;
• possède un rayon et un diamètre égaux à 2 (le plus grand graphe cubique de diamètre 2) ;
• possède comme spectre de graphe -2, -2, -2, -2, 1, 1, 1, 1, 1, 3 ;
• est le plus petit graphe cubique de maille 5 ;
• est la seule (3,5)-cage ;
• est un graphe de Moore ;
• possède 2 000 arbre d'expansion, le maximum parmi les graphes cubiques à 10 sommets ;
• est distance-unité.

Voir aussi

Liens internes

• Théorie des graphes

Liens externes

• (en) Petersen Graph (Mathworld)

Références