Graphe De Coxeter

Graphe De Coxeter

Graphe de Coxeter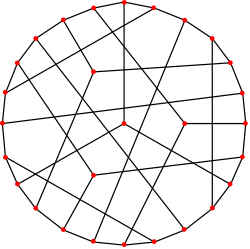

Graphe de Coxeter
Coxeter graph.svg
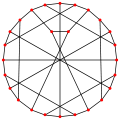
Le graphe de Coxeter
Nombre de sommets 28
Nombre d'arêtes 42
Distribution des degrés 3-régulier
Diamètre 4
Propriétés Hypohamiltonien, cubique, symétrique


En théorie des graphes, le graphe de Coxeter est un graphe cubique symétrique à 28 sommets et 42 arêtes[1]. Il est nommé en l'honneur de H.S.M. Coxeter qui l'appelait "My graph"[2]. Dans le Foster Census classifiant tout les graphes cubiques symétriques il est numéroté F028A[3].

Le graphe Coxeter a une maille de 7 et un diamètre de 4[4]. Il a pour groupe d'automorphisme le groupe projectif linéaire PGL(2,7) d'ordre 336. Son nombre chromatique est égal à 3.

Le graphe de Coxeter n'est pas planaire. En fait pour le dessiner sur un plan il faut nécessairement que plusieurs arêtes se croisent. Il est possible de le dessiner avec seulement 11 croisements, mais le fait que ce nombre soit minimal est une conjecture[5]. Une autre conjecture énoncée par Pegg et Exoo en 2009 expose que le graphe de Coxeter, avec ses 28 sommets, serait le plus petit graphe cubique nécessitant 11 croisements pour être dessiné sur le plan[6].

Chemins et cycles hamiltoniens

Le graphe de Coxeter est remarquable car il est à la fois sommet-transitif et non-hamiltonien. C'est, avec K2 et le graphe de Petersen, un des cinq graphes sommet-transitif connexe sans cycle hamiltonien connu. La conjecture de Lovász stipule que tous les graphes sommet-transitifs sont hamiltoniens sauf ces cinq là.

Bien que le graphe de Coxeter ne possède pas de cycle hamiltonien, il possède un chemin hamiltonien. J. A. Bondy prouva en 1972 qu'il est hypohamiltonien, c'est à dire que la suppression de n'importe quel sommet du graphe de Coxeter suffit à le rendre hamiltonien[7].

Galerie

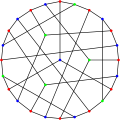
Le graphe obtenu depuis le graphe de Coxeter par excision d'une arête

Le graphe de Coxeter admet une 3-coloration

Le graphe de Coxeter peut être dessiné sur le plan avec 11 croisements d'arêtes

Notes et références

  1. ↑ Brouwer, A. E. Coxeter Graph
  2. ↑ (en) H.S.M. Coxeter, My graph, Proc. London Math. Soc. 46 (1983) 117-136.
  3. ↑ (en) Gordon Royle , Marston Conder , Brendan McKay and Peter Dobscanyi, Cubic symmetric graphs (The Foster Census)
  4. ↑ Gordon Royle F028A
  5. ↑ (en) Rectilinear Drawings of Famous Graphs on Geoffrey Exoo hompage
  6. ↑ (en) Pegg, E. T. and Exoo, G. "Crossing Number Graphs." Mathematica J. 11, 2009
  7. ↑ Bondy, J. A. "Variations of the Hamiltonian Theme." Canad. Math. Bull. 15, 57-62, 1972.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Graphe de Coxeter ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Graphe De Coxeter de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Graphe de Coxeter — Représentation du graphe de Coxeter. Nombre de sommets 28 Nombre d arêtes 42 Distribution des degrés 3 régulier Rayon 4 …   Wikipédia en Français

  • Graphe de coxeter — Le graphe de Coxeter Nombre de sommets 28 Nombre d arêtes 42 Distribution des degrés 3 régulier Diamètre 4 Propriétés Hypohamilton …   Wikipédia en Français

  • Graphe de Petersen — Schéma classique du graphe de Petersen, sous la forme d un pentagone et d un pentagramme concentriques, reliés par cinq rayons. Nombre de sommets 10 Nombre d arêtes 15 Distribution des degrés 3 régulier …   Wikipédia en Français

  • Graphe distance-régulier — En théorie des graphes, un graphe est distance régulier si pour tous sommets , le nombre de sommets voisins de u à distance i et le nombre de sommets voisins de v à distance j ne dépendent que de i,j et de la distance d(u,v) entre u et v.… …   Wikipédia en Français

  • Graphe hypohamiltonien — En théorie des graphes, un graphe est hypohamiltonien s il n a pas de cycle hamiltonien mais que la suppression de n importe quel sommet du graphe suffit à le rendre hamiltonien. Sommaire 1 Histoire 2 Planarité 3 Exemples …   Wikipédia en Français

  • Coxeter — H.S.M. Coxeter Harold Coxeter, 1970 Harold Scott MacDonald «Donald» Coxeter (9 février 1907, Londres 31 mars 2003, Toronto, Canada) est un mathématicien britannique …   Wikipédia en Français

  • Graphe de Tutte–Coxeter — Représentation hamiltonienne du graphe de Tutte–Coxeter. Nombre de sommets 30 Nombre d arêtes 45 Distribution des degrés 3 régulier Rayo …   Wikipédia en Français

  • Graphe de Nauru — Représentation du graphe de Nauru. Notation F24A Nombre de sommets 24 Nombre d arêtes 36 Distribution des degrés 3 régulier …   Wikipédia en Français

  • Graphe de Clebsch — Représentation du graphe de Clebsch Nombre de sommets 16 Nombre d arêtes 40 Distribution des degrés 5 régulier Rayon …   Wikipédia en Français

  • Graphe de Moore — En théorie des graphes, un graphe de Moore est un graphe régulier dont le nombre de sommets, pour un degré et un diamètre donnés, est maximal. Les graphes de Moore ont été nommés par Alan Hoffman et Robert Singleton en 1960 en hommage à Edward F …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”