Coloration des aretes d'un graphe

Coloration des arêtes du 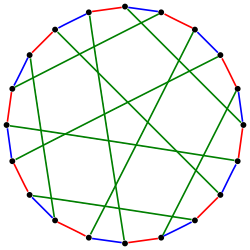graphe de Desargues avec trois couleurs.

La coloration des arêtes d’un graphe entre dans la catégorie plus générale des problèmes de coloration de graphes, le but étant d’attribuer une couleur à chaque arête du graphe avec pour principe que deux arêtes ayant un sommet commun n’aient jamais la même couleur, le tout en utilisant le moins de couleurs possibles. La figure ci-contre est un exemple de coloration d’arêtes correcte. On vérifie en effet que chaque sommet ne possède jamais deux arêtes de la même couleur. On remarquera qu’ici, il n’aurait pas été possible d’effectuer la coloration des arêtes du graphe avec moins de trois couleurs différentes.

Définition

Mentionnée sans précision supplémentaire, l’expression « coloration des arêtes d’un graphe » désigne le fait d’attribuer à chaque arête une couleur, de sorte que deux arêtes adjacentes n’aient jamais la même couleur. Ici, deux arêtes adjacentes sont deux arêtes ayant un sommet en commun.

Le nombre minimal de couleurs différentes pouvant être utilisées pour réaliser la coloration des arêtes d’un graphe G est appelé « indice chromatique du graphe » ou « nombre chromatique des arêtes du graphe» : χ′(G), parfois noté χ₁(''G'').

Propriétés

Quelques propriétés de χ′(G):

1. χ′(G) = 1 si et seulement si G est un appariement.
2. χ′(G) ≥ Δ(G).
3. χ′(G) ≤ Δ(G) + 1. (Théorème de Vizing)
4. χ′(G) ≤ Δ(G) + μ(G), où G peut être un multigraphe.
5. χ′(G) = Δ(G) si G est un graphe biparti. (Théorème de König sur les graphes bipartis)
6. χ′(G) = Δ(G) si G est simple, planaire et si Δ(G) ≥ 7. (Vizing en 1965 puis Sanders et Zhao en 2001)

Ici, Δ(G) est le degré maximum de G ; et μ(G), sa multiplicité.

Classification des graphes et détermination de leur nombre chromatique

Comme nous l’avons vu plus haut, χ′(G) = Δ(G) ou χ′(G) = Δ(G) + 1. Quand χ′(G) = Δ(G), on dira que G est de « Classe 1 » ; dans le cas contraire, il sera de « Classe 2 ». En 1981, Holyver a prouvé que la détermination de l’appartenance d’un graphe simple à l’une ou l’autre de ces deux classes est un problème NP-complet. Cependant, pour certains cas particuliers, il existe des règles permettant de conclure rapidement. Par exemple, Vizing, en 1965, a établi qu’un graphe simple et planaire est de Classe 1 si son degré maximal est supérieur ou égal à 8. En revanche, il fit remarquer qu’il existait des graphes simples, planaires et de Classe 2 pour lesquels le degré maximal était de 2, 3, 4 ou 5. Des études supplémentaires l’ont amené à formuler la conjecture suivante :

Conjecture de Vizing pour les graphes planaires : Tout graphe simple, planaire, et de degré maximal égal à 6 ou 7, est de Classe 1.

En 2001, Sanders et Zhao ont partiellement démontré cette conjecture. Ils montrèrent que tout graphe simple, planaire et de degré maximal 7, est de Classe 1. Ainsi, il ne reste plus que le cas des graphes simples, planaires et de degré maximal égal à 6.

Cette conjecture trouve une application dans la conjecture de la coloration totale.

Bibliographie

• Holyer, Ian (1981). The NP-completeness of edge-coloring. SIAM J. Comput. 10, 718–720.
• Jensen, Tommy R.; Toft, Bjarne (1995). Graph coloring problems. New York: Wiley-Interscience. ISBN 0-471-02865-7.
• Kőnig, D. (1916). Über Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre. Mathematische Annalen 77, 453–465.
• Sanders, Daniel P.; Zhao, Yue (2001). Planar Graphs of Maximum Degree Seven are Class I. Journal of Combinatorial Theory, Series B. 83, Issue 2, 201–212.
• Vizing, V. G. (1964). On an estimate of the chromatic class of a p-graph. Diskret. Analiz. 3, 25–30.
• Vizing, V. G. (1965). Critical graphs with given chromatic class (in Russian). Metody Diskret. Analiz. 5, 9–17.