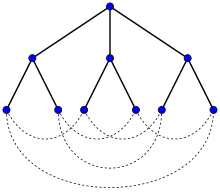
Graphe de Moore

Graphe de Moore

En théorie des graphes, un graphe de Moore est un graphe régulier dont le nombre de sommets, pour un degré et un diamètre donnés, est maximal.

Les graphes de Moore ont été nommés par Alan Hoffman et Robert Singleton en 1960 en hommage à Edward F. Moore, qui avait tenté de décrire et classifier ces graphes.

Sommaire

Définition

Un graphe de Moore est un graphe régulier de degré d et de diamètre k qui possède un nombre de sommets égal à la borne supérieure :

1+d\sum_{i=0}^{k-1}(d-1)^i

De façon générale, le nombre de sommets d'un graphe de degré maximal d et de diamètre k est inférieur ou égal à cette valeur. Un graphe de Moore possède donc une valeur maximale de sommets pour un degré et un diamètre donnés.

De façon alternative, un graphe de Moore est un graphe régulier de diamètre k et de maille 2k+1. Cette définition est équivalente à la précédente.

Il est possible de généraliser la définition pour permettre à un graphe de Moore d'être de maille paire. Dans ce cas, un graphe de Moore est un graphe régulier de degré d>2 et de maille m dont le nombre de sommets est égal à :

1+{d-1}^{\frac {m}{2}-1}+m\sum_{i=0}^{\frac{m-4}{2}}(d-1)^i si m est pair, et
1+d\sum_{i=0}^{\frac{m-3}{2}}(d-1)^i si m est impair.

Exemples

Le graphe de Petersen est un graphe de Moore.

Les graphes complets (de diamètre 1) sont des graphes de Moore. Parmi ceux-ci, les cycles impairs sont des graphes de Moore de degré 2. Les cliques sont des graphes de Moore de diamètre 1.

Le théorème d'Hoffman-Singleton[1] stipule que tout graphe de Moore de maille 5 (et donc de diamètre 2) ne peut avoir qu'un degré 2, 3, 7 ou 57. Il s'agit du pentagone (degré 2 et 5 sommets), du graphe de Petersen (degré 3 et 10 sommets) et du graphe de Hoffman-Singleton (degré 7 et 50 sommets). L'existence d'un graphe de Moore de maille 5 et de degré 57 n'est pas connue; un tel graphe aurait 3 250 sommets.

Si la définition généralisée des graphes de Moore est prise en considération, ils incluent le graphe biparti complet de Kn,n de maille 4, le graphe de Heawood de degré 3 et de maille 6 et le graphe de Tutte–Coxeter de degré 3 et de maille 8. De façon générale, à part les graphes cités ci-dessus, tous les graphes de Moore sont de maille 5, 6, 8 ou 12[2],[3].

Voir aussi

Liens internes

Liens externes

Références

  1. ↑ (en) [PDF] A. J. Hoffman, R. R. Singleton, Moore graphs with diameter 2 and 3, IBM Journal of Research and Development vol. 5, n°4, pp. 497–504, 1960
  2. ↑ (en) E. Bannai, T. Ito, [ http://hdl.handle.net/2261/6123 On Moore graphs], Journal of the Faculty of Sciences, Université de Tokyo Sect. 1 A vol. 20, pp. 191-208 (1973)
  3. ↑ (en) R. M. Damerell, On Moore Graphs, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 74, pp. 227-236 (1973)

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Graphe de Moore de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Graphe de Hoffman-Singleton — Schéma du graphe de Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés …   Wikipédia en Français

  • Graphe de Petersen — Schéma classique du graphe de Petersen, sous la forme d un pentagone et d un pentagramme concentriques, reliés par cinq rayons. Nombre de sommets 10 Nombre d arêtes 15 Distribution des degrés 3 régulier …   Wikipédia en Français

  • Graphe de Heawood — Représentation du graphe de Heawood. Nombre de sommets 14 Nombre d arêtes 21 Distribution des degrés 3 régulier Rayon 3 …   Wikipédia en Français

  • Graphe D'Hoffman-Singleton — Schéma du graphe d Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés 7 régulier Diamètre 2 …   Wikipédia en Français

  • Graphe d'Hoffman-Singleton — Schéma du graphe d Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés 7 régulier Diamètre 2 …   Wikipédia en Français

  • Graphe d'hoffman-singleton — Schéma du graphe d Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés 7 régulier Diamètre 2 …   Wikipédia en Français

  • Graphe Petersen — Graphe de Petersen Graphe de Petersen Schéma classique du graphe de Petersen, sous la forme d un pentagone et d un pentagramme concentriques, reliés par cinq rayons. Nombre de sommets 10 Nombre d arêtes 15 Distribution des degrés 3 régulier… …   Wikipédia en Français

  • Graphe biparti complet — K3,2 Notation Km,n Nombre de sommets m + n …   Wikipédia en Français

  • Graphe de Tutte–Coxeter — Représentation hamiltonienne du graphe de Tutte–Coxeter. Nombre de sommets 30 Nombre d arêtes 45 Distribution des degrés 3 régulier Rayo …   Wikipédia en Français

  • Graphe distance-régulier — En théorie des graphes, un graphe est distance régulier si pour tous sommets , le nombre de sommets voisins de u à distance i et le nombre de sommets voisins de v à distance j ne dépendent que de i,j et de la distance d(u,v) entre u et v.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”