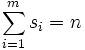- Graphe Partitionable
-
Graphe partitionable
Sommaire
Définitions
Graphe partitionable
Un graphe G est dit partitionable s'il admet une S-partition pour toute partition S de | V | . | V | correspond au cardinal de l'ensemble des sommets de G.
Un graphe G est dit k-partitionable s'il admet une S-partition pour toute k-partition S de | V | .
S-Partition
On note
![[m] = \left \{ 1, ...,m \right \}](/pictures/frwiki/56/8a7d2ca1719bf501188a04854e67b64b.png) .
.Soient G un graphe et
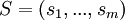 une partition de
une partition de 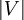 , G est dit admettre une S-partition s'il existe une partition
, G est dit admettre une S-partition s'il existe une partition ![\ P(S)=\left \{V_i : i \in [m]\right \}](/pictures/frwiki/97/ab66b5422dd43b60d2ebd3fe1a6b7135.png) de V telle que :
de V telle que :![\ \forall i \in [m], |V_i| = s_i](/pictures/frwiki/50/25ef80005d7ec7aba967c943dd80c174.png)
![\ \forall i \in [m], G[V_i]](/pictures/frwiki/55/797564fb7763d43a6155b60e64a2e263.png) est un graphe connexe. L'ensemble P(S) est alors dit être une partition de G induite par S.
est un graphe connexe. L'ensemble P(S) est alors dit être une partition de G induite par S.
On considère de plus ici que :
- V est un ensemble non vide
- L'ensemble des arêtes E est un sous-ensemble de l'ensemble des parties à deux éléments de V
Partition d'un entier
Soit n un entier strictement positif, une partition de n est une suite d’entiers
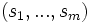 vérifiant
vérifiantUne k-partition de n est une partition de n possédant k éléments.
Exemples
k-partition(n)
- Une 2-partition de 5 est (3,2).
- Une 4-partition de 10 est (1,4,1,4).
- Une 7-partition de 22 est (2,2,3,1,3,8,3).
S-partition de G
- Soit le graphe G tel que V = {a,b,c,d,e,f} et E = { {a,b},{b,c},{c,d},{d,e},{e,f},{f,a},{c,e} } représenté ci-dessous par :
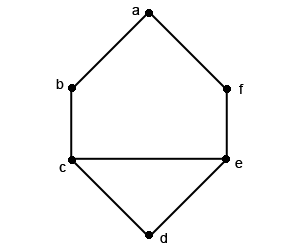
| V | = 6. G admet 3 partitions de 6 possibles : (1,1,4), (1,2,3) et (2,2,2) (en considérant que l'ordre des différentes suites n'a pas d'importance).
Ces trois partitions de l'entier 6 peuvent être appliquées respectivement pour partager le graphe G comme ceci :
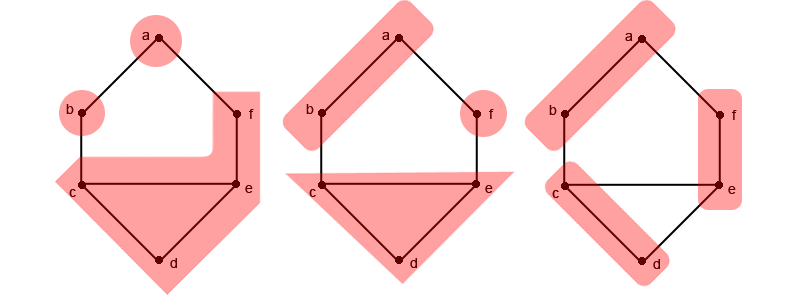
Il existe bien d'autres façon d'appliquer ces 3-partitions sur ce graphe. Le schéma ci-dessus est une des représentations possibles.
- Portail des mathématiques
Catégorie : Concept en théorie des graphes
Wikimedia Foundation. 2010.

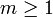
![\ \forall i \in [m] \mbox{ on a } s_i \ne 0](/pictures/frwiki/51/34d2502ba96b639870e1d3acdab8be2d.png)