- Graphe de Kneser
-
Graphe de Kneser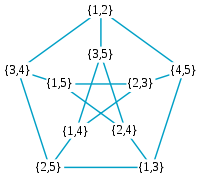 
Le graphe de Kneser KG5,2, isomorphe au graphe de PetersenNotation KGn,k Nombre de sommets 
Distribution des degrés régulier de degré 
Diamètre 
Nombre chromatique n-2k+2 modifier 
En théorie des graphes, les graphes de Kneser forment une famille infinie de graphes. Le graphe de Kneser KGn,k est un graphe simple dont les sommets correspondent aux sous-ensembles à k éléments d'un ensemble à n éléments. Deux sommets sont reliés s'ils correspondent à des sous-ensembles disjoints. Son ordre est donc égal
, le nombre de combinaison de k parmi n, et il est régulier de degré .Sommaire
Histoire
En 1955, le mathématicien Martin Kneser (en) se pose la question suivante : « Si on considère la famille des k-sous-ensembles d'un ensemble de cardinal n, on peut partitionner cette famille en n-2k+2 classes de telle façon qu'aucune paire de k-sous-ensembles dans une classe donnée ne soit disjointe. Est-il possible de partitionner la famille considérée en n-2k+1 classes avec la même propriété ? » Kneser conjecture que ce n'est pas possible et le publie sous forme d'un exercice[1].
En 1978 László Lovász étudie la conjecture de Kneser comme un problème de théorie des graphes[2]. Il introduit les graphes de Kneser puis démontre que le nombre chromatique du graphe KGn,k est égal à n-2k+2, ce qui prouve la conjecture de Kneser. L'approche topologique pour résoudre un problème combinatoire est très novatrice en engendre un nouveau domaine : la combinatoire topologique[3].
Propriétés
Le diamètre d'un graphe de Kneser connexe KGn,k, l'excentricité maximale de ses sommets, est égal à[4] :
Quand
, le graphe de Kneser graph KGn,k est hamiltonien[5]. Il est actuellement conjecturé que tous les graphes de Kneser connexes sont Hamiltoniens sauf KG5,2, le graphe de Petersen. Une recherche exhaustive sur ordinateur a révélé que cette conjecture était vraie pour 
[6],[7].Quand n < 3k, le graphe de Kneser est un graphe sans triangle. Plus généralement, bien que le graphe de Kneser contienne toujours un cycle de longueur 4 quand
, pour des valeurs de n proche de 2k, la longueur du cycle impair le plus court dans le graphe de Kneser est variable[8].Cas particuliers
- Le graphe de Petersen est isomorphe au graphe KG5,2.
- Le graphe complet Kn est isomorphe au graphe KGn,1.
- En 1980, Hall prouve qu'il existe exactement 3 graphes étant localement le graphe de Petersen[9]. Il s'agit du graphe de Conway-Smith, du graphe de Hall et du graphe de Kneser KG7,2.
Voir aussi
Liens internes
Liens externes
- (en) Eric W. Weisstein, Kneser Graph (MathWorld)
- (en) Mitch Keller, Kneser Graphs (PlanetMath)
Références
- Kneser, M. "Aufgabe 300." Jahresber. Deutsch. Math.-Verein 58, 1955.
- Lovász, L. "Kneser's Conjecture, Chromatic Numbers and Homotopy." J. Comb. Th. A 25, 319-324, 1978.
- Mark de Longueville "25 years proof of the Kneser conjecture: The advent of topological combinatorics". EMS Newsletter. Southampton, Hampshire: European Mathematical Society. pp. 16–19. http://emis.kaist.ac.kr/newsletter/current/current9.pdf
- Valencia-Pabon, Mario; Vera, Juan-Carlos, « On the diameter of Kneser graphs », dans Discrete Mathematics, vol. 305, no 1–3, 2005, p. 383–385 [lien DOI]
- Chen, Ya-Chen, « Kneser graphs are Hamiltonian for n ≥ 3k », dans Journal of Combinatorial Theory, Series B, vol. 80, 2000, p. 69–79 [texte intégral, lien DOI]
- (en) Shields, Ian Beaumont, Hamilton Cycle Heuristics in Hard Graphs, Ph.D. thesis, North Carolina State University, 2004 [lire en ligne]
- Shields, I. and Savage, C. D. "A Note on Hamilton Cycles in Kneser Graphs." Bull. Inst. Combin. Appl. 40, 13-22, 2004
- Denley, Tristan, « The odd girth of the generalised Kneser graph », dans European Journal of Combinatorics, vol. 18, no 6, 1997, p. 607–611 [lien DOI]
- Hall, J. I. "Locally Petersen Graphs." J. Graph Th. 4, 173-187, 1980.
Catégorie :- Famille de graphes
Wikimedia Foundation. 2010.
