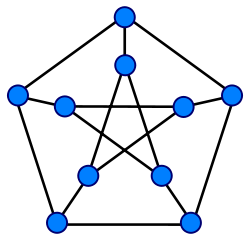
Graphe symétrique

Graphe symétrique
Le Graphe de Petersen est un graphe cubique symétrique.

En théorie des graphes un graphe G est symétrique (ou arc-transitif) si, étant donné deux paires de sommets reliés par une arête u1—v1 et u2—v2 de G, il existe un automorphisme de graphe :

f : V(G) \rightarrow V(G)

tel que

f(u1) = u2 et f(v1) = v2[1].

En d'autres termes, un graphe est symétrique si son groupe d'automorphisme agit transitivement sur ses paires ordonnées de sommets reliés[2]. Un tel graphe est parfois appelé 1-arc-transif[2].

Par définition, un graphe symétrique sans sommet isolé est sommet-transitif [1] et arête-transitif. Le terme symétrique est d'ailleurs parfois employé pour designer un graphe qui soit simplement arête-transitif et sommet-transitif, cette utilisation du terme est ambiguë, car il existe des graphes qui soient arête-transitifs et sommet-transitifs sans êtres arc-transitifs[3]. Dans les cas des graphes d'ordre impair, un graphe arête-transitif et sommet-transitif est cependant nécessairement arc-transitif[4].

Les graphes cubiques symétriques

Un graphe cubique est un graphe régulier dont tous les sommets sont de degré 3. Les graphes cubiques symétriques sont les premiers graphes symétriques intéressants, le cas régulier de degré 2 étant trivial et se résumant aux graphes cycles.

Les graphes cubiques symétriques sont catalogués par Ronald M. Foster à partir de 1934[5]. En 1988 un livre écrit par Ronald M. Foster, I.Z. Bouwer, W.W. Chernoff, B. Monson et Z. Star est publié contenant une liste, alors jugée exhaustive de tous les graphes cubiques symétriques jusqu'à l'ordre 512[6]. Quelques spécimens d'ordre inférieur ou égal à 512 manquent en fait à la liste (les graphes F480B, F432E, F448C, F480C, F480D, F486D, F512D, F512E, F512F, F512G). En 2002, Marston Conder complète la liste et l'étend jusqu'à l'ordre 768[7]. En 2008, une version étendue jusqu'à l'ordre 1320 mais non exhaustive du Foster Census est établie par Alain Bretto et Luc Gillibert[8]

Les premiers graphes cubiques symétriques sont regroupés dans la table suivante :

Ordre Graphe
4 Le graphe tétraédrique (le graphe complet K4)
6 Le graphe biparti complet K3,3
8 Le graphe hexaédrique
10 Le graphe de Petersen
14 Le graphe de Heawood
16 Le graphe de Möbius-Kantor
18 Le graphe de Pappus
20 Le graphe de Desargues
20 Le graphe dodécaédrique

Références

  1. ↑ a et b (en) Biggs, Norman, Algebraic Graph Theory, Cambridge, Cambridge University Press, 1993, 2nd ed.e éd., poche (ISBN 978-0-521-45897-9) (LCCN 94170202), p. 118 
  2. ↑ a et b (en) Godsil, Chris, and Royle, Gordon, Algebraic Graph Theory, New York, Springer, 2001, poche (ISBN 978-0-387-95220-8) (LCCN 00053776), p. 59 
  3. ↑ (en) Bouwer, Z. "Vertex and Edge Transitive, But Not 1-Transitive Graphs." Canad. Math. Bull. 13, 231-237, 1970.
  4. ↑ (en) L Babai, Handbook of Combinatorics, Elsevier, 1996 
  5. ↑ (en) Gordon Royle, Marston Conder , Brendan McKay and Peter Dobscanyi, Cubic symmetric graphs (The Foster Census)
  6. ↑ (en) The Foster Census: R.M. Foster's Census of Connected Symmetric Trivalent Graphs, by Ronald M. Foster, I.Z. Bouwer, W.W. Chernoff, B. Monson and Z. Star (1988) ISBN 0919611192
  7. ↑ (en) Marston Conder, Trivalent symmetric graphs on up to 768 vertices, J. Combin. Math. Combin. Comput, vol. 20, pp. 41-63
  8. ↑ (en) Alain Bretto and Luc Gillibert."G-Graphs: an Efficient Tool for Constructing Symmetric and Semi-Symmetric Graphs". Discrete Applied Mathematics 156 (14) : 2719-2739 (2008).

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Graphe symétrique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Graphe de Nauru — Représentation du graphe de Nauru. Notation F24A Nombre de sommets 24 Nombre d arêtes 36 Distribution des degrés 3 régulier …   Wikipédia en Français

  • Graphe de Hoffman-Singleton — Schéma du graphe de Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés …   Wikipédia en Français

  • Graphe tesseract — Une représentation du graphe tesseract. Nombre de sommets 16 Nombre d arêtes 32 Distribution des degrés 4 régulier Rayon 4 …   Wikipédia en Français

  • Graphe D'Hoffman-Singleton — Schéma du graphe d Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés 7 régulier Diamètre 2 …   Wikipédia en Français

  • Graphe d'Hoffman-Singleton — Schéma du graphe d Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés 7 régulier Diamètre 2 …   Wikipédia en Français

  • Graphe d'hoffman-singleton — Schéma du graphe d Hoffman Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. Nombre de sommets 50 Nombre d arêtes 175 Distribution des degrés 7 régulier Diamètre 2 …   Wikipédia en Français

  • Graphe biparti complet — K3,2 Notation Km,n Nombre de sommets m + n …   Wikipédia en Français

  • Graphe cycle —  Ne doit pas être confondu avec Graphe des cycles ni Cycle (théorie des graphes). Graphe cycle C8 …   Wikipédia en Français

  • Graphe asymétrique — En théorie des graphes, un graphe asymétrique ou graphe identité est un graphe dont le groupe d automorphismes du est d ordre 1. C est donc un graphe n admettant aucun automorphisme autre que l identité. Le plus petit graphe asymétrique est le… …   Wikipédia en Français

  • Graphe de Petersen — Schéma classique du graphe de Petersen, sous la forme d un pentagone et d un pentagramme concentriques, reliés par cinq rayons. Nombre de sommets 10 Nombre d arêtes 15 Distribution des degrés 3 régulier …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”