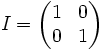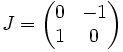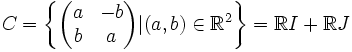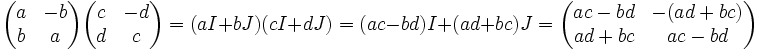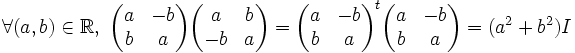- Construction Des Nombres Complexes
-
Construction des nombres complexes
Il existence différentes constructions du corps des nombres complexes, noté en général C ou
. Bien sûr, elles sont toutes équivalentes.Sommaire
Constructions purement algébriques
Définition de Hamilton
Le corps C est défini comme l'ensemble des couples de réels (a,b). Il est muni de deux lois internes, notées + et
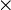(ou l'absence de symbole) définies par:
,
.
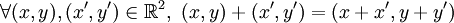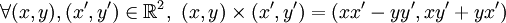Ainsi défini,
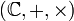est un corps commutatif. L'application de 
dans 
qui a tout réel x associe (x,0) est injective et est un morphisme de corps. Ainsi on identifie x et (x,0) ainsi que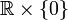 
avec .Dans cettte construction, les racines carrées de -1 sont i = (0,1) et − i = (0, − 1). Par ailleurs,
.
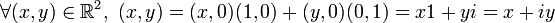C'est l'écriture cartésienne d'un nombre complexe.
Corps de rupture
Article détaillé : corps de rupture.Le polynôme X2+1 ne possède aucune racine réelle (il ne prend que des valeurs supérieures à 1). Le corps C est défini comme le "corps de rupture" du polynôme X2+1, autrement dit comme une extension de R contenant une racine de X2+1. La construction explicite qui suit est un cas particulier d'une construction plus générale donnée dans l'article corps de rupture.
L'ensemble des polynômes à coefficients réels forme une algèbre R[X]. Tout polynôme P(X) s'écrit de manière unique sous la forme
- P(X) = a + bX + (X2 + 1)R(X)
où R est un polynôme. C'est la division euclidienne de P par X2+1. Le reste est aX+b. On note
![\mathbb{C}=\mathbb{R}[X]/(X^2+1)](/pictures/frwiki/97/afe597b4e88f4cc6e31b697729fb3421.png)
l'ensemble des classes de polynômes ayant le même reste dans la division euclidienne par X2+1. La somme et le produit dans R[X] induisent sur C des lois + et :- [a + bX] + [a' + b'X] = [(a + a') + (b + b')X]
![[a+bX]\times [a'+b'X]=[aa'+(ab'+ba')X+bb'X^2]=[(aa'-bb')+(ab'+ba')X^2]](/pictures/frwiki/50/232e5d5dc7751faf210523eb90e82a99.png)
La classe de X est notée i (parfois, par exemple en électricité, les physiciens préfèrent utiliser j, et réservent la lettre i à une intensité). Elle vérifie comme on le souhaitait la relation: i2 = − 1.
Ceci définit une extension des nombres réels, de dimension 2 (on peut donc bien écrire de façon unique tout nombre complexe sous la forme a + bi où a et b sont des réels). On va la munir de la norme euclidienne la plus naturelle dans ce cadre:
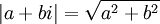. Elle prolonge bien celle des réels, et en tant qu'espace vectoriel de dimension finie sur , on a bien un espace complet.Construction de nature géométrique
Plan d'Argand
Construction matricielle
On note ici
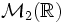l'ensemble des matrices carrées à coefficients réels; on suppose connues les propriétés et la structure de cet ensemble muni des lois d'addition et de multiplication.On s'intéresse aux matrices carrées
et
On considère à présent l'ensemble
L'ensemble C apparait alors comme un sous-espace vectoriel de
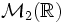de dimension 2 ayant (I,J) pour base.Le calcul habituel sur les matrices donne J2 = − I d'où
On vérifie très simplement que la multiplication laisse stable C et est commutative sur C. Observons de plus que I est l'élément neutre de la multiplication sur les matrices carrées à coefficients réels. L'ensemble C est donc un sous anneau commutatif de
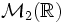.Tout élément non nul de C est inversible; en effet
Le corps
apparait comme isomorphe à un sous corps de C; en identifiant tout réel μ à la matrice scalaire μI, et en posant i = J, on obtient le corps des complexes.Remarques
Pour obtenir le conjugué d'un complexe, il suffit de transposer la matrice qui lui est associée
Le module est obtenu par l'extraction de la racine carrée du déterminant de la matrice qui lui est associée.
Portail des mathématiques
Catégories : Nombre complexe | Théorie des ensembles | Algèbre | Construction classique
Wikimedia Foundation. 2010.
