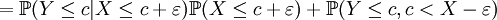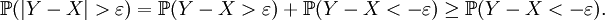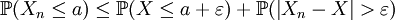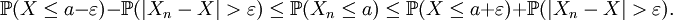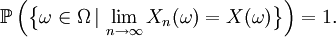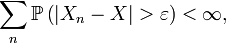- Convergence de variables aleatoires
-
Convergence de variables aléatoires
Dans la théorie des probabilités, il existe différentes notions de convergence de variables aléatoires. La convergence (dans un des sens décrits ci-dessous) de suites de variables aléatoires est un concept important de la théorie des probabilités utilisé notamment en statistique et dans l'étude des processus stochastiques. Par exemple , la moyenne de n variables aléatoires indépendantes et identiquement distribuées converge presque sûrement vers l'espérance commune de ces variables aléatoires. Ce résultat est connu sous le nom de loi forte des grands nombres.
Dans cet article, on suppose que (Xn) est une suite de variables aléatoires réelles, que X est une variable aléatoire réelle, et que toutes ces variables sont définies sur un même espace probabilisé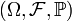 .
.Sommaire
Convergence en loi
Soient F1, F2, ... la suite des fonctions de répartition associées aux variables aléatoires réelles X1, X2, ..., et F la fonction de répartition de la variable aléatoire réelle X.
La suite Xn converge vers X en loi, ou en distribution, si
-
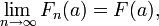 pour tout réel a où F est continue.
pour tout réel a où F est continue.
Puisque F(a) = P(X ≤ a), cela signifie que la probabilité que X appartienne à un certain intervalle est très similaire à la probabilité que Xn soit dans cet intervalle pour n suffisamment grand. La convergence en loi est souvent notée en ajoutant la lettre
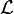 (ou
(ou  pour distribution) au-dessus de la flèche de convergence:
pour distribution) au-dessus de la flèche de convergence:La convergence en loi est la forme la plus faible au sens où, en général, elle n'implique pas les autres formes de convergence définies ci-dessous, alors que ces autres formes de convergence impliquent la convergence en loi. C'est ce type de convergence qui est utilisé dans le théorème de la limite centrale.
Définition équivalente: (Xn) converge en loi vers X ssi pour toute fonction continue bornée
Théorème de continuité de Paul Lévy — Soit
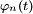 la fonction caractéristique de
la fonction caractéristique de 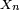 et
et 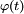 celle de
celle de 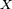 . Alors
. AlorsAutrement dit, (Xn) converge en loi vers X ssi la fonction caractéristique de la variable aléatoire réelle Xn converge simplement vers la fonction caractéristique de la variable aléatoire réelle X.
exemple: Théorème de la limite centrale :La moyenne d'une suite de variables aléatoires centrées, indépendantes et de même loi, une fois renormalisée par
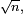 converge en loi vers la loi normaleexemple: convergence de la loi de Student :
converge en loi vers la loi normaleexemple: convergence de la loi de Student :La loi de Student de paramètre
 converge, lorsque
converge, lorsque  tend vers
tend vers  vers la loi de Gauss:
vers la loi de Gauss:Dans ce cas, on peut aussi utiliser le lemme de Scheffé, qui est un critère de convergence d'une suite de variables aléatoires à densité vers une variable aléatoire à densité.
Exemple :La suite[1]
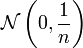 converge en loi vers une variable aléatoire X0 dite dégénérée, qui prend une seule valeur (0) avec probabilité 1 (on parle parfois de masse de Dirac en 0, notée
converge en loi vers une variable aléatoire X0 dite dégénérée, qui prend une seule valeur (0) avec probabilité 1 (on parle parfois de masse de Dirac en 0, notée 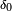 ) :
) :Convergence en probabilité
Définition — On dit que Xn converge vers X en probabilité si,
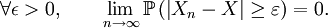
La convergence en probabilité est parfois notée
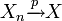 , ou encore
, ou encore 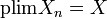
La convergence en probabilité est utilisée dans la loi faible des grands nombres.
La convergence en probabilité implique la convergence en loi. On peut donc énoncer le théorème suivant:
Théorème — Xn converge vers X en probabilité
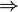 Xn converge vers X en loi.Démonstration
Xn converge vers X en loi.DémonstrationPour effectuer la démonstration, le lemme suivant est utile
Soient X, Y des variables aléatoires réelles, c un réel et ε > 0. Alors
Lemme —
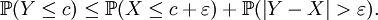 Démonstration du lemme
Démonstration du lemme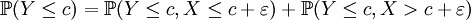
car
Pour tout ε > 0, en raison de ce lemme, on a:
On a donc
Soit a un point de continuité de FX. On fixe un réel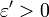 . Par continuité de FX en a, il existe un réel
. Par continuité de FX en a, il existe un réel 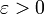 tel que
tel que 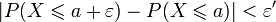 et
et 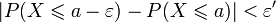 .
.De la convergence de (Xn)n en probabilité vers X, on peut en déduire l'existence d'un entier N tel que :
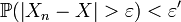 .
.D'où :
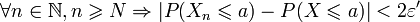 .
.Il existe des conditions suffisantes de convergence en probabilité vers une constante[2], portant sur l'espérance et la variance des termes de la suite :
Théorème —
![\lim_{n \to \infty} \operatorname{E}[X_n]=c\quad \mathbf{ et } \quad \lim_{n \to \infty}\operatorname{Var}[X_n]= 0 \Rightarrow X_n \xrightarrow{p} c](/pictures/frwiki/50/2a6f6e8ad2edf8576f817d4530e0072b.png) .Démonstration
.DémonstrationOn veut montrer que
![\lim_{n \to \infty}\operatorname{E}[X_n]= c\quad \mathbf{ et } \quad \lim_{n \to \infty}\operatorname{Var}[X_n]= 0 \Rightarrow X_n \xrightarrow{p} c](/pictures/frwiki/50/2a6f6e8ad2edf8576f817d4530e0072b.png)
On se sert de l'inégalité de Markov pour les variables aléatoires réelles admettant un moment d'ordre 2 :
Théorème —
![\mathbb{P}\left(\left|U\right| \geq \varepsilon \right) \leq \frac{\operatorname{E}\left[U^2\right]}{\varepsilon^2}\qquad \forall \varepsilon >0.](/pictures/frwiki/50/2b9f00e50d186db7d53e13acbb0b5f3a.png)
D'où :
![\begin{align} \mathbb{P}\left(\left|X_n-c\right| \geq \varepsilon \right)
&\leq \frac{\operatorname{E}\left[(X_n-c)^2\right]}{\varepsilon ^2}\\
&= \frac{\operatorname{Var}(X_n-c)+\left(\operatorname{E}[X_n-c]\right)^2}{\varepsilon ^2}\text{ (formule de Huygens)}\\
&= \frac{\operatorname{Var}(X_n)+\left(\operatorname{E}[X_n]-c\right)^2}{\varepsilon ^2}\\
\end{align}](/pictures/frwiki/50/21eb531a6992254fc1ea61641487bf9f.png)
Il en découle que :
si
![\operatorname{E}[X_n]\to c \quad \mathbf{ et }\quad \operatorname{Var}[X_n]\to 0\text{ alors }\mathbb{P}\left( |X_n -c|\geq\varepsilon\right)\to 0,\text{ donc } X_n \xrightarrow{p} c](/pictures/frwiki/48/020a324e9656aa809e9f5ddc09eb7de4.png) Exemple :
Exemple :Ce théorème est très utile pour démontrer la loi faible des grands nombres de manière simple: il suffit de voir que si
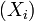 est une suite de variables aléatoires indépendantes et identiquement distribuées d'espérance μ et de variance σ2 et que
est une suite de variables aléatoires indépendantes et identiquement distribuées d'espérance μ et de variance σ2 et que  , alors:
, alors:![\operatorname{E}[\bar{X}_n]=\mu](/pictures/frwiki/50/22bcfe41117d0857580c71852d74eb12.png)
![\lim_{n\to\infty}\operatorname{Var}[\bar{X}_n]=\lim_{n\to\infty}\frac{\sigma^2}{n}=0\qquad](/pictures/frwiki/56/873308dd3c766f52264fc3242c3d6203.png) (voir preuve sur la page variance)
(voir preuve sur la page variance)
Donc
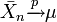
La réciproque n'est pas vraie :
- En statistiques, un estimateur peut être biaisé mais cependant convergent !
- Dans l'exemple suivant, la suite, d'espérance constante, converge vers une constante différente de cette espérance ; la suite des variances tend vers l'infini.
Exemple :Soit une suite
 de variables aléatoires telle que chaque Xn prenne pour valeurs 0 et n et que :
de variables aléatoires telle que chaque Xn prenne pour valeurs 0 et n et que :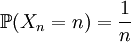 , donc
, donc 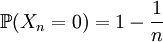 .
.
On voit qu'elle converge en probabilité :
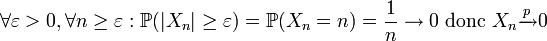 .
.Cependant,
![\operatorname{E}[X_n]=1](/pictures/frwiki/101/e97947bace53c8f30865c87398f213e9.png) et
et ![\operatorname{Var}[X_n]=n-1\to +\infty](/pictures/frwiki/97/a58df8265cbaa761b1c87a120f28d62e.png) .
.Ainsi les conditions énoncées plus haut de convergence en probabilité vers une constante ne sont pas nécessaires[3].
Convergence presque sûre
On dit que Xn converge presque sûrement ou presque partout ou avec probabilité 1 ou fortement vers X si
Définition —
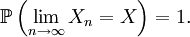
Cela signifie que les valeurs de Xn approchent la valeur de X, au sens où (cf. presque partout) l'événement sur lequel Xn ne converge pas vers X a une probabilité nulle.
On note souvent cela
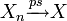 ou
ou  (almost surely en anglais).
(almost surely en anglais).On peut expliciter la définition de la convergence presque sûre en utilisant l'espace probabilisé
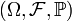 et le concept de variable aléatoire comme fonction de Ω dans
et le concept de variable aléatoire comme fonction de Ω dans  :
:Théorème — Xn converge vers X presque sûrement
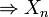 converge vers X en probabilité
converge vers X en probabilitéLa convergence presque sûre est utilisée dans la loi forte des grands nombres.
Convergence en moyenne d'ordre r
Soit r > 0. On dit que Xn converge vers X en moyenne d'ordre r ou en norme Lr si E|Xn|r < ∞ pour tout n et
-
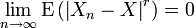 .
.
La convergence en moyenne d'ordre r nous dit que l'espérance de la puissance r-ième de la différence entre Xn et X converge vers zéro.
Pour r =2, on parle de convergence en moyenne quadratique
Théorème — Xn converge vers X en norme Lr
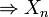 converge vers X en probabilité.Démonstration
converge vers X en probabilité.DémonstrationOn se sert de l'inégalité de Markov pour les variables aléatoires réelles admettant un moment d'ordre r :
Théorème —
![\mathbb{P}\left(\left|U\right| \geq \varepsilon \right) \leq \frac{\operatorname{E}\left[|U|^r\right]}{\varepsilon^r}\qquad \forall \varepsilon >0.](/pictures/frwiki/57/96f43047765d306e6f6e67c5723839d3.png)
On a donc :
![\mathbb{P}\left(\left|X_n-X\right| \geq \varepsilon \right) \leq \frac{\operatorname{E}[\left|X_n-X\right|^r]}{\varepsilon^r}](/pictures/frwiki/49/16cb3f9613ce960a660ad0d0f197c72e.png) , d'où découle le résultat annoncé.
, d'où découle le résultat annoncé.Théorème — Pour r > s ≥ 1, la convergence en norme Lr implique la convergence en norme Ls.
On a également le résultat suivant:
Théorème — Xn converge vers une constante c en moyenne quadratique
![\Leftrightarrow \left\{\lim_{n \to \infty}\operatorname{E}[X_n]=c\quad\mathbf{et}\quad \lim_{n \to \infty}\operatorname{Var}[X_n]=0\right\}](/pictures/frwiki/102/f232b573c7bdc039f724c9db7836f2bd.png) .Démonstration
.DémonstrationOn a vu plus haut que :
![\operatorname{E}\left[(X_n-c)^2\right] = \operatorname{Var}(X_n)+\left(\operatorname{E}[X_n]-c\right)^2](/pictures/frwiki/51/35ddd76e71c05d3143965ea777a403bd.png)
Convergence d'une fonction d'une variable aléatoire
Un théorème très pratique, désigné en anglais généralement sous le nom de Mapping theorem (en), établit qu'une fonction g continue appliquée à une variable qui converge vers X convergera vers g(X) pour tous les modes de convergence:
Théorème — Mapping theorem[4] Soit
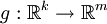 une fonction continue en tout point d'un ensemble C tel que
une fonction continue en tout point d'un ensemble C tel que 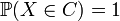 :
:- Si

- Si
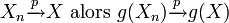
- Si
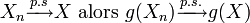
Exemple :En statistiques, un estimateur convergent de la variance σ2 est donné par:
On sait alors par le continuous mapping theorem que l'estimateur
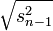 de l'écart type
de l'écart type  est convergent, car la fonction racine est une fonction continue.
est convergent, car la fonction racine est une fonction continue.Implications réciproques
À quelques exceptions près, les implications mentionnées dans les sections précédentes n'ont pas de réciproque, à proprement parler. Voici toutefois quelques propriétés utiles qu'on pourrait qualifier de "semblants de réciproques":
- Si Xn converge en loi vers une constante réelle c, alors Xn converge en probabilité vers c.
- Si Xn converge presque sûrement vers X, alors Xn converge en loi vers X, et la réciproque est fausse, mais il existe un théorème (appelé "théorème de représentation de Skorohod") qui est une forme de réciproque, voir, dans Fonction de répartition, la section Convergence en loi et fonction de répartition, et particulièrement (1. implique 3.).
- Si Xn converge en probabilité vers X, et si P(|Xn| ≤ b) = 1 pour tout n et un certain b, alors Xn converge en moyenne d'ordre r vers X pour tout r ≥ 1. Autrement dit,
- Si Xn converge en probabilité vers X et si toutes les variables aléatoires Xn sont uniformément presque sûrement bornées, alors Xn converge vers X en moyenne d'ordre r.
- Si pour tout ε > 0,
alors Xn converge presque sûrement vers X. En d'autres termes, si Xn converge en probabilité vers X suffisamment rapidement (i.e. la série ci-dessus converge pour tout ε > 0), alors Xn converge aussi presque sûrement vers X. Cela résulte d'une application directe du théorème de Borel-Cantelli.
- Soit
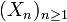 une suite de variables aléatoires réelles indépendantes. Pour tout n, on pose :
une suite de variables aléatoires réelles indépendantes. Pour tout n, on pose :
-
 .
.
Alors la convergence presque sûre de la suite
 équivaut à sa convergence en probabilité ; autrement dit, la convergence presque sûre de la série de terme général Xn équivaut à sa convergence en probabilité.
équivaut à sa convergence en probabilité ; autrement dit, la convergence presque sûre de la série de terme général Xn équivaut à sa convergence en probabilité.Notes
- ↑ Pour plus de détail sur cet exemple: voir Davidson et McKinnon (1993, chap. 4)
- ↑ Ce sont en fait des conditions nécessaires et suffisantes de convergence en moyenne quadratique vers cette même constante, cf. infra.
- ↑ En fait, cet exemple montre qu'une suite de variables aléatoires réelles peut converger en probabilité vers une constante sans converger en moyenne quadratique.
- ↑ Tiré de Vaart (1998, p.7)
Références
- (en) Russell Davidson, Estimation and Inference in Econometrics, Oxford University Press, New York (ISBN 0195060113), p. 874
- G.R. Grimmett and D.R. Stirzaker (1992). Probability and Random Processes, 2nd Edition. Clarendon Press, Oxford, p. 271-285 (ISBN 0-19-853665-8)
- (en) Adrianus Willem van der Vaart, Asymptotic Statistics, Cambridge University Press, Cambridge (ISBN 0521496039), p. 443
- Portail des probabilités et des statistiques
Catégorie : Probabilités -
Wikimedia Foundation. 2010.

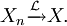
![\lim_{n\rightarrow\infty} E[f(X_n)]=E [f(X)].](/pictures/frwiki/52/4df277188d111e3ffb3a55fbcc53e237.png)
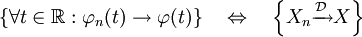
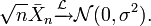
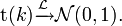
![\mathbb{P}(X_0\le x)=\delta_0\left(]-\infty,x]\right)=\begin{cases}0 & \text{ si } x< 0,\\1 &\text{ si } x \geq 0.\end{cases}](/pictures/frwiki/53/558cc28ff14794779ac82a1bf2e028e1.png)