Inegalite de Markov
- Inegalite de Markov
-
Inégalité de Markov
En théorie des probabilités, l'inégalité de Markov donne une borne supérieure de la probabilité qu'une variable aléatoire à valeurs positives soit supérieure ou égale à une constante positive. Cette inégalité a été nommée ainsi en l'honneur d'Andrei Markov.
Énoncé
Démonstration
On a l'inégalité
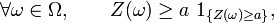
dès que 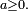 On en déduit que
On en déduit que
![\mathbb{E}[Z]\ \ge\ \mathbb{E}[a\ 1_{\{Z\ge a\}}]\ \left({\scriptstyle\ =\ a\ \mathbb{P}(Z\ge a)}\ \right).](/pictures/frwiki/57/9818c4f0b1093ceca67216b86c189191.png)
Corollaire
Elle possède un corollaire fréquemment utilisé:
Applications
Voir aussi
 Portail des probabilités et des statistiques
Portail des probabilités et des statistiques
Catégories : Probabilités | Inégalité
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Inegalite de Markov de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Inégalité De Markov — En théorie des probabilités, l inégalité de Markov donne une borne supérieure de la probabilité qu une variable aléatoire à valeurs positives soit supérieure ou égale à une constante positive. Cette inégalité a été nommée ainsi en l honneur d… … Wikipédia en Français
Inégalité de markov — En théorie des probabilités, l inégalité de Markov donne une borne supérieure de la probabilité qu une variable aléatoire à valeurs positives soit supérieure ou égale à une constante positive. Cette inégalité a été nommée ainsi en l honneur d… … Wikipédia en Français
Inégalité de Markov — En théorie des probabilités, l inégalité de Markov donne une borne supérieure de la probabilité qu une variable aléatoire à valeurs positives soit supérieure ou égale à une constante positive. Cette inégalité a été nommée ainsi en l honneur d… … Wikipédia en Français
Inegalite de Bienayme-Tchebychev — Inégalité de Bienaymé Tchebychev Soit X une variable aléatoire d espérance μ et de variance finie σ2 (l hypothèse de variance finie garantit l existence de l espérance). L inégalité de Bienaymé Tchebychev s énonce de la façon suivante :… … Wikipédia en Français
Inégalité De Bienaymé-Tchebychev — Soit X une variable aléatoire d espérance μ et de variance finie σ2 (l hypothèse de variance finie garantit l existence de l espérance). L inégalité de Bienaymé Tchebychev s énonce de la façon suivante : Théorème pour tout réel… … Wikipédia en Français
Inégalité de bienaymé-tchebychev — Soit X une variable aléatoire d espérance μ et de variance finie σ2 (l hypothèse de variance finie garantit l existence de l espérance). L inégalité de Bienaymé Tchebychev s énonce de la façon suivante : Théorème pour tout réel… … Wikipédia en Français
MARKOV (A. A.) — MARKOV ANDREÏ ANDREÏEVITCH (1856 1922) Mathématicien russe né à Riazan et mort à Petrograd. Andreï Andreïevitch Markov est connu comme un spécialiste de la théorie des nombres, de la théorie des probabilités et de l’analyse mathématique. Issu… … Encyclopédie Universelle
Inégalité d'Azuma — L’inégalité d Azuma, parfois appelée inégalité d Azuma Hoeffding, est une inégalité de concentration concernant les martingales dont les accroissements sont bornés. C est une généralisation de l inégalité de Hoeffding, une inégalité de… … Wikipédia en Français
Inégalité de Hoeffding — L’inégalité de Hoeffding est une inégalité de concentration concernant les sommes de variables aléatoires indépendantes et bornées. Il existe une version plus générale de cette inégalité, concernant une somme d accroissements de martingales,… … Wikipédia en Français
Inégalité de Bienaymé-Tchebychev — Soit X une variable aléatoire d espérance μ et de variance finie σ2 (l hypothèse de variance finie garantit l existence de l espérance). L inégalité de Bienaymé Tchebychev s énonce de la façon suivante : Théorème Pour tout réel… … Wikipédia en Français
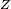 une variable aléatoire réelle définie sur un espace probabilisé
une variable aléatoire réelle définie sur un espace probabilisé 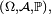 et supposée presque sûrement positive ou nulle. Alors
et supposée presque sûrement positive ou nulle. Alors![\forall a >0,\qquad \mathbb P(Z\geq a)\leq\frac{\mathbb{E}[Z]}{a}.](/pictures/frwiki/55/7c047168b606d56dccbe54e1fb5c2c20.png) Démonstration
Démonstration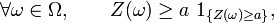
 On en déduit que
On en déduit que![\mathbb{E}[Z]\ \ge\ \mathbb{E}[a\ 1_{\{Z\ge a\}}]\ \left({\scriptstyle\ =\ a\ \mathbb{P}(Z\ge a)}\ \right).](/pictures/frwiki/57/9818c4f0b1093ceca67216b86c189191.png)
 une fonction croissante et positive ou nulle sur l'intervalle
une fonction croissante et positive ou nulle sur l'intervalle  Soit
Soit 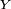 une variable aléatoire réelle définie sur un espace probabilisé
une variable aléatoire réelle définie sur un espace probabilisé 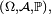 et telle que
et telle que 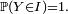 Alors
Alors![\forall b \in I,\text{ tel que }\phi(b)>0,\qquad \mathbb P(Y\geq b)\leq\frac{\mathbb{E}[\phi(Y)]}{\phi(b)}.](/pictures/frwiki/102/f34e85d3c6dbb0093f87dd42ab3c531c.png) Démonstration
Démonstration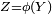 et à
et à 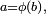 pour obtenir que
pour obtenir que![\forall b >0,\qquad \mathbb P(\phi(Y)\geq \phi(b))\leq\frac{\mathbb{E}[\phi(Y)]}{\phi(b)}.](/pictures/frwiki/98/b5972aba772cbc00c95abfda32121437.png)
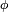 entraine que
entraine que 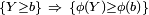 et donc que
et donc que 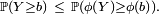
![\scriptstyle\ Y=|X-\mathbb{E}[X]|,\](/pictures/frwiki/98/b8fbde8e90bac6199a3ad942ff10fbfa.png)
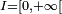 et
et 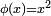 donne l'inégalité de Bienaymé-Tchebychev.
donne l'inégalité de Bienaymé-Tchebychev.![\scriptstyle\ Y=X-\mathbb{E}[X],\](/pictures/frwiki/53/57400e7b2a7af49cf6646ccbaa4ad5af.png) ou bien
ou bien ![\scriptstyle\ Y=\mathbb{E}[X]-X,\](/pictures/frwiki/100/d12bc4f04b5f9116224950c9f52d7468.png)
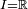 et
et 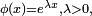 donne l'inégalité de Chernoff ou l'inégalité de Hoeffding.
donne l'inégalité de Chernoff ou l'inégalité de Hoeffding.