Facteur premier

En mathématiques et plus précisément en arithmétique modulaire, la décomposition en produit de facteurs premiers (aussi connue comme la factorisation entière en nombres premiers) est le problème suivant : soit un entier strictement positif, comment l'écrire sous forme d'un produit de nombres premiers. Par exemple, si le nombre donné est 45, la factorisation en nombres premiers est 3²·5.

Par définition, un nombre premier ne peut pas être décomposé. On peut aussi dire qu'il est sa propre décomposition.

11 = 11

25 = 5 × 5 = 5²

125 = 5 × 5 × 5 = 5³

360 = 2 × 2 × 2 × 3 × 3 × 5 = 2³ × 3² × 5

1 001 = 7 × 11 × 13

1 010 021 = 17 × 19 × 53 × 59

La factorisation est toujours unique, en accord avec le théorème fondamental de l'arithmétique. Ce problème est d'une importance considérable en mathématiques, en cryptologie, en théorie de la complexité, et pour les calculateurs quantiques.

Décomposition en nombres premiers

Tout nombre naturel n non nul peut s'écrire de manière unique comme le produit fini de nombres premiers à une puissance adéquate.

.

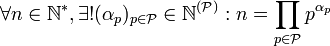La liste complète des facteurs peut être déduite de la factorisation en nombres premiers en incrémentant les exposants de zéro jusqu'au nombre cherché. Par exemple, comme 45 = 3²·5, 45 est divisible par 3⁰·5⁰, 3⁰·5¹, 3¹·5⁰, 3¹·5¹, 3²·5⁰, et 3²·5¹, ou 1, 5, 3, 15, 9, et 45. Par contraste, la factorisation en nombres premiers inclut seulement les facteurs premiers. Voir l'algorithme de décomposition en produit de facteurs premiers.

Applications pratiques

Soient deux grands nombres premiers donnés, il est facile d'en obtenir le produit. Par contre, il est beaucoup plus difficile de trouver les facteurs premiers de celui-ci. C'est ce que l'on appelle une fonction trappe. Ceci s'applique pour les systèmes modernes en cryptologie. Si une méthode rapide était trouvée pour résoudre le problème de la factorisation des nombres entiers, alors plusieurs systèmes cryptologiques importants seraient cassés, incluant l'algorithme à clé publique RSA et le générateur de nombres pseudo-aléatoires Blum Blum Shub. La mise au point d'un ordinateur quantique est une de ces méthodes.

Bien que la factorisation soit une manière de casser ces systèmes, il peut exister d'autres manières de les casser qui n'impliquent pas la factorisation. Ainsi, il est possible que le problème de la factorisation entière soit vraiment difficile, ces systèmes peuvent quand même être cassés rapidement. Une exception rare est le générateur Blum Blum Shub. Il a été prouvé qu'il est exactement aussi difficile que la décomposition en produit de facteurs premiers : si vous pouvez casser le générateur en temps polynomial alors, vous pouvez factoriser les entiers en temps polynomial, et vice versa.

État actuel de l'art

Si un grand nombre à n-bit est le produit de deux nombres premiers qui sont probablement de la même taille, alors aucun algorithme n'est actuellement connu pour pouvoir le factoriser en temps polynomial. Ce qui veut dire qu'il n'existe pas d'algorithme connu pouvant le factoriser en temps O(n^k) quelle que soit la constante k. Il existe des algorithmes, néanmoins, qui sont aussi rapides que Θ(eⁿ). En d'autres termes, les meilleurs algorithmes connus sont sous-exponentiels, mais super-polynômiaux. En particulier, le meilleur algorithme connu s'exécutant en temps asymptotique est le crible général de corps de nombres (GNFS).

Pour un ordinateur ordinaire, GNFS est le meilleur algorithme connu pour les grands n. Pour un calculateur quantique, par contre, Peter Shor a découvert un algorithme en 1994 qui le résout en temps polynomial ! Ceci aura des implications significatives pour la cryptologie si un grand calculateur quantique est construit un jour. L'algorithme de Shor prend seulement O(n³) de temps et O(n) d'espace. Les formes de l'algorithme sont connues pour utiliser seulement 2n qubits. En 2001, le premier calculateur quantique 7-qubit devint le premier à exécuter l'algorithme de Shor. Il factorisa le nombre 15 (!).

Difficulté et complexité

On ne connaît pas exactement quelles classes de complexité contiennent le problème de la décomposition en produit de facteurs premiers. Le problème de décision de forme ("N a-t-il moins de facteurs que M ?") est connu pour être à la fois NP et co-NP. Ceci parce que les réponses OUI et NON peuvent être cochées si les facteurs premiers sont donnés avec leurs preuves de primalité. Il est connu comme étant dans BQP à cause de l'algorithme de Shor. Il est suspecté d'être en dehors des trois classes de complexité P, NP-complet, et co-NP-complet. S’il peut être démontré qu'il est soit NP-Complet ou co-NP-Complet, cela impliquerait NP = co-NP. Ce serait un résultat très surprenant, par conséquent la factorisation entière est largement suspectée d'être en dehors de ces classes. Beaucoup de monde ont essayé de trouver des algorithmes en temps polynomial pour cela et ont échoué, par conséquent, elle est largement suspectée d'être en dehors de P.

De manière intéressante, le problème de décision « N est-il un nombre composé ? » (ou de façon équivalente : « N est-il un nombre premier ? ») apparaît comme étant plus facile que le problème consistant à trouver les facteurs de N. Plus précisément, la question ci-dessus peut être résolue en temps polynomial (en nombre n des chiffres de N), en accord avec l'article récent donné dans les références ci-dessous. De plus, il existe un nombre d'algorithmes probabilistes qui peuvent tester la primalité d'un nombre très rapidement si l'un d'eux est susceptible d'accepter une petite possibilité d'erreur. La facilité de test d'un nombre premier est une partie cruciale de l'algorithme RSA, comme il est nécessaire de trouver de grands nombres premiers pour démarrer avec lui.

Algorithmes de factorisation

But spécial

Les temps d'exécution des algorithmes de factorisation à but spécial dépend des propriétés de ses facteurs inconnus : taille, forme spéciale, etc. De manière exacte, le temps d'exécution dépend de ce qui varie entre les algorithmes.

• Essais de divisions
• Algorithme rho de Pollard
• Algorithme p-1 de Pollard
• Factorisation en courbe elliptique de Lenstra
• Congruence de carrés (Méthode de factorisation de Fermat)
• Crible spécial de corps de nombres (SNFS)

But général

Le temps d'exécution des algorithmes de factorisation à but général dépend seulement de la taille de l'entier à factoriser. Ceci est le type d'algorithme utilisé pour factoriser les nombres RSA. La plupart des algorithmes de factorisation à but général sont basés sur la méthode des congruence de carrés.

• Crible quadratique
• Crible général de corps de nombres (GNFS)

Liens externes

• (en) Article « PRIMES is in P »L'article de Manindra Agrawal, Nitin Saxena, Neeraj Kayal qui montre que déterminer si un nombre est premier est un problème de complexité polynomial (PDF)
• (fr) Applet Java basé sur le travail de Alejandro Alpern
• (en) http://www.alpertron.com.ar/ECM.HTM est une applet Java de factorisation entière qui utilise la méthode des courbes elliptiques et le crible quadratique d'auto-initialisation (Self Initializing Quadratic Sieve) (en anglais).
• programme de factorisation entière du domaine public pour Windows Il peut prendre en charge des nombres de 80 chiffres. Voir aussi le site web pour MIRACL

• Portail des mathématiques