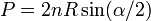- Calcul de l'aire d'un polygone
-
Polygone
Pour les articles homonymes, voir Polygone (homonymie).En géométrie euclidienne, un polygone (du grec polus, nombreux, et gônia, angle) est une figure géométrique plane, formée d'une suite de segments, chacun d'entre eux partageant une extrémité avec le précédent et le suivant, délimitant ainsi un contour fermé. Le terme polygone recouvre en particulier les figures fermées délimitées par une ligne brisée (une figure en forme d'étoile par exemple).
La notion de polygone est généralisée par celles de polyèdre, de polytope et de ligne brisée.
Des polygones
Vocabulaire de base
Soient A1, A2, A3, ... An, n points d'un plan. On dénomme alors polygone la figure notée « A1A2A3...An », et constituée par la suite des n segments : [A1A2], [A2A3], ... [An-1An] et [AnA1].
Les n points précédents sont les sommets du polygone, et les n segments ses côtés. À chaque sommet est associé un angle, c'est l'angle entre les deux côtés qui aboutissent au sommet.
Ordre d'un polygone
Le nombre n des côtés d'un polygone est communément appelé ordre de ce polygone. C'est évidemment aussi le nombre de ses sommets ou celui de ses angles. Par exemple, un polygone d'ordre cinq détient cinq sommets, cinq angles et cinq côtés.
Eléments opposés
- Si l'ordre d'un polygone est pair :
-
-
- les sommets séparés par n/2 côtés sont dits « opposés » entre eux ;
- même chose pour les angles correspondants ;
- les côtés séparés par n/2 sommets sont dits eux aussi « opposés » entre eux.
-
- Si l'ordre du polygone est impair, les côtés sont « opposés » aux sommets et aux angles ( et vice versa ) ; plus précisément, chaque sommet ( ou chaque angle ) est « opposé » au côté situé (n - 1)/2 sommets plus loin.
Côtés prolongés et diagonales
Les droites qui portent les côtés d'un polygone sont appelées les côtés prolongés de ce polygone.
Les côtés d'un polygone ne sont pas les seuls segments qui peuvent relier les sommets entre eux. Tout segment reliant deux sommets d'un polygone et autre qu'un côté est appelé diagonale de ce polygone.
Un polygone à n côtés possède ainsi
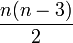diagonales.Typologie des polygones
Il existe de nombreuses manières de classer les polygones : en fonction de leur convexité, de leurs symétries, de leurs angles... Mais on les classe d'abord suivant leur nombre de côtés.
Classement suivant le nombre de côtés
Les polygones peuvent être classés entre eux suivant leur nombre de côtés, c'est-à-dire leur ordre.
Le polygone le plus élémentaire est le triangle : un polygone possède au moins trois sommets et trois côtés.
Vient ensuite le quadrilatère, à quatre côtés et quatre sommets.
À partir de l'ordre cinq, chaque nom de polygone est formé d'une racine grecque correspondant à l'ordre du polygone suivie du suffixe -gone.
Pour s'y retrouver dans la dénomination des polygones, il faut retenir que -kai- signifie « plus » en grec, et que -conta- signifie « dizaine ». Par exemple, le mot triacontakaiheptagone signifie trois (tria-) dizaines (-conta-) plus (-kai-) sept (-hepta-) unités, et correspond donc à un polygone de trente-sept côtés.
Au-delà de douze côtés, la coutume incite à parler de polygone à n côtés où n est remplacé par le nombre souhaité, ceci afin de simplifier les choses.
Il existe cependant plusieurs dénominations anciennes pour des nombres « ronds » comme pour un polygone à vingt côtés (icosa-), à cent côtés (hecto-) et à dix mille côtés (myria-).
Dénominations des polygones Nombre de côtés Nom hénagone ou monogone polygone à 1 côté, objet impossible en géométrie euclidienne [1] digone ou angle un polygone dégénéré à 2 côtés 3 côtés triangle ou trigone 4 côtés quadrilatère ou tétragone 5 côtés pentagone 6 côtés hexagone 7 côtés heptagone 8 côtés octogone 9 côtés ennéagone ou nonagone 10 côtés décagone 11 côtés hendécagone 12 côtés dodécagone 13 côtés triskaidécagone ou tridécagone 14 côtés tétrakaidécagone ou tétradécagone, quadridécagone 15 côtés pentakaidécagone ou pentadécagone, quidécagone 16 côtés hexakaidécagone ou hexadécagone 17 côtés heptakaidécagone ou heptadécagone 18 côtés octakaidécagone ou octadécagone 19 côtés ennéakaidécagone ou ennéadécagone 20 côtés icosagone 21 côtés icosikaihenagone ou henicosagone 22 côtés icosikaidigone ou doicosagone 23 côtés icosikaitrigone ou triaicosagone 24 côtés icosikaitétragone ou tétraicosagone 25 côtés icosikaipentagone ou pentaicosagone 26 côtés icosikaihexagone ou hexaicosagone 27 côtés icosikaiheptagone ou heptaicosagone 28 côtés icosikaioctagone ou octaicosagone 29 côtés icosikaiennéagone ou ennéaicosagone 30 côtés triacontagone 31 côtés triacontakaihenagone ou hentriacontagone 32 côtés triacontakaidigone ou dotriacontagone 33 côtés triacontakaitrigone ou tritriacontagone 34 côtés triacontakaitétragone ou tétratriacontagone 35 côtés triacontakaipentagone ou pentatriacontagone 36 côtés triacontakaihexagone ou hexatriacontagone 37 côtés triacontakaiheptagone ou heptatriacontagone 38 côtés triacontakaioctogone ou octatriacontagone 39 côtés triacontakaiennégone ou ennéatriacontagone 40 côtés tétracontagone 50 côtés pentacontagone 60 côtés hexacontagone 70 côtés heptacontagone 80 côtés octacontagone 90 côtés ennéacontagone 100 côtés hectogone ou hécatontagone 200 côtés dihectogone 300 côtés trihectogone 400 côtés tétrahectogone 500 côtés pentahectogone 600 côtés hexahectogone 700 côtés heptahectogone 800 côtés octahectogone 900 côtés ennéahectogone 1 000 côtés chiliogone ou chiliagone ou chiligone[2] 10 000 côtés myriagone ou myriogone[2] Les mêmes principes s'appliquent aux polyèdres, où il suffit de remplacer le suffixe -gone par le suffixe -èdre.
Classement par convexité
On rappelle qu'une diagonale d'un polygone est un segment qui joint deux sommets non consécutifs, c'est-à-dire un segment qui joint deux sommets et qui n'est pas un côté du polygone.
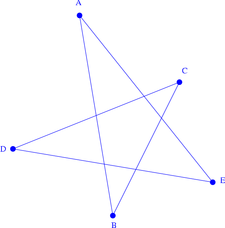
Pentagone croisé.Exemple : les segments [AC], [AD], [BD], [BE], [CE] sont les 5 diagonales du pentagone ABCDE ci-contre.
Polygone croisé
Un polygone est dit croisé si au moins deux de ses côtés sont sécants, c'est-à-dire si au moins deux de ses côtés se coupent. C'est le cas du pentagone ABCDE ci-contre (à droite).
L' enveloppe d'un polygone est le polygone obtenu en suivant le contour extérieur de celui-ci. Par exemple, l'enveloppe du pentagone précédent est un décagone dont les sommets sont les cinq sommets du pentagone et les cinq intersections de ses côtés.
Polygone concave
Polygone concave.Un polygone est dit concave s'il n'est pas croisé et si l'une de ses diagonales n'est pas entièrement à l'interieur de la surface délimitée par le polygone.
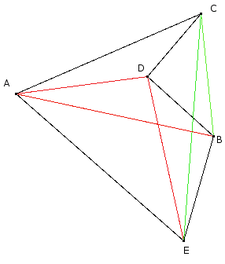
Par exemple, le pentagone ACDBE ci-contre ( à droite ) est dit concave car les diagonales [BC] et [CE] sont à l'extérieur de la surface délimitée par le polygone.
Polygone convexe
Polygone convexe.Un polygone est dit convexe s'il n'est pas croisé et si toutes ses diagonales sont entièrement à l'intérieur de la surface délimitée par le polygone. Ainsi, l'hexagone MNOPQR ci-contre (à droite) est dit convexe.
Polygone étoilé
L' enveloppe convexe d'un polygone est le plus petit polygone convexe le contenant. Attention : l'enveloppe et l'enveloppe convexe d'un polygone ne se confondent que si celui-ci est convexe !
Un polygone est alors dit étoilé si (et seulement si) aucun de ses côtés n'appartient à son enveloppe convexe.
Par exemple, le pentagone croisé précédent et son enveloppe sont étoilés tous les deux.
Classement par symétrie
Notion d'élément de symétrie
Un polygone peut présenter des régularités (appelées symétries) qui le rendent globalement invariant par certaines transformations telles que des rotations ou des réflexions. L'élément de symétrie d'une transformation est l'ensemble des points invariants par cette transformation :
- pour une symétrie centrale, l'élément de symétrie est le centre de symétrie ;
- pour une symétrie axiale, l'élément de symétrie est justement cet axe, dit axe-miroir car il coupe toute figure globalement invariante par cette transformation en deux parties images en miroir l'une de l'autre ;
- pour une rotation, l'élément de symétrie est le centre de rotation. Pour définir précisément une rotation, il faut préciser, outre son centre de rotation, son angle. On peut aussi définir une rotation en donnant son centre et son ordre, qui indique combien de fois il faut appliquer la rotation pour revenir au point de départ. Il existe des rotations d'ordre infini, mais lorsqu'il est fini, son produit avec l'angle de la rotation est toujours égal à un multiple de 2 π radians (ou 1 tour ou 360°...).
On peut remarquer que, dans le plan, la symétrie centrale se confond avec la rotation d'ordre deux.
On dit qu'un polygone (ou plus généralement toute figure de géométrie) présente un élément de symétrie quand il est globalement invariant par la transformation correspondante.
Dans le cas d'un polygone, tous les éléments de symétrie passent par un même point. Lorsqu'il est unique, ce point est appelé centre du polygone.
Lien avec la théorie des groupes
L'ensemble des symétries d'un polygone (ou en fait de tout autre objet géométrique) est un exemple typique de groupe. En effet, lorsqu'on compose deux symétries d'un polygone (c'est-à-dire qu'on effectue l'une puis l'autre) le résultat est encore une symétrie de ce polygone, la composition forme donc une loi de groupe sur l'ensemble des symétries d'un polygone. Ainsi la théorie des groupes permet-elle une étude simple et générale des symétries d'un polygone.
Notion de polygone régulier
Un polygone est dit régulier s'il est convexe et présente un axe de rotation d'ordre égal à son nombre de côtés.
Ennéagone régulier.Cela signifie qu'il se superpose à lui-même quand on le tourne d'un angle de
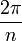, où n est l'ordre du polygone.Le polygone présente ainsi la même configuration en chacun de ses sommets qui sont donc disposés régulièrement sur un cercle centré sur l'axe de rotation.
Un polygone régulier est donc un polygone convexe inscrit dans un cercle et dont tous les côtés ont la même longueur (et les angles la même mesure).
Inversement, si un polygone convexe est inscriptible dans un cercle et si ses côtés sont égaux (ou ses angles égaux ), alors il est régulier.
L'ensemble des symétries d'un polygone régulier est appelé un groupe dihédral.
Quelques exemples et contre-exemples :
- le triangle équilatéral est un polygone régulier ;
- le carré est un polygone régulier ;
- le losange (non carré) n'est pas régulier (il n'est pas inscriptible dans un cercle).
Polygone isocèle
Polygone isocèle d'ordre impair (triangle isocèle).Un polygone est dit isocèle quand il présente au moins un axe-miroir.
Les axes-miroirs passent nécessairement par des sommets ou des milieux des côtés du polygone.
Plus précisément :
- si l'ordre du polygone est impair, tout axe-miroir passe par un sommet et le milieu du côté opposé ( médiane, voir plus bas );
- si l'ordre du polygone est pair, tout axe-miroir passe soit par deux sommets opposés ( diagonale principale, voir plus bas ), soit par les milieux de deux côtés opposés ( médiane, voir plus bas ).
Un polygone isocèle qui présente plusieurs axes-miroir a nécessairement un centre, le point d'intersection des axes-miroir.
Quelques exemples et contre-exemples :
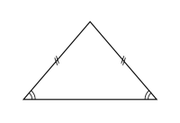
- le triangle isocèle, qui a deux côtés égaux, présente un axe-miroir passant par le sommet commun aux deux côtés égaux et le milieu du côté opposé ;
- les quadrilatères isocèles convexes sont :
-
-
- le trapèze isocèle ; il a deux côtés parallèles, et présente un axe-miroir passant par les milieux de ces deux côtés ;
- le cerf-volant est aussi un polygone isocèle ; il présente un axe-miroir passant par deux sommets opposés, et ses diagonales sont perpendiculaires ;
- le losange peut être vu comme un cas particulier de cerf-volant qui présente deux axes-miroirs passant par ses paires de sommets opposés, et confondus avec ses diagonales ;
-
- tout polygone régulier est isocèle et présente autant d'axes-miroir que de côtés ;
- le parallélogramme n'est pas isocèle (sauf s'il s'agit d'un losange).
Polygone centrosymétrique
Un polygone est dit centrosymétrique quand il présente un centre de symétrie.
Tout polygone centrosymétrique a nécessairement un nombre pair de sommets, et inversement, seuls les polygones d'ordre pair peuvent être centrosymétriques.
Les côtés opposés d'un polygone centrosymétrique sont parallèles et de même longueur (ordre du polygone pair).
Polygone centrosymétrique (parallélogramme).Quelques exemples et contre-exemples :
- les triangles ne peuvent pas avoir de centre de symétrie ;
- les quadrilatères centrosymétriques sont les parallélogrammes (côtés opposés parallèles et de même longueur) ;
- les seuls quadrilatères présentant à la fois un centre de symétrie et un axe-miroir sont les rectangles et les losanges ;
- tout polygone régulier d'ordre pair a un centre de symétrie.
Polygone rotosymétrique
Un polygone est dit rotosymétrique d'ordre n ou plus brièvement n-rotosymétrique quand il présente un axe de rotation d'ordre n.
Un polygone rotosymétrique d'ordre n a un nombre de côtés multiple de n. Inversement, un polygone ne peut présenter d'axe de rotation que si l'ordre de ce dernier divise son nombre de côtés.
Les polygones réguliers et centrosymétriques sont des cas particuliers de polygones rotosymétriques.
Quelques exemples et contre-exemples :
- un triangle ne peut présenter d'axe de rotation que s'il est d'ordre 3 ; il est alors régulier, donc équilatéral ;
- tout quadrilatère rotosymétrique est centrosymétrique ;
- le cas le plus simple de polygone rotosymétrique sans être centrosymétrique ou régulier est celui de l'hexagone 3-rotosymétrique ;
- tout polygone régulier présente par définition un axe de rotation du même ordre que le polygone ;
- tout polygone convexe d'ordre premier présentant un axe de rotation est régulier.
Polygone scalène (triangle scalène).Polygone scalène
Un polygone scalène est un polygone qui ne présente aucun élément de symétrie. Un polygone scalène n'a donc pas de centre de symétrie.
Classement par les angles
Un polygone convexe ne peut présenter plus de quatre angles droits.
Polygone rectangle
Un polygone est dit rectangle quand il comporte au moins un angle droit.
Quelques exemples et contre-exemples :
- un triangle rectangle comporte un angle droit et deux angles aigus ;
- un quadrilatère rectangle comporte au moins un angle droit ; ce n'est cependant pas forcément un rectangle, qui en comporte quatre ;
- dès qu'un trapèze comporte un angle droit, c'est un trapèze rectangle ; mais tout trapèze rectangle comporte forcément au moins deux angles droits adjacents ;
- le seul polygone régulier rectangle est le carré. C'est d'ailleurs un cas particulier de rectangle, avec quatre angles droits.
Polygone birectangle
Un polygone est dit birectangle quand il comporte au moins deux angles droits, consécutifs ou non.
Quelques exemples et contre-exemples :
- aucun triangle n'est birectangle, du moins en géométrie euclidienne (il existe des triangles birectangles, et même trirectangles, sur une sphère) ;
- les quadrilatères convexes birectangles sont :
-
-
- les trapèzes rectangles, qui présentent deux angles droits consécutifs ;
- les semi-rectangles, qui présentent deux angles droits non consécutifs ; on peut les décrire comme deux triangles rectangles accolés par leur hypoténuse ;
-
- le seul trapèze semi-rectangle est le rectangle ;
- le seul polygone régulier birectangle est le carré.
Un polygone avec deux angles droits consécutifs présente deux côtés parallèles.
Polygone trirectangle
Un polygone est dit trirectangle quand il comporte au moins trois angles droits, consécutifs ou non.
Quelques exemples et contre-exemples :
- aucun triangle n'est trirectangle ;
- les seuls quadrilatères convexes trirectangles sont les rectangles, qui comptent d'ailleurs quatre angles droits ;
- le seul polygone régulier trirectangle est le carré.
Un polygone convexe avec trois angles droits consécutifs présente deux fois deux côtés parallèles. Il ressemble en fait à un rectangle avec un coin découpé.
Polygone équiangle
Un polygone est dit équiangle quand tous ses angles sont égaux.
Quelques exemples et contre-exemples :
- le seul triangle équiangle est le triangle équilatéral ;
- les quadrilatères convexes équiangles sont les rectangles ;
- tous les polygones réguliers sont équiangles.
Autres classements
Polygone équilatéral
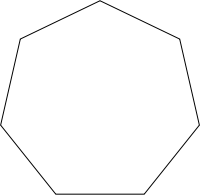Polygone équilatéral (heptagone régulier).Un polygone est dit équilatéral quand tous ses côtés ont la même longueur.
Quelques exemples et contre-exemples :
- les quadrilatères convexes équilatéraux sont les losanges ;
- tous les polygones réguliers sont équilatéraux.
Polygone inscriptible (dans un cercle)
Un polygone est dit inscriptible quand tous ses sommets se trouvent sur un même cercle, dit circonscrit au polygone. Ses côtés sont alors des cordes de ce cercle, d'où le nom de polygone de cordes donné par les anglophones aux polygones inscriptibles.
Quelques exemples et contre-exemples :
- tout triangle est inscriptible ;
- un trapèze n'est inscriptible que s'il est isocèle ;
- tout semi-rectangle est inscriptible ;
- le seul parallélogramme inscriptible est le rectangle ;
- tout polygone régulier est inscriptible.
Polygone circonscriptible (à un cercle)
Un polygone est dit circonscriptible quand tous ses côtés sont tangents à un même cercle, dit inscrit dans le polygone. Les anglophones ont baptisés polygone de tangentes ce type de polygone.
Quelques exemples et contre-exemples :
- tout triangle est circonscriptible ;
- les seuls parallélogrammes circonscriptibles sont les losanges ;
- tout polygone régulier est circonscriptible.
Autres définitions et propriétés
Médiatrices d'un polygone
Ce sont les médiatrices de ses côtés.
Bissectrices d'un polygone
Ce sont les bissectrices de ses angles.
Médianes et diagonales principales d'un polygone
- Si l'ordre n du polygone est pair :
-
-
- on appelle diagonale principale de ce polygone tout segment reliant deux sommets opposés. Ces diagonales principales sont au nombre de
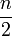. Si le polygone est régulier, ses diagonales principales sont aussi appelées diamètres, car elles sont alors aussi des diamètres du cercle circonscrit au polygone. - on appelle médiane de ce polygone tout segment reliant les milieux de deux côtés opposés. Ces médianes sont aussi au nombre de .
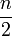- on appelle diagonale principale de ce polygone tout segment reliant deux sommets opposés. Ces diagonales principales sont au nombre de
-
- Si l'ordre du polygone est impair, il n'y a pas de diagonales principales, seulement des médianes. Chaque médiane relie alors un sommet au milieu du côté opposé. Elles sont alors au nombre de
.
Apothèmes et rayons d'un polygone à centre
Apothéme d'un hexagone.Les apothèmes d'un polygone à centre relient les milieux de ses côtés à son centre.
Si le polygone est régulier, ce sont aussi :
- les demi-médianes du polygone, s'il est d'ordre pair ;
- les lignes de construction définissant les médiatrices de ses côtés ;
- des rayons du cercle inscrit dans le polygone.
Les rayons d'un polygone à centre relient ses sommets à son centre.
Si le polygone est régulier, ce sont aussi :
- les demi-diamètres du polygone, s'il est d'ordre pair ;
- des rayons du cercle circonscrit au polygone.
Notion d'angle au centre
Soit A1A2A3...An un polygone à n côtés muni d'un centre O.
On appelle angle au centre du polygone l'angle
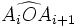formé par deux rayons consécutifs de ce polygone.Si le polygone considéré est régulier, les n angles au centre ont tous la même mesure, 2π / n radians, et c'est aussi la mesure de l'angle entre deux apothèmes consécutifs.
Somme des angles (ou Théorème de Santarelli)
La somme des angles d'un polygone ne porte pas de nom particulier, mais vaut (seulement dans le cas d'un polygone convexe ) :
, 
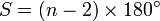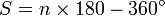ou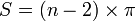 
radians, où n est l'ordre du polygone.
DémonstrationPour le démontrer, prenez un point à l'intérieur du polygone ; reliez-y tous les sommets, vous obtenez alors un découpage du polygone en n triangles ; sachant que la somme des angles d'un triangle vaut π radians, celle des n triangles vaut donc n·π radians ; en y soustrayant la somme des angles autour du point central commun aux n triangles, qui vaut 2 π radians, la somme des angles vaut donc S = n·π - 2·π. En factorisant par π, on obtient le résultat cité plus haut : S = (n - 2)·π radians.
À noter que lorsque l'ordre d'un polygone augmente d'une unité, la somme de ses angles augmente de 180° ou π radians : c'est le supplément d'angle.
Périmètre d'un polygone (Théorême de Viet)
Le périmètre d'un polygone est la somme des longueurs de ses côtés.
Si le polygone est régulier, son périmètre P vaut :
où :
- n est l'ordre du polygone ;
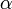est son angle au centre ;- et R le rayon du cercle qui lui est circonscrit.
Comme
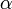vaut 2π / n radians, et que sin x ≈ x quand x est voisin de 0, le périmètre tend vers 2 π R quand n tend vers l'infini. On retrouve bien le périmètre du cercle.Aire d'un polygone (Lemme de Boursier)
L'aire d'un polygone non croisé est l'aire de la surface enclose par le polygone.
Si le polygone est régulier, son aire A vaut :
où :
- n est l'ordre du polygone ;
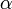- est son angle au centre ;
- et R le rayon du cercle qui lui est circonscrit.
Comme l'angle au centre vaut 2 π / n radians, et que sin x ≈ x et cos x ≈ 1 quand x est voisin de 0, l'aire tend vers π R2 quand n tend vers l'infini. On retrouve bien l'aire du disque.
Il existe une seconde formule possible pour calculer l'aire d'un polygone régulier :
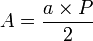
où a est l'apothème du polygone et P son périmètre.
Lorsque le polygone est irrégulier, il est facile de le partitionner en triangles à partir des diagonales. Pour calculer son aire, il suffit alors de faire la somme des aires des triangles obtenus.
Voir aussi
Articles connexes
- Calcul du centre de gravité d'un polygone
- Construction à la règle et au compas
- Partage d'une tarte
- Théorème de Gauss-Wantzel
- Simplification d'un polygone
- Forme cristalline
- Polyèdre
- Polytope
- Polygone de sustentation
Liens externes
- Quelques informations sur les polygones
- De nombreuses informations complémentaires sur les polygones
Références
- ↑ En géométrie sphérique, on peut le représenter par un sommet placé sur un grand cercle.
- ↑ a et b Dans ses Méditations Métaphysiques, Descartes se sert du chiliogone et du myriogone pour montrer la différence entre l'imagination et la conception pure.
Portail de la géométrie
Catégorie : Polygone
Wikimedia Foundation. 2010.
