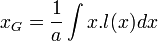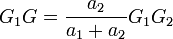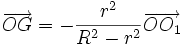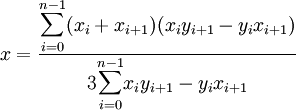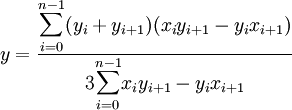Calcul du centre de gravité d'un polygone

Centre de gravité d'une plaque homogène

En mécanique, le centre de gravité d'une plaque homogène est le point par rapport auquel la masse est uniformément répartie. Pratiquement, c'est le centre d'équilibre de la plaque. On dit qu'une plaque est homogène lorsque elle a "la même poids partout" c'est-à-dire lorsque sa densité est constante.

Le centre de gravité d'une plaque homogène peut se calculer à l'aide du calcul intégral mais il existe des règles simples qui permettent de trouver directement le centre de gravité de plaques dont la forme géométrique est remarquable en utilisant l'outil géométrique du barycentre.

Sommaire

1 Principes
2 Calcul intégral
3 Constructions de centres de gravité et formulaire
- 3.1 Mise en pratique des principes
- 3.2 Formulaire
4 Annexes

Principes

Centre de gravité d'un triangle

Si la plaque homogène a la forme d'un triangle, son centre de gravité correspond à l'intersection des médianes. C'est donc aussi l'isobarycentre des sommets. Cette situation est assez singulière pour être signalée. En général, le centre de gravité d'une plaque homogène polygonale ne coïncide pas avec l'isobarycentre de ses sommets.

Éléments de symétrie

Si la plaque homogène possède un axe de symétrie alors le centre de gravité est situé sur cet axe.

Si la plaque homogène est invariante par rotation d'angle non trivial, son centre de gravité est confondu avec son centre de rotation. En particulier, si la plaque homogène possède un centre de symétrie c'est aussi son centre de gravité.

Le centre de gravité d'un parallélogramme est donc l'intersection de ses diagonales. Le centre de gravité d'un cercle ou d'un ellipse coïncide avec leur centre.

Principe d'addition et de soustraction

Une plaque homogène composée de deux plaques $P 1$ et $P 2$ de centre de gravité $G 1$ et $G 2$ a pour centre de gravité le barycentre des points $G 1$ et $G 2$ pondérés par les surfaces des plaques $P 1$ et $P 2$ .

Une plaque homogène composée d'une plaque P, de centre de gravité G et d'aire a, de laquelle a été ôtée une plaque $P 1$ de centre de gravité $G 1$ et d'aire $a 1$ a pour centre de gravité le barycentre des point G et $G 1$ pondérés par les réels a et - $a 1$ .

Le centre de gravité d'une plaque polygonale peut donc être déterminée en découpant le polygone en triangles, en construisant le centre de gravité $G i$ de chaque triangle et en calculant chacune de leurs aires $a i$ , le centre de gravité est alors le barycentre du système pondéré ${G i, a i)}$ . On verra dans les exemples que l'on peut même se passer du calcul des aires en utilisant des propriétés d'alignement.

Calcul intégral

Si l'on munit la plaque d'un repère orthonormé, l'abscisse et l'ordonnée du centre de gravité peuvent être calculées à l'aide d'un calcul intégral. Si l'on appelle l(x) la longueur totale de la section de la plaque par la droite d'abscisse x, et si a est l'aire de la plaque, l'abscisse du centre de gravité est donné par la formule

$x_G = \frac 1a \int x.l(x)dx$

Constructions de centres de gravité et formulaire

Mise en pratique des principes

Centre de gravité d'une plaque en forme de L

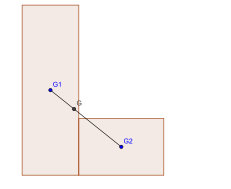
La plaque en forme de L est formée de deux rectangles de centres $G 1$ et $G 2$ et d'aire $a 1$ et $a 2$ . Le centre de gravité de la plaque est donc le barycentre de ${(G 1, a 1)(G 2, a 2)}$ , il est situé entre $G 1$ et $G 2$ et vérifie :

$G_1G = \frac{a_2}{a_1+a_2}G_1G_2$

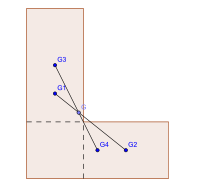
Dans le dessin ci-dessous, le petit rectangle est deux fois plus petit que le grand, la distance $G 1 G$ est donc égale au tiers de la distance $G 1 G 2$ . On remarque que le point G est aligné avec $G 1$ et $G 2$ . Cette propriété permet d'éviter le calcul des aires : il suffit d'imaginer deux découpages différents de la plaque. Le point G étant situé sur sur la droite ( $G 1 G 2$ ) et sur la droite ( $G 3 G 4$ ), il correspond alors au point d'intersection de ces deux droites. Cela est facilement réalisable pour la plaque en L car elle peut être découpée en deux rectangles de deux manières différentes.

Centre de gravité d'une plaque en forme de quadrilatère

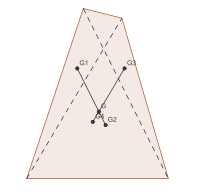
La plaque peut être découpée suivant une diagonale en deux triangles dont les centre de gravité $G 1$ et $G 2$ sont aisés à construire. Le centre de gravité de la plaque est alors aligné avec ces deux points.

Un autre découpage de la plaque suivant l'autre diagonale fournit un autre alignement.

Le centre de gravité est alors le point d'intersection des droites ( $G 1 G 2$ ) et ( $G 3 G 4$ ). On remarque que ce point ne coïncide pas avec l'isobarycentre des sommets qui serait le milieu des milieux des diagonales.

Centre de gravité d'un torque

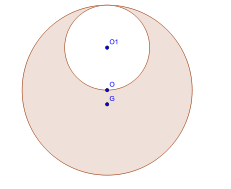
Un torque est constitué d'un cercle de centre O de rayon R dans lequel a été découpé un cercle de centre $O 1$ de rayon r tangent au premier cercle. Les surfaces des plaques sont proportionnelles au carré des rayons. Le centre de gravité du torque est alors le barycentre du système ${(O, R 2),(O 1, - r 2)}$ . On a donc

$\overrightarrow{OG}=-\frac{r^2}{R^2-r^2}\overrightarrow{OO_1}$

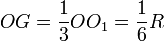Dans le dessin ci-contre, le rayon du petit cercle est deux fois plus petit que le rayon du grand, les points $O 1$ , O et G sont alignés dans cet ordre et $OG=\frac 13 OO_1 = \frac 16 R$ .

Formulaire

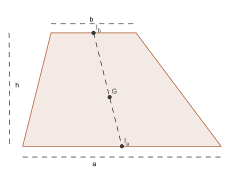
Trapèze

Le centre de gravité d'un trapèze de bases a > b et de hauteur h est situé sur la médiane joignant les deux bases et à une distance de la grande base égale à 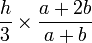$\frac h3\times\frac{a+2b}{a+b}$ . C'est le barycentre des milieux

I a

I b

des deux bases affectés des coefficients 2a + b et 2b + a.

Polygone

Si le polygone a pour sommets les points $A 0, A 1,... A n = A 0$ , si $A i$ a pour coordonnées $(x i, y i)$ alors les coordonnées de G sont données par les formules

$x=\frac{\displaystyle{\sum_{i=0}^{n-1}}(x_i+x_{i+1})(x_iy_{i+1}-y_ix_{i+1})}{3\displaystyle{\sum_{i=0}^{n-1}}x_iy_{i+1}-y_ix_{i+1}}$

$y=\frac{\displaystyle{\sum_{i=0}^{n-1}}(y_i+y_{i+1})(x_iy_{i+1}-y_ix_{i+1})}{3\displaystyle{\sum_{i=0}^{n-1}}x_iy_{i+1}-y_ix_{i+1}}$

Cette formule est valable pour un polygone sans trou et non croisé ^[1]

Secteur circulaire

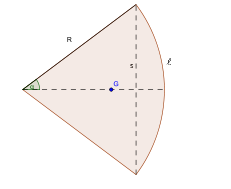
Le centre de gravité d'un secteur circulaire d'angle 2

α

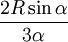(en radian) et de rayon R est situé sur la bissectrice de l'angle et à une distance du centre égale à $\frac{2R\sin\alpha}{3\alpha}$ .

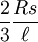
Si l'on note s la corde et $\ell$ l'arc du secteur angulaire, le centre de gravité est à une distance du centre égale à $\frac 23 \dfrac{Rs}{\ell}$

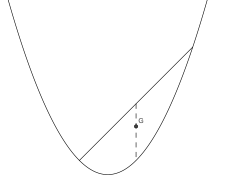
Parabole

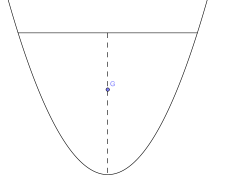
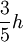
Le centre de gravité d'un plaque en forme de parabole de hauteur h est sur l'axe de symétrie de la parabole et à une distance du sommet égale à $\frac 35 h$

De manière plus générale, le centre de gravité d'une section de parabole est située au 3/5 de la flèche en partant du sommet.

Annexes

Notes et références

↑ (en) polygon area and centroid

Bibliographie

Gieck, Formulaire technique

Voir aussi

Ce document provient de « Centre de gravit%C3%A9 d%27une plaque homog%C3%A8ne ».

Catégories : Géométrie affine | Mécanique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Calcul du centre de gravité d'un polygone de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Calcul Du Centre De Gravité D'un Polygone — Centre de gravité d une plaque homogène En mécanique, le centre de gravité d une plaque homogène est le point par rapport auquel la masse est uniformément répartie. Pratiquement, c est le centre d équilibre de la plaque. On dit qu une plaque est… … Wikipédia en Français
Calcul du centre de gravite d'un polygone — Centre de gravité d une plaque homogène En mécanique, le centre de gravité d une plaque homogène est le point par rapport auquel la masse est uniformément répartie. Pratiquement, c est le centre d équilibre de la plaque. On dit qu une plaque est… … Wikipédia en Français
Centre de gravité — Pour la notion de centre de gravité en géométrie, voir Centre de gravité d un polygone. En physique, le centre de gravité (CdG), appelé G, est le point d application de la résultante des forces de gravité ou de pesanteur. Il est également le… … Wikipédia en Français
Centre de gravité d'une plaque homogène — En mécanique, le centre de gravité d une plaque homogène est le point par rapport auquel la masse est uniformément répartie. Pratiquement, c est le centre d équilibre de la plaque. On dit qu une plaque est homogène lorsque elle a la même poids… … Wikipédia en Français
Calcul de l'aire d'un polygone — Polygone Pour les articles homonymes, voir Polygone (homonymie). En géométrie euclidienne, un polygone (du grec polus, nombreux, et gônia, angle) est une figure géométrique plane, formée d une suite de segments, chacun d entre eux partageant une… … Wikipédia en Français
Aire et centre de masse d'un polygone — En géométrie, l aire d un polygone est la mesure de la superficie de la région délimitée par le polygone. En mécanique, le centre de masse d un polygone, interprété comme centre de masse d une plaque homogène polygonale, est le point autour… … Wikipédia en Français
Centre de masse d'une plaque homogène — En mécanique, le centre de masse d une plaque homogène est le point par rapport auquel la masse est uniformément répartie. Pratiquement, dans le cas d un champ de pesanteur uniforme le centre de masse est confondu avec le centre de gravité de la… … Wikipédia en Français
CALCUL INFINITÉSIMAL - Histoire — L’expression «calcul infinitésimal» désigne habituellement l’ensemble des notations et des méthodes fondamentales du calcul différentiel, du calcul intégral et du calcul des variations, tel qu’il a été mis au point au cours des XVIIe et XVIIIe… … Encyclopédie Universelle
Hectagone — Polygone Pour les articles homonymes, voir Polygone (homonymie). En géométrie euclidienne, un polygone (du grec polus, nombreux, et gônia, angle) est une figure géométrique plane, formée d une suite de segments, chacun d entre eux partageant une… … Wikipédia en Français
Polygonale — Polygone Pour les articles homonymes, voir Polygone (homonymie). En géométrie euclidienne, un polygone (du grec polus, nombreux, et gônia, angle) est une figure géométrique plane, formée d une suite de segments, chacun d entre eux partageant une… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Calcul du centre de gravité d'un polygone

Centre de gravité d'une plaque homogène

Sommaire

Principes

Centre de gravité d'un triangle

Éléments de symétrie

Principe d'addition et de soustraction

Calcul intégral

Constructions de centres de gravité et formulaire

Mise en pratique des principes

Centre de gravité d'une plaque en forme de L

Centre de gravité d'une plaque en forme de quadrilatère

Centre de gravité d'un torque

Formulaire

Annexes

Notes et références

Bibliographie

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Calcul du centre de gravité d'un polygone

Centre de gravité d'une plaque homogène

Sommaire

Principes

Centre de gravité d'un triangle

Éléments de symétrie

Principe d'addition et de soustraction

Calcul intégral

Constructions de centres de gravité et formulaire

Mise en pratique des principes

Centre de gravité d'une plaque en forme de L

Centre de gravité d'une plaque en forme de quadrilatère

Centre de gravité d'un torque

Formulaire

Annexes

Notes et références

Bibliographie

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link