Théorème flot-max/coupe-min

Théorème flot-max/coupe-min

Théorème flot-max/coupe-min

Le théorème flot-max/coupe-min est un théorème de la théorie des graphes. Il généralise le théorème de König et le théorème de Hall (dans les graphes bipartis) et le théorème de Menger (dans les graphes quelconques). Il révèle que le calcul d'une coupe minimum peut se ramener à un problème de flot maximum.

Énoncé

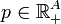Soit G = (V,A) un graphe orienté avec une pondération positive de ses arcs p\in \R_+^A.

Une coupe de G est un sous-ensemble d'arcs D qui possède la propriété suivante:

Il existe une partition des sommets du graphes en deux sous-ensembles S et T tels que D est l'ensemble de tous les arcs dont l'extrémité initiale est dans S et l'extrémité terminale dans T.

Une coupe sépare un sommet s de t, si s est dans S tandis que t est dans T. La capacité d'une coupe est la somme des pondérations de ses arcs.

Un flot dans G est un vecteur 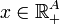x\in \R_+^A satisfaisant la loi des noeuds des lois de Kirchhoff en tout sommet de G sauf deux. On peut supposer que pour l'un de ces sommets, l'origine s, aucun flot ne rentre, tandis que pour l'autre, la destination du flot t, aucun flot ne sort. La valeur d'un flot est la somme totale du flot sortant de s (valant celle du flot rentrant dans t par la conservation de flot découlant des lois de Kirchhoff).

Théorème flot-max/coupe-min (indépendamment P. Elias, A. Feinstein et C.E. Shannon, et L.R. Ford, Jr. et D.R. Fulkerson, 1956) — Pour tout graphe, tout couple (s,t) de sommets du graphe, et pour toute pondération positive, la valeur maximum du flot de s à t est égale à la capacité minimum d'une coupe séparant s de t.

Ce théorème s'étend aux graphes non orientés.

Généralisation des théorèmes de König, Hall et Menger

Il est clair que Menger est un cas particulier du théorème flot-max/coupe-min. Pour voir que ce théorème permet d'obtenir les deux théorèmes sur les graphes bipartis, il faut associer à un graphe biparti G = (A,B;E) le graphe orienté D obtenu en ajoutant un sommet source s et des arcs de s vers les sommets de A et en ajoutant un sommet puis t et des arcs des sommets de B vers t, et en orientant les arêtes de G dans le sens A vers B. Pour König, le couplage min de G correspond clairement au flot max dans D si tous les arcs ont une capacité 1. 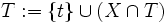La coupe min (S,T) séparant s et t de D s'obtient à partir d'un transversal T de G en définissant S:= \{s\} \cup (Y\cap T) et T:= \{t\} \cup (X\cap T) , et vice-versa. Pour Hall, il suffit de remarquer que pour tout 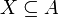X \subseteq A on a que 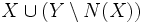X\cup (Y\setminus N(X)) est un transversal de G. Donc la cardinalité d'un transversal min (et donc d'une coupe min) par le raisonnement précédent a pour cardinalité 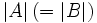|A|\, (=|B|) si et seulement si la condition de Hall est vérifiée.

Ce document provient de « Th%C3%A9or%C3%A8me flot-max/coupe-min ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème flot-max/coupe-min de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Theoreme flot-max/coupe-min — Théorème flot max/coupe min Le théorème flot max/coupe min est un théorème de la théorie des graphes. Il généralise le théorème de König et le théorème de Hall (dans les graphes bipartis) et le théorème de Menger (dans les graphes quelconques).… …   Wikipédia en Français

  • Theoreme de Konig (theorie des graphes) — Théorème de König (théorie des graphes) En théorie des graphes, un couplage d un graphe G est un sous ensemble d arêtes de G deux à deux non adjacentes. Un transversal de G est un sous ensemble de sommets T de G avec la propriété que toute arête… …   Wikipédia en Français

  • Théorème de könig (théorie des graphes) — En théorie des graphes, un couplage d un graphe G est un sous ensemble d arêtes de G deux à deux non adjacentes. Un transversal de G est un sous ensemble de sommets T de G avec la propriété que toute arête de G est incidente à au moins un sommet… …   Wikipédia en Français

  • Théoreme de Hall — Théorème de Hall Le théorème de Hall donne une condition nécessaire et suffisante à l existence d un couplage parfait dans un graphe biparti (un couplage parfait dans un graphe ayant un nombre pair 2n de sommets est un sous ensemble de n arêtes… …   Wikipédia en Français

  • Théorème de hall — Le théorème de Hall donne une condition nécessaire et suffisante à l existence d un couplage parfait dans un graphe biparti (un couplage parfait dans un graphe ayant un nombre pair 2n de sommets est un sous ensemble de n arêtes deux à deux… …   Wikipédia en Français

  • Theoreme de Menger — Théorème de Menger En théorie des graphes, le théorème de Menger est à l origine du théorème flot max/coupe min qui le généralise. Il fut prouvé par Karl Menger en 1927. Le théorème de Menger s énonce ainsi : le nombre minimum d arêtes dont… …   Wikipédia en Français

  • Théorème de menger — En théorie des graphes, le théorème de Menger est à l origine du théorème flot max/coupe min qui le généralise. Il fut prouvé par Karl Menger en 1927. Le théorème de Menger s énonce ainsi : le nombre minimum d arêtes dont la suppression… …   Wikipédia en Français

  • Flot admissible — Problème de flot maximum Un exemple de graphe de flot avec un flot maximum. la source est s, et le puits t. Les nombres indiquent le flot et la capacite. Le problème de flot maximum consiste a trouver un flot réalisable depuis une source unique… …   Wikipédia en Français

  • Théorème de König (théorie des graphes) — Pour les articles homonymes, voir Théorème de König. En théorie des graphes, un couplage d un graphe G est un sous ensemble d arêtes de G deux à deux non adjacentes. Un transversal de G est un sous ensemble de sommets T de G avec la propriété que …   Wikipédia en Français

  • Théorème de Hall —  Ne pas confondre avec le théorème de Hall en théorie des groupes, ni avec le problème des ménages. En mathématiques, le théorème de Hall ou lemme des mariages est un résultat combinatoire qui donne une condition nécessaire et suffisante,… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”