Nomogramme

Un nomogramme est un outil graphique de calcul constitué de courbes graduées entre lesquelles on place une règle. Le résultat de l'opération se lit au croisement de la règle et de l'une des courbes représentées en rouge dans les exemples ci-dessous. Le terme a été créé par Maurice d'Ocagne qui fut le principal promoteur de cette technique au début du XX^e siècle.

Exemple

La parabole à faire des multiplications

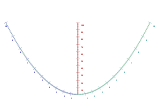
La parabole que voici est doublement cotée, ce qui veut dire qu'en fait on considère comme séparées les deux moitiés de celle-ci, graduées respectivement en bleu et en cyan. L'axe de la parabole, en rouge, est également gradué, mais les graduations ne vont plus jusqu'à 10 comme sur les deux branches latérales, mais jusqu'à 100.

Utilisation de la parabole pour effectuer le produit de 6 par 8 (ou le quotient de 48 par 6)

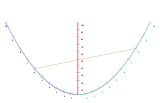
Pour effectuer le produit de 6 par 8, il suffit de tirer un trait (ou pour conserver longtemps le nomogramme, poser une règle ou tendre un fil) entre la graduation 6 de la branche bleue et la graduation 8 de la branche cyan. Ci-contre le trait est en marron, et on voit qu'il coupe l'axe rouge sur la graduation 48, ce qui confirme que  : Cette parabole est en fait une machine à multiplier. Promue comme telle par Clark, elle semble inspirée par des recherches de paraboles dans la table de multiplication par August Ferdinand Möbius en 1841^[1].

On peut manipuler ce nomogramme en ligne ici: [2].

Remarque historique

Plusieurs auteurs récents^[2],[3] attribuent ce procédé de calcul à Yuri Matiyasevich, ce qui est impossible du point de vue de la chronologie (Matiyasevich a publié la recette du nomogramme en 1971^[4]). Il est très possible qu'à l'époque il ait ignoré les travaux de Clark, vu le peu de renommée de ceux-ci.

Multiplication

En fait, l'utilisation de deux courbes pour les deux opérandes et une troisième pour le résultat peut se généraliser à toutes les opérations de deux variables du type z = x^αy^β, il suffit pour cela de graduer les deux courbes bleue et cyan selon x^α et y^β respectivement. Ce qui permet, entre autres, de calculer la puissance électrique dans une résistance P = RI², l'énergie donnée par la masse par la relation d'Einstein E=mc², la loi de Snell etc.

Il est d'ailleurs parfaitement possible d'effectuer des divisions avec le nomogramme ci-dessus, en permutant les rôles des points d'intersection.

Les exemples ci-dessous montrent donc tous des multiplications.

Autres exemples

Nomogramme à droites parallèles

Le nomogramme à droites parallèles, historiquement le premier du genre

Le premier nomogramme publié par Maurice d'Ocagne^[5] est formé de droites parallèles.

Le principe de son utilisation est simple: On repère sur les droites extrêmes les deux facteurs à multiplier (graduations respectivement bleue et cyan) et on tire entre les deux, un trait rectiligne (de préférence matérialisé sous forme d'une règle ou d'un fil tendu pour ne pas laisser de marque sur le nomogramme).

Les graduations utilisent une échelle logarithmique et le principe du nomogramme est basé sur la conservation du milieu par projection.

On peut manipuler ce nomogramme en ligne ici: [3].

Nomogrammes de Clark

En 1907 et 1908, J. Clark, de l'école polytechnique du Caire, publia^[6] une série d'articles où il expose l'utilisation par ses collègues de nomogrammes nouveaux. Il ébauche une théorie unificatrice de ces nomogrammes, qui utilisent des cubiques. En particulier, comme la parabole unie à son axe est une courbe cubique, la théorie de Clark explique le fonctionnement du nomogramme parabolique. Il l'étend à l'utilisation d'autres coniques.

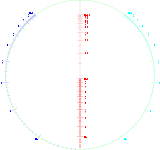
Nomogramme circulaire

Le nomogramme circulaire de Clark, un cercle uni à un de ses diamètres.

Le cercle est une conique, ce qui donne lieu à ce nomogramme de multiplication. Comme précédemment, les facteurs se lisent sur les graduations bleue et cyan, entre lesquelles on trace (virtuellement) un trait, et on lit le produit sur la graduation rouge qui est alignée avec ces deux graduations.

On peut manipuler ce nomogramme en ligne ici: [4].

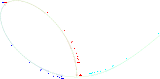
Folium

Le nomogramme de Clark est un simple folium, triplement coté.

Le folium est aussi une courbe cubique, ce qui a permis à Clark de construire une courbe à multiplier unique, où la même courbe porte les graduations des facteurs et celles du produit. Ce nomogramme fut présenté au congrès de Cherbourg en 1905, où il bénéficia d'un franc succès.

On peut manipuler ce nomogramme en ligne ici: [5].

Abaques

Il est constitué d’un réseau de courbes correspondant chacune à un paramètre et permettant de trouver une valeur numérique sans calcul explicite mais graphiquement. Par exemple :

• la règle à calcul
• les abaques professionnels : Ce sont des graphiques à lecture directe facilitant les calculs numériques. - Graphiques servant à déterminer spontanément des résultats obtenus par des calculs dans un système de lignes prédéfinies et préparées d’avance. Le nom actuel serait nomogramme au sens étymologique du mot (de nomos : loi, division). Constitué sur la base de graphiques à échelles diverses établis par le tracé de nombre de droites, souvent parallèles, rarement concourantes. Les abaques s’exploitent par une lecture directe, sans avoir à effectuer de tracés complémentaires soit en lisant directement les données se situant à l’intersection des droites correspondante par la lecture du point concourant en relation avec les besoins de l’intervenant.
  • abaque de Smith pour les calculs de câbles électriques
  • abaque de Black dans le plan de Nichols en automatique
  • abaque des marées au service hydrologique et océanographique de la marine
  • abaque de dépouillement, de Hull et Davay en cristallographie
  • abaque de lecture en microbiologie pour la constitution d’antibiogrammes
  • abaque de magnitude en sismologie
  • abaque de conversion franc/euros, Celsius/Fahrenheit
  • abaque d'Heldio Lenz César en cartographie pour traiter le problème de la variation de surface d'un figuré ponctuel ou d'une forme géométrique
  • Nomogramme de Henssge en médecine légale pour la datation des cadavres

Notes et références

Annexes

Articles connexes

• Règle à calcul
• Astrolabe
• Logarithme
• Conique
• Cercle
• Folium
• Unicursale
• Abaque de Smith

Liens externes

• Une utilisation pédagogique de la parabole de Möbius en classe de 3^e
• Rubrique de l'IREM de la Réunion sur les nomogrammes, avec des nomogrammes en ligne; il y a aussi d'autres nomogrammes, notamment pour la résolution des équations du second degré
• Une étude de cas, où on calcule graphiquement un indice de masse corporelle; la moitié des outils sont des nomogrammes

• Portail de la géométrie