Puissance (physique)

Pour les articles homonymes, voir Puissance.

En physique, la puissance est la quantité d'énergie par unité de temps fournie par un système à un autre. La puissance correspond donc à un débit d'énergie : deux systèmes de puissances différentes pourront fournir le même travail (la même énergie), mais le système le plus puissant sera le plus rapide.

Généralités

Dans certains cas, il faut une grande puissance au démarrage (grande énergie sur une courte durée), donc seuls les systèmes puissants peuvent faire fonctionner le dispositif. C'est notamment le cas lorsqu'il faut vaincre un frottement sec ou bien lorsqu'il y a un effet de seuil (comme par exemple la vitesse minimale de décollage d'un avion ou d'une fusée). Une rame de métro nécessite une puissance d'environ 1 mégawatt pour se lancer, et 10 à 15 fois moins pour maintenir sa vitesse de croisière.

La puissance est toujours égale au produit d'une grandeur d'effort (force, couple, pression, tension, etc.) par une grandeur de flux (vitesse, vitesse angulaire, débit, intensité du courant, etc.)

L'unité de puissance du SI est le watt, abrégée W, qui correspond à un joule fourni par seconde.

On utilise encore le cheval-vapeur dans le cas des moteurs thermiques :

1 ch = 736 W environ.

Toujours dans le domaine automobile, la puissance fiscale, est un paramètre arbitraire défini par l'administration. En France, depuis juillet 1998, la puissance fiscale dépend de la valeur normalisée d'émission de dioxyde de carbone (CO₂) en g/km et de la puissance maximale du moteur en kW. Si on note C la quantité de CO₂ rejetée (en g/km) et P la puissance du moteur (en kW), alors :

$\mathrm{P_{CV}} = \frac{\mathrm{C}}{45} + (\frac{\mathrm{P}}{40})^{1,6}$

La puissance moyenne P_m est l'énergie E délivrée par un phénomène divisée par la durée τ de ce phénomène :

$\mathrm{P_m} = \frac{\mathrm{E}}{\tau}$

La puissance instantanée est la dérivée de l'énergie fournie par rapport au temps :

$\mathrm{P} = \frac{\mathrm{dE}}{\mathrm{d}t}$

et l'on a :

$\mathrm{P_m} = \frac{1}{\tau} \int_0^\tau \mathrm{P}(t) \cdot \mathrm{d}t$

Par abus de langage, on attribue la puissance à l'objet qui la transforme, par exemple :

un moteur de 100 ch ;
une lampe de 100 W.

Dans ce cas il s'agit :

soit de la puissance maximale (moteur à plein régime, ou à régime donné) ;
soit de la puissance nominale sous condition de fonctionnement (par exemple lampe alimentée en 230 V).

En mécanique

Puissance d'une force

Si le point d'application d'une force $\vec{\mathrm{F}}$ (en N) se déplace à la vitesse instantanée $\vec{v}$ (en m/s), alors la puissance instantanée vaut (en W)

$\mathrm{P} = \vec{\mathrm{F}} \cdot \vec{v}$

On retrouve aisément ce résultat en dérivant le travail d'une force.

Puissance d'un couple.

Si l'objet est en rotation sous l'action d'un couple $\vec{\mathrm{C}}$ (en N·m) et tourne à la vitesse angulaire instantanée $\vec{\Omega}$ (en rad/s), alors la puissance instantanée vaut (en W)

$\mathrm{P} = \vec{\mathrm{C}} \cdot \vec{\Omega}$ .

Puissance des interactions.

Dans une liaison parfaite, la puissance des interactions est nulle. On obtient cette grandeur par le calcul du co-moment des torseurs cinématique et statique de la liaison.

Puissance des torseurs

Article détaillé : Torseur – Puissance générale.

Principe des puissances virtuelles

Article détaillé : Principe des puissances virtuelles.

C'est un principe fondamental en mécanique, il met sous forme variationnelle les équations traditionnelles de la mécanique. Il permet aussi d'établir des relations entre les puissances extérieures d'un mécanisme (et donc d'obtenir des lois entrée/sortie par exemple).

En électricité

Cas général : régimes variables

Si la tension et le courant varient, la puissance instantanée consommée par un dipôle est égale au produit des valeurs instantanées du courant qui le traverse et de la tension à ses bornes.

$p(t) = u(t) \cdot i(t) \,$

avec p en watts, u en volts et i en ampères.

Puissance en continu

En régime de tension et de courant continu,

$P = U \cdot I \,$

$U \,$ et $I \,$ étant les valeurs constantes de la tension aux bornes du dipôle et de l'intensité du courant à travers le dipôle.

Puissance dissipée par une résistance : effet Joule

Si $R \,$ est la résistance du dipôle, alors on a :

$U = R \cdot I \,$

Cela conduit à l'expression de la puissance :

$P = R \cdot I^2 = \frac{U^2}{R} \,$

Puissance dissipée par un dipôle actif linéaire

Bilan de puissance avec la convention "générateur"

D'un point de vue électrique, on peut modéliser un dipôle actif linéaire (électromoteur) par un Modèle équivalent de Thévenin (M.E.T.). Remarque : ce modèle est très sommaire et ne rend compte que de la chute de tension en charge ou des puissances électriques mises en jeu que dans un domaine de validité qui devrait toujours être précisé. En convention générateur (flèche de tension et sens du courant dans le même sens), le schéma équivalent du dipôle est donc le suivant: Met1-electric energy.png

En convention générateur, la puissance fournie par le dipôle à l'extérieur s'écrit par définition :

$P_{fournie} = U \cdot I = (E-r \cdot I) \cdot I = E \cdot I - r \cdot I^2 \,$

La puissance fournie $P_{fournie} \,$ par le dipôle actif correspond donc à la puissance fournie par un générateur idéal de tension $E \,$ délivrant un courant $I \,$ dont une partie est dissipée par effet Joule $- r \cdot I^2 \,$

Dans le cas des moteurs électriques le terme $E \cdot I \,$ est appelé puissance électromécanique souvent noté $P_{em} \,$

Bilan de puissance avec la convention "récepteur"

Si l'on choisit la convention récepteur pour décrire le dipole, le schéma est identique à celui présenté au paragraphe précédent, à la seule différence que la tension u est orientée dans le sens opposé (la fléche de tension et le sens du courant sont ne sont pas dans le même sens). Bilan des puissances électriques (approximatif, déduit d'un modèle):

La puissance dissipée par le dipôle est fournie par l'alimentation électrique (non représentée sur le schéma) :

P_dissipée = U⋅I.

Cette puissance est transformée en puissance électromagnétique P_em et en pertes par effet Joule p_J :

P_dissipée ≃ P_em + p_J

U⋅I = = (-E + r⋅I)⋅I= -E⋅I + r⋅I².

Rendement

Le rendement η (êta, sans dimension) est défini par $\eta =\frac{\mathrm{P_u}}{\mathrm{P_a}}$ Dans le cas où le dipôle actif fonctionne en récepteur :

$\eta = \frac{\mathrm{P_{em}}}{\mathrm{U}\cdot \mathrm{I}} = \frac{\mathrm{E}}{\mathrm{U}}$

Dans le cas où le dipôle actif fonctionne en générateur

$\eta = \frac{\mathrm{U}\cdot \mathrm{I}}{\mathrm{P_{em}}}= \frac{\mathrm{U}}{\mathrm{E}}$

On a toujours η < 1.

Puissances en régime sinusoïdal de tension et de courant

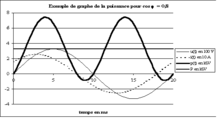La courbe ci-dessus représente la puissance consommée par un dipôle soumis à une tension sinusoïdale de valeur efficace égale à 230 V, traversé par un courant également sinusoïdal de valeur efficace égale à 18 A et dont le facteur de puissance est égal à 0,8. On constate que la puissance instantanée varie entre +7,45 kW et -0,83 kW soit une amplitude de variation de 8,3 kW (2UI) et une moyenne d'environ 3,3 kW : = UI cos φ.

En régime sinusoïdal, le courant et la tension ont pour expression :

$i(t) = i_0 \cdot \cos(\omega t ) = \mathrm{I} \sqrt 2 \cdot \cos(\omega t ) \,$

$u(t) = u_0 \cdot \cos (\omega t + \varphi ) = \mathrm{U} \sqrt 2 \cdot \cos (\omega t+ \varphi ) \,$

où U et I sont les valeurs efficaces de la tension et du courant, et φ est le déphasage de la tension par rapport au courant.

Le produit de ces deux grandeurs a pour expression :

$p(t) = \mathrm{U}\mathrm{I} \cdot \cos(\varphi) + \mathrm{U}\mathrm{I} \cdot \cos(2 \omega t + \varphi ) \,$

Le premier terme de la somme est appelé puissance active, le deuxième terme de la somme puissance fluctuante. Cette somme correspond à une puissance sinusoïdale de fréquence double de celle du courant et de la tension et dont la position moyenne est égale à la puissance active.

La valeur de cos(φ) correspond au facteur de puissance en régime sinusoïdal.

Puissance active

Article détaillé : Puissance active.

La puissance moyenne consommée en régime sinusoïdal porte le nom de puissance active. Cette dénomination provient de la méthode de Boucherot (voir ci-dessous).

Elle a pour expression :

$\mathrm{P} = \mathrm{U} \cdot \mathrm{I} \cdot \cos \varphi = \frac{u_0 \cdot i_0}{2}\cdot \cos \varphi \,$

(U et I sont des valeurs efficaces)

Puissance fluctuante

C'est une puissance sinusoïdale de fréquence double de celle du courant et de la tension. C'est elle qui impose une distribution en triphasé des fortes puissances.

Puissance apparente et réactive — Théorème de Boucherot

Articles détaillés : Puissance apparente et Puissance réactive.

Le théorème de Boucherot permet, en régime sinusoïdal de tension et de courant, de calculer la puissance totale consommée par une installation électrique comportant plusieurs dipôles de facteur de puissance divers, ainsi que le courant total appelé dans cette installation. Cette méthode permet de faire des calculs selon un formalisme de type vectoriel sans utiliser la représentation de Fresnel plus lourde lorsque l'on est en présence de nombreux dipôles.

Pour appliquer cette méthode, il est nécessaire de créer deux intermédiaires de calcul qui n'ont pas véritablement de sens physique :

la puissance apparente notée S est égale au produit des valeurs efficaces :
S = U⋅I
en volt-ampère (VA) ;
La puissance réactive notée Q, est telle que
Q = U⋅I⋅sin φ
en volt-ampère réactif (var).

Les unités sont différentes des watts alors qu'elles sont homogènes à une puissance, afin de respecter le principe physique qui autorise d'additionner des grandeurs de mêmes unités. En effet, additionner des puissances actives avec des puissances réactives ou apparentes n'a aucun sens physique.

Les trois « puissances » sont liées par la relation :

S² = P² + Q².

Soit un dipôle dont l'impédance complexe s'écrit : Z = R + jX. On a :

P = R⋅I² ;
Q = X⋅I² ;
S = |Z|⋅I².

De plus on a par définition :

$\cos \varphi = \frac{\mathrm{P}}{\mathrm{S}}$

$\sin \varphi = \frac{\mathrm{Q}}{\mathrm{S}}$

donc

$\tan \varphi = \frac{\mathrm{Q}}{\mathrm{P}}$ .

Puissance complexe

La puissance complexe est un outil mathématique de traitement des puissances électriques à l'aide de la transformation complexe.

S = U⋅I^*,
où I^* est le nombre complexe conjugué de l'intensité complexe I (les modules de U et I sont des valeurs efficaces) ;
S = P + jQ,
avec P : puissance active et Q : puissance réactive.

Puissance en régime triphasé

Article détaillé : Triphasé.

Puissances en régime sinusoïdal de tension et en régime non sinusoïdal de courant

Ce cas est très important : La distribution de l'électricité se fait en régime sinusoïdal de tension (si l'on fait abstraction de la pollution du réseau), mais une grande quantité des récepteurs utilisés par les particuliers ou les industriels appellent des courants non-sinusoïdaux du fait des convertisseurs de l'électronique de puissance qui sont utilisés pour les alimenter. En particulier, la majorité des appareils électroniques grand-public sont alimentés à travers un montage redresseur qui absorbe un courant alternatif en forme de pics.

Expression de la puissance

Dans l'expression générale de la puissance :

p(t) = u(t)⋅i(t)

on substitue la décomposition en séries de Fourier de chacune des grandeurs :

u(t) étant supposée sinusoïdale, elle ne contient qu'un seul harmonique de valeur efficace U₁ = U ;
$i(t) = \mathrm{I}_1 \sqrt 2 \cos( \omega t + \varphi_1) + \dots + \mathrm{I}_n \sqrt 2 \cos (n \omega t + \varphi_n)\,$ .

Seul les produits de termes de même fréquence ont une valeur moyenne non nulle. La puissance active est donc :

$\mathrm{P} = \mathrm{U}_1 \cdot \mathrm{I}_1 \cdot \cos \varphi_1 \,$

Seul le premier harmonique (le fondamental) transporte la puissance active.

Puissance thermique

La puissance thermique est une notion attachée au flux thermique (ou flux de chaleur) à travers une surface. Cette notion de conduction thermique est expliquée dans les articles Conduction thermique et transfert thermique. Dans ces articles, on introduit de manière unidimensionnelle la densité de flux thermique :

$\varphi= - \lambda \frac{\delta \mathrm{T}}{\delta x}\,$ .

Pour généraliser cette densité de flux dans toutes les directions (y et z), on définit le vecteur densité de flux thermique suivant : $\vec{\mathcal{J}}_\mathrm{Q} = - \lambda^*\overrightarrow{\mathrm{grad}}(\mathrm{T})$ (loi de Fourier).

Cette expression de la propagation de chaleur présente 2 avantages :

elle est tridimensionnelle (elle exprime la propagation dans toutes les directions de l'espace)
on peut librement utiliser les coordonnées de notre choix (cartésiennes, cylindriques ou sphériques)

Le choix des coordonnées dépend de la symétrie du problème. Par exemple, si on étudie la chaleur produite par un fusible (cylindrique), on utilisera bien sûr les coordonnées cylindriques.

La puissance thermique à travers une surface S (noté $\mathcal{P}_\mathrm{Q}$ ), par définition, est le flux du vecteur $\vec{\mathcal{J}_\mathrm{Q}}$ à travers la surface S, c'est-à-dire :

$\mathcal{P}_\mathrm{Q} = \iint\limits_\mathrm{S} \vec{\mathcal{J}}_\mathrm{Q} \vec \mathrm{dS}$

Remarques

Les systèmes de coordonnées sont détaillés dans l'article suivant : Système de coordonnées.
La surface S peut être ouverte ou fermée. La différence entre une surface fermée et une surface ouverte est expliquée dans l'article : Surface.

Notes et références

Liens externes

Site offrant une explication ludique des notions de puissance et de couple moteur

Portail de l’électricité et de l’électronique
Portail de la physique

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Puissance (physique) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Puissance efficace — Puissance apparente La puissance apparente est définie comme étant la valeur maximale de la puissance active[1],[2]. On a donc la puissance apparente Pap : où p(t) est la puissance instantanée. La puissance apparente se … Wikipédia en Français
Puissance apparente — La puissance apparente est définie comme étant la valeur maximale qui peut être prise par la puissance active[1],[2] pour des amplitudes de tension et d intensité fixées. Le rapport de la puissance active sur la puissance apparente est appelé… … Wikipédia en Français
Puissance active — La puissance active (ou puissance moyenne) est la moyenne temporelle de la puissance instantanée[1],[2]. On a donc pour un système en évolution périodique de période temporelle T la puissance active : où p( … Wikipédia en Français
puissance — [ pɥisɑ̃s ] n. f. • 1150; de puissant I ♦ (Sens faible) 1 ♦ Vx Puissance de... : moyen ou droit grâce auquel on peut (faire qqch.). ⇒ capacité. « La puissance de bien juger [...] est égale en tous les hommes » (Descartes). 2 ♦ Mod. Philos.… … Encyclopédie Universelle
Puissance en regime alternatif — Puissance en régime alternatif Diagramme complexe de la puissance en régime alternatif : Puiss. réelle (P, en Watt (W)) Puiss. réactive (Q, en voltampère réactif (VAr)) Puiss. complexe (S, en voltampère (VA)) Puiss. apparente (abs(S), en… … Wikipédia en Français
Puissance réactive — Puissance en régime alternatif Diagramme complexe de la puissance en régime alternatif : Puiss. réelle (P, en Watt (W)) Puiss. réactive (Q, en voltampère réactif (VAr)) Puiss. complexe (S, en voltampère (VA)) Puiss. apparente (abs(S), en… … Wikipédia en Français
Physique, Chimie, Sciences de l'Ingénieur — Dans le système éducatif français, physique, chimie et sciences de l ingénieur ou PCSI est une des voie d orientation en Classe préparatoire aux grandes écoles scientifiques. Il s agit de l une des 3 grandes filières en première année (Maths Sup) … Wikipédia en Français
Physique, Chimie et Sciences de l'Ingénieur — Physique, chimie, sciences de l ingénieur Dans le système éducatif français, physique, chimie et sciences de l ingénieur ou PCSI est une des voie d orientation en Classe préparatoire aux grandes écoles scientifiques. Il s agit de l une des 3… … Wikipédia en Français
Physique, chimie, sciences de l'ingenieur — Physique, chimie, sciences de l ingénieur Dans le système éducatif français, physique, chimie et sciences de l ingénieur ou PCSI est une des voie d orientation en Classe préparatoire aux grandes écoles scientifiques. Il s agit de l une des 3… … Wikipédia en Français
Physique, chimie, sciences de l'ingénieur — Dans le système éducatif français, physique, chimie et sciences de l ingénieur ou PCSI est une des voie d orientation en Classe préparatoire aux grandes écoles scientifiques. Il s agit de l une des 3 grandes filières en première année (Maths Sup) … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Puissance (physique)

Sommaire

Généralités