- Cône (topologie)
-
Pour les articles homonymes, voir Cône.
Cône d'un cercle. L'espace original est en bleu, et l'extrémité réduite à un point est en gris.
En topologie, et en particulier en topologie algébrique, le cône CX d'un espace topologique X est l'espace quotient:
du produit de X par l'intervalle unité I = [0, 1]. Intuitivement nous transformons X en un cylindre et on réduit une extrémité du cylindre à un point.
Si X appartient à un espace euclidien, le cône construit sur X est homéomorphe à l'union des droites allant des points de X à un autre point. C'est-à-dire que le cône topologique coïncide avec le cône géométrique bien défini. Cependant, la construction du cône topologique est plus générale.
Exemples
- Le cône construit sur un point p de la droite réelle est l'intervalle {p} x [0,1].
- Le cône construit sur deux points {0,1} est un "V" avec les extrémités en {0} et {1}.
- Le cône construit sur un intervalle I de la droite réelle est un triangle plein, aussi appelé 2-simplexe (voir l'exemple final).
- Le cône construit sur un polygone P est une pyramide de base P.
- Le cône construit sur un disque est le solide cône de la géométrie classique (d'où le nom de ce concept).
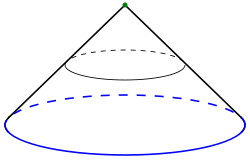
- Le cône construit sur un cercle est la surface courbe du cône solide:
-
- Ce dernier est homéomorphe au disque fermé.
- Plus généralement le cône construit sur une n-sphère est homéomorphe à la (n+1)-boule fermée.
- Le cône construit un n-simplexe est un (n+1)-simplexe.
Propriétés
Tous les cônes sont connexes par arcs puisque tout point peut être relié au sommet. De plus, tout cône est contractile, c'est-à-dire qu'il est homotopiquement équivalent à un point à savoir son sommet par l'homotopie
- ht(x,s) = (x, (1−t)s).
Le cône est utilisé en topologie algébrique précisément parce qu'il transforme un espace en un sous-espace d'un espace contractile. Mais l'inclusion de l'espace à la base du cône est une cofibration, ce qui permet de définir la cofibre homotopique de l'écrasement d'un espace sur un point comme sa suspension.
Lorsque X est compact et séparé (essentiellement, lorsque X peut être plongé dans l'espace euclidien), alors le cône CX peut être visualisé comme la réunion des segments joignant tout point de X à un point unique. Cependant, cette image ne fonctionne plus si X n'est pas compact ou séparé, car généralement la topologie quotient sur CX est plus fine que la topologie de la réunion des segments joignant X à un point.
Foncteur Cône
L'application
induit un foncteur 
sur la catégorie des espaces topologiques Top.
Wikimedia Foundation. 2010.
