Ératosthène

Cet article concerne un savant grec du III^e siècle avant notre ère . Pour Ératosthène, un des trente oligarques s'étant emparés du pouvoir à Athènes après la guerre du Péloponnèse, voir Les Trente.

Ératosthène
Naissance	-276 Cyrène Libye
Décès	-194 Alexandrie Égypte
Champ(s)	Astronomie, géographie, mathématiques, philosophie
Célèbre pour	Catalogue d'étoiles, Crible d'Ératosthène, Duplication du cube, Sphère armillaire

Ératosthène (en grec ancien Ἐρατοσθένης / Eratosthénês) était un astronome, géographe, philosophe et mathématicien grec du III^e siècle avant notre ère (né à Cyrène, aujourd'hui Shahat en Libye, v. -276 ; mort à Alexandrie, Égypte, v. -194). Il fut l'élève d'Ariston de Chios.

Ératosthène fut nommé à la tête de la bibliothèque d'Alexandrie^[1] vers -245^[2] à la demande de Ptolémée III, pharaon d'Égypte, et fut précepteur de son fils Ptolémée IV^[3].

Selon Suidas, il se laissa mourir de faim, parce que, devenu aveugle, il ne pouvait plus admirer les étoiles^[4].

Il est célèbre pour être le premier dont la méthode de mesure de la circonférence de la Terre soit connue.

On a donné son nom à l'astéroïde (3251) Ératosthène^[5].

Travaux

Mathématiques

En tant que mathématicien, il établit le crible d'Ératosthène, méthode qui permet de déterminer par exclusion tous les nombres premiers. Il travailla sur le problème de la duplication du cube, et imagina le mésolabe, instrument propre à connaître les moyennes proportionnelles^[6],[7].

Astronomie

En tant qu'astronome, il mit au point des tables d'éclipses et un catalogue astronomique de 675 étoiles. Il démontra l'inclinaison de l'écliptique^[8] sur l'équateur et fixa cette inclinaison à 23°51 (la valeur correcte est 23°26 en moyenne). Il inventa la sphère armillaire^[9].

Histoire

En histoire, il continua les recherches de Manéthon sur l'Égypte antique, et dressa une chronologie des rois thébains.

Géographie et géométrie

Ses études portaient sur la répartition des océans et des continents, les vents, les zones climatiques et les altitudes des montagnes. On lui attribue le terme géographie. Il laissa une carte générale de l'écoumène qui fut longtemps l'unique base de la géographie : il y donnait la valeur de 47°42' à l'arc du méridien compris entre les deux tropiques ; vingt siècles après lui, l'Académie française des sciences retrouvait à peu près la même mesure (47°40').

C'est cependant l'étude de la circonférence de la Terre qui marque le plus les travaux d'Ératosthène.

Mesure de la circonférence de la Terre

On attribue en général l'idée de la sphéricité de la Terre à l'école pythagoricienne ou au Parménide dès le VI^e siècle. La Terre était déjà considérée comme sphérique par Platon (V^e siècle) et par Aristote (IV^e siècle)^[10]. La plus ancienne mesure de la Terre qui nous soit connue est rapportée par Aristote^[11] et s'élève à 400 000 stades.

La méthode utilisée par Ératosthène est décrite par Cléomède dans sa Théorie circulaire des corps célestes.

Ératosthène déduisit la circonférence de la Terre^[12],[13] (ou méridien terrestre) d'une manière purement géométrique.

Il compara l'observation qu'il fit sur l'ombre de deux objets situés en deux lieux, Syène (aujourd'hui Assouan) et Alexandrie, considérés situés sur le même méridien, le 21 juin (solstice d'été) au midi solaire local. C'est à ce moment précis de l'année que dans l'hémisphère nord le Soleil détient la plus haute position au-dessus de l'horizon. Or, dans une précédente observation, Ératosthène avait remarqué qu'il n'y avait aucune ombre dans un puits à Syène (ville située à peu près sur le tropique du Cancer) ; ainsi, à ce moment précis, le Soleil était à la verticale et sa lumière éclairait directement le fond du puits. Ératosthène remarqua cependant que le même jour à la même heure, un obélisque situé à Alexandrie formait une ombre ; le Soleil n'était donc plus à la verticale et l'obélisque avait une ombre décentrée. Ératosthène considérait parallèles les rayons lumineux du Soleil en tout point de la terre. Il en déduisit que l'angle entre les rayons solaires et la verticale était de 7,2 degrés.

Ératosthène évalua ensuite la distance entre Syène et Alexandrie en faisant appel à un bématiste qui se basa sur le temps en journées de marche de chameau entre les deux villes : la distance obtenue était de 5 000 stades, soit 787,5 km, mesure très proche de la réalité, un stade égyptien valant environ 157,5 m.

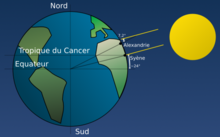Calcul de la circonférence de la Terre.

Par la théorie géométrique des angles alternes-internes congrus, Ératosthène proposa une figure d'une éblouissante simplicité : elle était composée d'un simple cercle ayant un angle au centre de 7,2 degrés qui intercepte un arc (reliant Syène à Alexandrie) de 800 km. Par les rapports dans les cercles (déjà connus à l'époque), il calcula que la circonférence de la Terre était de :

• 5 000 stades de 157,5 m valent 787,5 km (et forment un angle de 7,2°) ;
• 360° : 7,2° = 50 arcs de 7,2° ;
• 787,5 km x 50 = 39 375 km (soit 250 000 stades), mesure remarquablement précise pour l'époque (les mesures actuelles donnent 40 075,02 km^[14])^[15].

Bibliographie

Ouvrages d'Ératosthène

Il avait composé une Description de la Grèce, un précis des Conquêtes d'Alexandre, et avait même écrit sur la comédie attique.

Malheureusement il ne reste de lui que quelques fragments, édités en grec :

– avec une trad. en latin par Günther Karl Friedrich Seidel, Eratosthenis Geographicorum fragmenta, Göttingen, 1798 (en ligne) ;

– et d'une manière plus complète par Gottfried Bernhardy, Eratosthenica, Berlin, 1822 (en ligne).

• Sur la mesure de la Terre :

– Cléomède, Théorie élémentaire (De motu circulari corporum caelestium), trad. par Richard Goulet, Paris, 1980 (Histoire des doctrines de l’Antiquité classique) (en ligne) ; compte rendu par Maurice Caveing, dans Revue d'histoire des sciences, 35-2, 1982 p. 165-167.

• Géographie :

– A. Thalamas, La Géographie d'Ératosthène, Paris, 1921.

– Eratosthenes' Geography. Fragments collected and translated, éd. grecque et trad. angl. par Duane W. Roller, Princeton et Oxford, 2010 (ISBN 978-0-691-14267-8) (présentation).

• Constellations (Catastérismes) ^[16]

Études sur Ératosthène

• Germaine Aujac, Ératosthène de Cyrène, le pionnier de la géographie : sa mesure de la circonférence terrestre, Paris, 2001 (Format, 39) (ISBN 2-7355-0457-3).
• Germaine Aujac, La Géographie dans le Monde antique, Paris, 1975, p. 15-20 et 70-78 (à propos de la géographie et de la carte d'Ératosthène) ("Que sais-je ?", 1598).
• C. Cusset et H. Frangoulis (dir.), Ératosthène, un athlète du savoir, Publications de Saint-Étienne, 2008
• P. Dépech, La géographie des Grecs, PUF, 1976.
• Pierre Duhem, Le système du monde, histoires des doctrines cosmologiques de platon à Copernic, 10 vol., Hermann, Paris (1913—1959), T.II, chap. IX.
• Marie-Nicolas Bouillet et Alexis Chassang (dir.), « Ératosthène » dans Dictionnaire universel d’histoire et de géographie, 1878  (Wikisource)

Romans

• Denis Guedj, Les Cheveux de Bérénice, Seuil, 2003.
• Jean Romain, Le Bibliothécaire, Éditions L'Âge d'Homme, 2005.

Voir aussi

Articles connexes

• catastérisation
• Crible d'Ératosthène
• Les représentations du monde avant les grandes découvertes
• Lagynophoria
• Archimède
• Al-Biruni

Liens externes

 Ératosthène sur Commons

• Schémas sur la mesure de la circonférence de la Terre
• Ératosthène, l'Arpenteur de la Terre : animation pédagogique (histoire des sciences, calcul de la circonférence de la Terre, angles alternes/internes)
• Le crible d'Ératosthène
• La mesure de la Terre par Ératosthène : Cet article écrit par Arkan Simaan pour Futura-Sciences revient sur la question de la précision de la mesure d’Ératosthène.
• Le gnomon d'Eratosthène (animation GeoGebra)

Notes et références

• Portail de la philosophie antique
• Portail de la philosophie
• Portail de l’astronomie
• Portail de la géographie
• Portail des mathématiques
• Portail de la Grèce antique