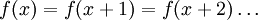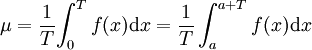- Fonction Périodique
-
Fonction périodique
 Pour les articles homonymes, voir Période.
Pour les articles homonymes, voir Période.En mathématiques, une fonction périodique est une fonction qui lorsqu'elle est appliquée à une variable, reprend la même valeur si on ajoute à cette variable une certaine quantité fixe appelée période. Des exemples de telles fonctions peuvent être obtenus à partir de phénomènes périodiques, comme l'heure indiquée par la petite aiguille d'une horloge, les phases de la lune, etc.
Sommaire
Définition
Une fonction f définie sur un ensemble
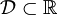 de nombres réels est dite périodique de période
de nombres réels est dite périodique de période 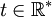 (ou t-périodique) si et seulement si:
(ou t-périodique) si et seulement si:Pour une fonction périodique, le graphe peut être tracé en recopiant de façon répétitive, une portion particulière de longueur une période, à intervalles réguliers : c'est une propriété d'invariance par translation.
Par exemple, la fonction partie fractionnaire f qui associe à un nombre réel sa partie fractionnaire définie par
Ici, [x] désigne la partie entière de x. La fonction f est périodique et de période 1. Ainsi nous avons
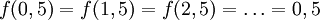 .
.
Si une fonction f est périodique de période t alors pour tout x appartenant à l'ensemble de définition de f et pour tout entier n:
- f(x + nt) = f(x)
Ce résultat se démontre par récurrence.
Dans l'exemple précédent, la fonction étant de période 1, nous avons pour tout réel x
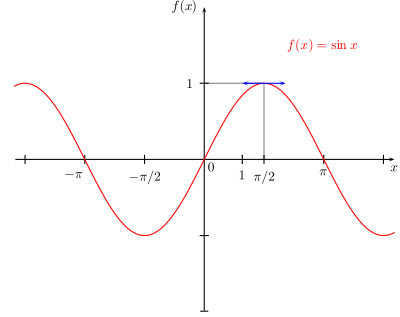
Si on considère l'ensemble des périodes strictement positives d'une fonction f et si f est continue et que cet ensemble n'admet pas de plus petit élément alors f est constante, sinon f admet une plus petite période strictement positive. Les fonctions sinus et cosinus sont périodiques et de période 2π.
La théorie des séries de Fourier cherche à écrire une fonction périodique arbitraire comme une somme de fonctions trigonométriques.
En physique, un mouvement périodique est un mouvement dans lequel la position, (ou les positions) d'un système sont exprimables à l'aide de fonctions périodiques du temps, ayant toute la même période. Voyez par exemple les articles onde en dent de scie, et onde triangulaire
Moyenne, dérivée et primitive des fonctions périodiques numériques
Valeur moyenne
La valeur moyenne d'une fonction périodique f intégrable de période T est la valeur suivante, qui est indépendante de a :
Ainsi la fonction cosinus est de moyenne nulle, son carré de moyenne 1/2.
Quitte à ajouter une constante à la fonction, on peut changer sa valeur moyenne.
Dérivée et primitive
- La dérivée d'une fonction
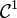 , T-périodique, est T-périodique et de moyenne nulle
, T-périodique, est T-périodique et de moyenne nulle - Une fonction f continue et T-périodique admet une primitive T-périodique si et seulement si f est de moyenne nulle (toutes les primitives sont alors périodiques, une seule étant de moyenne nulle).
Pour une étude plus précise des propriétés de la dérivation pour les fonctions périodiques, il faut introduire les séries de Fourier ; on peut alors démontrer l'inégalité de Wirtinger qui compare les normes de f et de sa dérivée.
Définition plus générale et ensemble de périodes [réf. souhaitée]
Soient E un ensemble muni d'une loi de composition interne notée additivement + et F un ensemble quelconque. Un élément
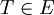 étant donné, une fonction T-périodique ou fonction de période T de E dans F, est une fonction de E dans F telle que:
étant donné, une fonction T-périodique ou fonction de période T de E dans F, est une fonction de E dans F telle que: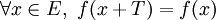 .
.
Remarquons qu'à moins que la loi soit supposée commutative cette définition dépend de la place de T à droite.
Plus fréquemment, E est un groupe commutatif dont l'ensemble des périodes possibles forme un sous-groupe.
Une fonction dont l'ensemble de définition est l'ensemble des nombres complexes peut avoir deux périodes incommensurables sans être constante. Les fonctions elliptiques vérifient cette propriété (incommensurable veut dire dans ce contexte qu'elles ne sont pas multiples par un réel l'une pour l'autre.)Voir également
- Portail des mathématiques
Catégories : Analyse réelle | Analyse harmonique
Wikimedia Foundation. 2010.

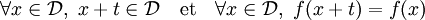
![\forall x\in\mathbb{R},\ f(x)=x-[x]](/pictures/frwiki/97/ac7da331269a91a12abad3a6a74894b7.png)