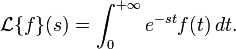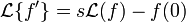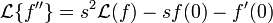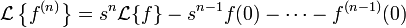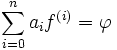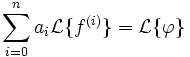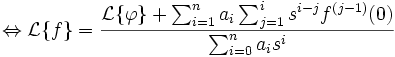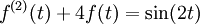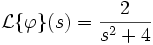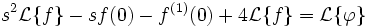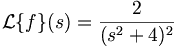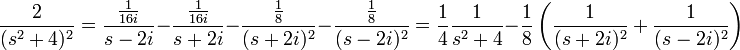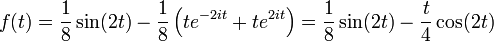- Application De La Transformée De Laplace Aux Équations Différentielles
-
Application de la transformée de Laplace aux équations différentielles
Dans la résolution des équations différentielles linéaires à coefficients constants, les propriétés de de la transformation de Laplace, concernant la linéarité et la transformée de la dérivée, offrent un moyen de résoudre certaines d'entre elles. Cette technique est un outil pratique pour les ingénieurs.Principe
La transformation de Laplace transforme une fonction
 en une fonction
en une fonction 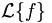 définie par
définie parEn pratique, la recherche de
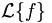 se fait plus facilement à l'aide de tables de transformées de Laplace (voir quelques transformées usuelles)
se fait plus facilement à l'aide de tables de transformées de Laplace (voir quelques transformées usuelles)La transformation de Laplace possède les propriétés suivantes
Linéarité :
- :
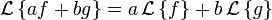
Transformée d'une dérivée :
Ces propriétés peuvent s'appliquer à une équation différentielle linéaire. Supposons que l'on veuille résoudre l'équation différentielle suivante :
En appliquant la transformation de Laplace à cette égalité on obtient l'équation équivalente suivante :
où
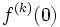 sont les conditions initiales.
sont les conditions initiales.Il suffit alors de trouver
 en appliquant la transformation inverse sur
en appliquant la transformation inverse sur 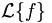 . Cette opération se révèle parfois difficile sauf dans le cas où
. Cette opération se révèle parfois difficile sauf dans le cas où 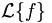 est une somme de transformées de Laplace classiques figurant dans un tableau de transformées de Laplace.
est une somme de transformées de Laplace classiques figurant dans un tableau de transformées de Laplace.Un exemple
On cherche à résoudre :
avec les conditions initiales
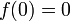 et
et 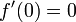
On note :
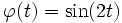
Le tableau de transformées de Laplace donne :
L'équation devient :
On en déduit :
Il s'agit maintenant de retrouver la fonction
 , c'est à dire d'appliquer la transformation de Laplace inverse. Dans ce cas, la fonction
, c'est à dire d'appliquer la transformation de Laplace inverse. Dans ce cas, la fonction 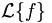 est une fonction rationnelle qu'il suffit de décomposer en éléments simples. La lecture inverse du tableau de transformées de Laplace fournira alors la valeur de
est une fonction rationnelle qu'il suffit de décomposer en éléments simples. La lecture inverse du tableau de transformées de Laplace fournira alors la valeur de 
Toutes ces différentes fractions figurent dans la colonne de droite du tableau de transformées de Laplace et permettent de retrouver
 :
:- Portail des mathématiques
Catégories : Article à désacadémiser | Analyse fonctionnelle | Équation différentielle
Wikimedia Foundation. 2010.