- Calcul opérationnel
-
Le calcul opérationnel repose essentiellement sur un astucieux changement de variable basé sur la Transformée de Laplace permettant l'algébrisation des symboles de dérivation et d'intégration des expressions mathématiques décrivant les phénomènes linéaires. Les ingénieurs emploient de préférence la transformation de « Laplace-Carson », une constante ayant comme image la même constante.
L'expression :
permet d'associer à toute fonction d'une variable 
dite « fonction origine » une « fonction image » 
. Ainsi la solution algébrique de l'équation image pemet de retrouver, au moyen d'un tableau de correspondance opératoire, la solution de l'équation origine.La transformation directe est notée :
image de 
La transformation inverse est notée :
- original de
Sommaire
Transformations de base
Pour une constante « C »
La correspondance entre fonctions originales et fonctions images s'établit comme suit :
est l'original de ,
est l'original de 
,
est l'original de 
,
est l'original de 
.
Image d'une variable « t »
Pour
, on obtient l'image 
Ainsi,
-
est l'original de
-
est l'original de 
-
est l'original de 
D'une manière générale, par récurrence pour tout « n » entier positif, on obtient :
original de 
Image de l'exponentielle de « at »
Si
, la parenthèse devient :![[e^{(\alpha-p)t}(cos \beta t + i sin \beta t]_0^{+\infty}
\,](b/66b6f11b71c650f0f54321afeb3db0fb.png)
, expression qui tend vers 
lorsque que 
, dans ce cas l'image de 
est 
Pour « a » réel, le tableau de correspondance opératoire s'établit comme suit :Fonction origine Fonction image Fonction origine Fonction image Condition(s) 
- 
Pour
Fonction origine Fonction image Fonction origine Fonction image Condition(s) 
- 
- 
- - -
Si, l'image de 
est : 
Fonction origine Fonction image Fonction origine Fonction image Condition(s) 
- Si
, la valeur de est égale à zéro pour 
, idem pour la valeur de la fonction image lorsque 
.Hypothèse fondamentale
L'hypothèse fondamentale du calcul opérationnel est que toutes fonctions d'origines f(t) ont une valeur nulle pour toute valeur de « t » négative. Bien que négligé la plupart du temps dans la pratique, il convient cependant d'écrire les fonctions d'origines comme facteur de la fonction U(t), dite fonction échelon-unité. Exemple : la forme d'origine de
est 
Représentation de U(t).eat.
L'échelon unité
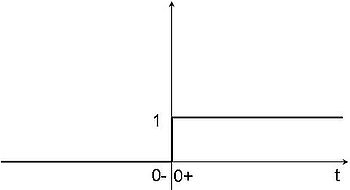
La fonction U(t) échelon-unité est nulle pour toute valeur négative de « t » et égale à 1 pour toute valeur positive de « t ». Elle est représentée ci-dessous. Son symbole est la lettre grecque Upsilon majuscule et se lit « grand upsilon » de t. Elle se caractérise par son brusque passage de 0 à 1 entre 0- et 0+. Elle admet partout une dérivée nulle sauf en zéro où elle devient infinie.
Représentation de la fonction échelon-unité U(t).Introduction à la fonction de Dirac (percussion-unité)
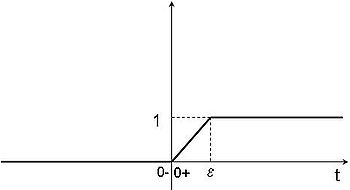
Considérons une fonction h(t) telle que représentée ci-dessous. Elle est définie par :
pour 
,
pour 
,
pour 
.
Représentation de la fonction
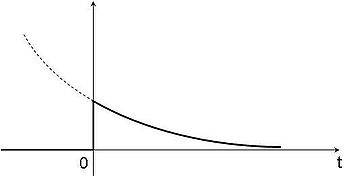
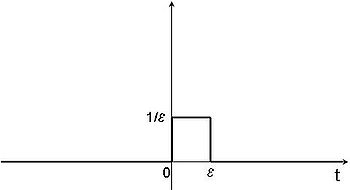
.La fonction h(t) a pour dérivée g(t), représentée ci-dessous, caractérisée par :
pour ,
pour ,
- pour .
Quel que soit
, l'aire du rectangle est égal à l'unité.
Représentation de la fonction
.Fonction de Dirac ou percussion-unité
Si l'on fait tendre
vers zéro, tend vers 
et 
tend vers une fonction notée 
qui est notre fonction de Dirac (ou percussion-unité) caractérisée par deux valeurs :*
quel que soit « t » sauf pour 
où la valeur de devient infinie, et
*
, quel que soit t0 ≤ 0 et t > 0.
Il vient alors :
Image de l'impulsion de Dirac
L'image de l'impulsion de Dirac est la limite quand
tend vers zéro de l'expression maintenant bien connue :
Ce qui est égal à
qui, quand tend vers zéro (règle de l'Hospital, par ex.), est égale à 1.
L'image de l'impulsion de Dirac d(t) est donc 1.Transformation des dérivées
En dérivant une fonction d'origine :
![f^'(t).U(t) = [f(t).U(t)]^'-f(0)U^'(t) \,](6/056c71ec21c886272637bef6a5461ae6.png)
,
On trouve la dérivée de la fonction d'origine :![[f(t).U(t)]^' = f^'(t)U(t)+f(0)u^'(t) \,](9/ca9cc9c735378726ef5256c3c5e31d8f.png)
est l'original de 
On obtient donc :![[f(t).U(t)]^' \,](d/72d453823374266d43538be9addacd24.png)
est l'original de 
Dériver une fonction d'origine revient donc à multiplier son image par p.Formule de la translation à droite
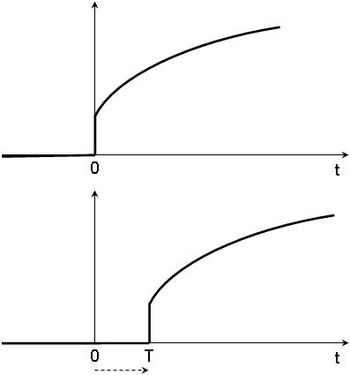
Représentation de la translation d'une fonction d'une valeur « T » à droite.Soit une fonction f(t)U(t) à laquelle on fait subir une translation de la valeur « T » à droite et parallèlement à l'axe des « t » (voir représentations ci-dessus) de telle façon que :
pour 
, et
pour 
.
La forme d'origine est
. Son image est :
.
En posant
on obtient : 
-
.
Conclusion :- avec
: 
est la fonction origine de , avec , et
pour .
Transformation des intégrales
Formule du produit (de Borel)
Fonctions périodiques
Calcul d'intégrales
Extension de la factorielle
Application aux équations différentielles linéaires
Ainsi à l'équation différentielle :
- avec A, B, C, D étant des constantes et les conditions initiales définies en
,
correspond une équation algébrique image de
:
![p\int_0^{+\infty} e^{-pt}. t.dt = -\int_0^{+\infty} t.d(e^{-pt}) = - [t.e^{-pt}]_0^{+\infty} +\int_0^{+\infty} e^{-pt}dt
\,](1/2d11ce63fe8e220e59d7141f90c4bb6a.png)
![p\int_0^{+\infty} e^{-pt}.e^{at}dt = \frac{p}{a-p}.[e^{(a-p)t}]_0^{+\infty}
\,](4/e042a74ea3e544d7074d36ff964fb99f.png)
![\int_0^{+\infty} e^{-pt}.g(t).dt = \int_{0}^{\epsilon} e^{-pt}.\frac{1}{\epsilon}dt = \frac{1}{\epsilon}.[-e^{-pt}]_0^{\epsilon}\,](3/903eab26c745e41427966e0df8901aca.png)
Wikimedia Foundation. 2010.
