Théorème des accroissements finis

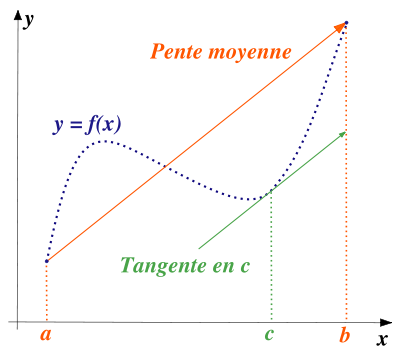
Théorème des accroissements finis
Il existe un point c où la pente de la tangente est la pente moyenne

En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d'une variable réelle, son accroissement entre deux valeurs est réalisable comme pente d'une de ses tangentes.

Sommaire

Énoncé

Pour toute fonction réelle d'une variable réelle ƒ : [a, b] → \R (a et b réels tels que a < b), supposée continue sur l'intervalle fermé [a, b] et dérivable sur l'intervalle ouvert ]a, b[, il existe un réel c strictement compris entre a et b vérifiant :

f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}.

Graphiquement, le théorème des accroissements finis indique que, pour toute sécante d'une courbe différentiable, il existe une tangente parallèle à la sécante. Pour donner une image, on peut illustrer ainsi le théorème : « Si un véhicule parcourt une distance à la vitesse moyenne de 60km/h, alors son compteur a indiqué au moins une fois la vitesse précise de 60 km/h. »

Démonstration

Sous les hypothèses de l'énoncé, la fonction

g:x \mapsto f(x)-f(a) - {f(b)-f(a) \over b-a} \times (x-a)

prend la même valeur en a et en b. En lui appliquant le théorème de Rolle, elle admet un point critique c strictement entre a et b. En ce point c, l'annulation de la dérivée implique l'égalité ci-dessus.

Inégalité des accroissements finis

Soit f : [a, b] → R une fonction à valeurs réelles (a et b réels tels que a < b). Si :

  • f est continue sur l'intervalle fermé [a, b]
  • f est dérivable sur l'intervalle ouvert ]a, b[
  • k est un réel tel que, pour tout élément x de ]a, b[, |f'(x)| ≤ k,

alors \left|{{f(b)-f(a)} \over {b-a}}\right| \le k

Propriété que l'on peut illustrer par: « Si la vitesse instantanée d'un véhicule ne peut pas dépasser 120 km/h, alors sa vitesse moyenne non plus. »

Démonstration 

On applique le théorème des accroissements finis et on majore |f'(c)| par k.

Il existe aussi une inégalité des accroissements finis pour les fonctions à valeurs vectorielles, bien qu'il n'existe pas pour ces fonctions d'analogue du théorème (avec égalité) des accroissements finis.

Théorème des accroissements finis généralisé

Ce théorème s'applique dans le cas de deux fonctions continues sur [a ; b] , dérivables sur ]a ; b[. Il stipule qu'il existe un réel c de l'intervalle ]a ; b[ tel que

(f(b) - f(a))g'(c) - (g(b) - g(a))f'(c) = 0\,

Géométriquement, cette égalité signifie que toute courbe représentative d'une fonction de \R dans \R{}^2 différentiable possède une tangente parallèle à l'une quelconque de ses cordes. Dans le cas où g' ne s'annule pas sur ]a ; b[ , l'égalité peut s'écrire

\frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f'(c)}{g'(c)}

Sous cette forme, le théorème est appelé théorème de la moyenne de Cauchy. Il peut être utilisé pour démontrer la règle de L'Hôpital.

Démonstration 
On applique le théorème de Rolle à la fonction
h(t) = (f(b) - f(a))(g(t) - g(b)) - (g(b) - g(a))(f(t) - f(b))\,
La fonction h est bien continue sur [a ; b], dérivable sur ]a ; b[, et s'annule en a et b par conséquent h(a) = h(b). Donc il existe un réel c de ]a ; b[ tel que h'(c) = 0. Ce qui donne
(f(b) - f(a))g'(c) - (g(b) - g(a))f'(c) = 0\,
Si de plus g’ ne s'annule pas sur ]a ; b[, par contraposée du théorème de Rolle, on peut affirmer que g(b) \ne g(a) et il suffit de diviser par ces deux quantités pour obtenir
\frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f'(c)}{g'(c)}

Théorème des accroissements finis et intégration

Le théorème des accroissements finis se reformule sous forme intégrale. Pour toutes fonctions d'une variable réelle u et v continues sur le segment [a, b], v ne s'annulant pas sur [a, b], il existe un réel c de ]a, b[ tel que

\int_a^b u(t)v(t) \, \mathrm{d}t = u(c) \int_a^b v(t)\, \mathrm{d}t.

L'écriture a un sens car les fonctions continues sont localement intégrables au sens de Riemann.

L'identité ci-dessus se prouve en appliquant le théorème des accroissements finis généralisé à des primitives F et V respectivement de uv et v. Comme la dérivée de V, à savoir v, ne s'annule pas par hypothèses, il existe en effet un réel c dans l'intervalle ]a, b[ vérifiant :

\frac{F(b) - F(a)}{V(b) - V(a)} = \frac{F'(c)}{V'(c)},

Ce qui se réécrit plus simplement :

\frac{\int_a^b u(t)v(t)\, \mathrm{d}t}{\int_a^bv(t)\, \mathrm{d}t}= \frac{u(c)v(c)}{v(c)} = u(c).

Exemple : pour une fonction v constante égale à 1, on retrouve ainsi le théorème de la moyenne : pour toute fonction continue à une variable réelle u sur le segment [a, b], il existe un réel c vérifiant :

u(c)=\frac{1}{b-a}\int_a^b u(t)\, \mathrm{d}t .

Dans Rn

Soient \, f une fonction réelle dérivable sur un ouvert \Omega\in\R^n, \, x un point de \,\Omega et \,h=(h_1, ..., h_n) un point de \R^n tel que

\prod_{i=1}^n [x_i, x_i+h_i]=K\subset\Omega

alors il existe \,\xi^{(1)}, \xi^{(2)}, ...,\xi^{(n)}\in K tels que

f(x+h)-f(x)= \sum_{k=1}^n h_k\frac{\partial f}{\partial x_k}(\xi^{(k)})=\sum_{k=1}^n h_k\frac{\partial f}{\partial x_k}(x+\Delta^{(k)})

avec \,|\Delta^{(k)}|=|x-\xi^{(k)}|<|h| .

En cinématique, pour déterminer l'orientation de la tangente, on utilise la corde
il s'écoule 0,04 s entre le relevé de deux points.

Application en cinématique

En cinématique, le vecteur vitesse d'un point d'un mobile est tangent à la trajectoire de ce point. À partir d'un enregistrement du mouvement (succession de positions relevées à intervalle de temps constant), on peut déterminer la direction du vecteur vitesse au point i en considérant la corde (Mi-1Mi+1).

En effet, sur un petit intervalle, la pente de la tangente varie peu, donc on estime que la valeur en Mi vérifie le théorème des accroissements finis.


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème des accroissements finis de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Theoreme des accroissements finis — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Théorème des accroissements finis généralisé — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Inégalité des accroissements finis — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Égalité des accroissements finis — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Inegalite des accroissements finis pour les fonctions a valeurs vectorielles — Inégalité des accroissements finis pour les fonctions à valeurs vectorielles La majoration des accroissements finis est une adaptation de l inégalité des accroissements finis pour des fonctions à variable réelle et à valeurs vectorielles.… …   Wikipédia en Français

  • Inégalité Des Accroissements Finis Pour Les Fonctions À Valeurs Vectorielles — La majoration des accroissements finis est une adaptation de l inégalité des accroissements finis pour des fonctions à variable réelle et à valeurs vectorielles. Énoncé : Soit E un espace vectoriel normé, et f une fonction définie sur un… …   Wikipédia en Français

  • Inégalité des accroissements finis pour les fonctions à valeurs vectorielles — La majoration des accroissements finis est une adaptation de l’inégalité des accroissements finis pour des fonctions à variable réelle et à valeurs vectorielles. Énoncé : Soient a < b deux réels, E un espace vectoriel normé et deux… …   Wikipédia en Français

  • Theoreme des bornes — Théorème des bornes La fonction atteint ses bornes en c et d En mathématiques, et plus particulièrement en analyse, le théorème des bornes est un théorème qui stipule qu une fonction qui est continue sur un segment de …   Wikipédia en Français

  • Théorème des bornes — Pour les articles homonymes, voir Théorème de Weierstrass. En mathématiques, et plus précisément en analyse réelle, le théorème des bornes ou théorème des bornes atteintes[1] ou théorème de Weierstrass stipule qu une fonction continue sur un… …   Wikipédia en Français

  • Inégalité des accroissement finis — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”