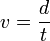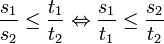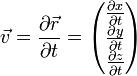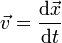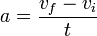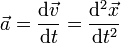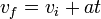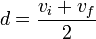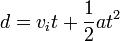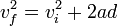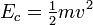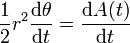Vecteur vitesse

Vecteur vitesse

Vitesse

Page d'aide sur l'homonymie Pour les articles homonymes, voir Vitesse (homonymie).

Sommaire

Définition

  • En physique, la vitesse est une grandeur qui mesure le rapport d'une évolution au temps. Exemple: vitesse de sédimentation, vitesse d'une réaction chimique, etc.
  • En cinématique, la vitesse est une grandeur vectorielle qui mesure pour un mouvement, le rapport de la distance parcourue au temps.

Vitesse en cinématique

On distingue :

  • La vitesse curviligne, qui est la distance d parcourue sur une unité de temps t. C'est une grandeur scalaire.
v = \frac{d}{t}
  • Le vecteur-vitesse ou la vitesse dans l'espace, qui est le vecteur
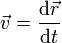
\vec{v} = \frac{\mathrm d\vec{r}}{\mathrm dt}
dont la norme vaut la vitesse et dont le sens et la direction sont ceux du mouvement de l'objet considéré. Formellement, le vecteur-vitesse est la dérivée de la position de l'objet par rapport au temps. Lorsque cela n'entraîne pas de confusions, on appelle le vecteur-vitesse simplement « vitesse ». C'est ici une grandeur vectorielle.

L'unité internationale de la vitesse est le mètre par seconde (m.s-1). Pour les véhicules automobiles, on utilise aussi fréquemment le kilomètre par heure (km/h), le système anglo-saxon utilise le mille par heure (mile per hour, mph). Dans la marine, on utilise le nœud, qui vaut un mille marin par heure, soit 0,514 4 m.s-1. En aviation, on utilise parfois le mach, mach 1 étant la vitesse du son (qui varie en fonction de la température et de la pression).

Histoire du concept de vitesse

Une définition formelle a longtemps manqué à la notion de vitesse, car les mathématiciens s'interdisaient de faire le quotient de deux grandeurs non homogènes. Diviser une distance par un temps leur paraissaient donc aussi faux que pourrait nous sembler aujourd'hui la somme de ces deux valeurs. C'est ainsi que pour savoir si un corps allait plus vite qu'un autre, Galilée (1564-1642) comparait le rapport des distances parcourues par ces corps avec le rapport des temps correspondant. Il appliquait pour cela l'équivalence suivante:

\frac{s_1}{s_2}\le \frac{t_1}{t_2} \Leftrightarrow \frac{s_1}{t_1}\le\frac{s_2}{t_2}

La notion de vitesse instantanée est définie formellement pour la première fois par Pierre Varignon (1654-1722) le 5 juillet 1698, comme le rapport d'une longueur infiniment petite dx sur le temps infiniment petit dt mis pour parcourir cette longueur. Il utilise pour cela le formalisme du calcul différentiel mis au point quatorze ans plus tôt par Leibniz (1646-1716).

Le concept de vitesse

Il faut distinguer deux types de vitesse :

  • la vitesse moyenne, qui répond très précisément à la définition élémentaire. Elle se calcule en divisant la distance parcourue par le temps de parcours ; elle a un sens sur une période donnée ;
  • la vitesse instantanée, qui est obtenue par passage à la limite de la définition de la vitesse. Elle est définie à un instant précis, via la notion de dérivation 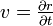v = \tfrac{\partial r}{\partial t}. Par exemple dans les calculs de cinématique, la vitesse est un vecteur obtenu en dérivant les coordonnées cartésiennes de la position par rapport au temps :
\vec{v} = \frac{\partial \vec{r}}{\partial t}=\begin{pmatrix} \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial t} \\ \frac{\partial z}{\partial t} \end{pmatrix}

Vecteur-vitesse

Le vecteur-vitesse instantanée 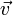\vec v d'un objet dont la position au temps t est donné par 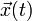\vec x(t) calculé comme la dérivée

\vec v = \frac {\mathrm d\vec x}{\mathrm dt}

L'accélération est la dérivée de la vitesse, et la vitesse est la dérivée de la distance, par rapport au temps.

L'accélération est le taux de changement de la vitesse d'un objet sur la période. L'accélération moyenne a d'un objet dont la vitesse change à partir de vi à vf pendant une période t est donnée par :

a = \frac {v_f - v_i} t

Le vecteur d'accélération instantanée 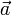\vec a d'un objet dont la position au temps t est donné par 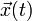\vec x(t) est

\vec a = \frac {\mathrm d\vec v} {\mathrm dt} = \frac {\mathrm d^2\vec x} {\mathrm dt^2}

La vitesse finale vf d'un objet démarrant avec la vitesse vi puis accélérant avec un taux constant a pendant un temps t est:

v_f = v_i + a t \,

La vitesse moyenne d'un objet subissant une accélération constante est 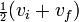{\scriptstyle\frac12}(v_i + v_f). Pour trouver le déplacement d d'un tel objet accélérant pendant la période t, substituer cette expression dans la première formule pour obtenir :

d = \frac {v_i + v_f} 2

Quand seule la vélocité initiale de l'objet est connue, l'expression

d = v_i t + \frac{1}{2}a t^2

peut être utilisée. Ces équations de base pour la vélocité finale et déplacement peuvent être combinées pour former une équation qui est indépendante du temps :

v_f^2 = v_i^2 + 2 a d

Les équations ci-dessus sont valides pour à la fois la mécanique classique mais pas pour la relativité restreinte. En particulier en mécanique classique, tous seront d'accord sur la valeur de t et les règles de transformation pour la position créent une situation dans laquelle tous les observateurs n'accélérant pas décriraient l'accélération d'un objet avec les mêmes valeurs. Ni l'un ni l'autre ne sont vrais pour la relativité restreinte.

L'énergie cinétique d'un objet se déplaçant en translation est linéaire avec sa masse et le carré de sa vitesse :

E_c = \tfrac1 2 mv^2

L'énergie cinétique est une quantité scalaire.

Coordonnées polaires

En coordonnées polaires, la vitesse dans le plan peut être décomposée en vitesse radiale, dr / dt, s'éloignant ou allant vers l'origine et la vitesse orthoradiale, dans la direction perpendiculaire (que l'on ne confondra pas avec la composante tangentielle), égale à 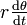r\tfrac{\mathrm d\theta}{\mathrm dt} (voir vitesse angulaire).

Le moment angulaire dans le plan est

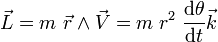\vec L= m\ \vec r \wedge \vec V = m\; r^2\; \frac{\mathrm d \theta}{\mathrm d t} \vec k.

On reconnaît dans

\frac{1}{2}r^2\frac{\mathrm d \theta}{\mathrm d t} = \frac{\mathrm d A(t)}{\mathrm d t}

la vitesse aréolaire.

Si la force est centrale (voir mouvement à force centrale), alors la vitesse aréolaire est constante (deuxième loi de Kepler).

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Vitesse ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Vecteur vitesse de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • vecteur vitesse — greičio vektorius statusas T sritis fizika atitikmenys: angl. velocity vector vok. Geschwindigkeitsvektor, m rus. вектор скорости, m pranc. vecteur de vitesse, m; vecteur vitesse, m …   Fizikos terminų žodynas

  • Vecteur vitesse angulaire — ██████████10  …   Wikipédia en Français

  • Vecteur de Laplace-Runge-Lenz — Vecteur de Runge Lenz Dans cet article les vecteurs et leurs normes sont indiqués respectivement en gras et italique. Par exemple : . En mécanique classique, le vecteur de Runge Lenz ou invariant de Runge Lenz est un vecteur utilisé… …   Wikipédia en Français

  • vitesse — [ vitɛs ] n. f. • 1536; vistece « habileté » 1170; de vite 1 ♦ Le fait ou le pouvoir de parcourir un grand espace en peu de temps. ⇒ célérité, rapidité, vélocité. Se presser « pour gagner les autres de vitesse » (Renan). Lutter de vitesse avec… …   Encyclopédie Universelle

  • Vitesse de rotation — Vitesse angulaire Pour les articles homonymes, voir pulsation (homonymie). En physique, et plus spécifiquement en mécanique, la vitesse angulaire ω, aussi appelée fréquence angulaire ou pulsation, est une mesure de la vitesse de rotation. Elle s… …   Wikipédia en Français

  • Vecteur de killing conforme — En géométrie riemannienne, un vecteur de Killing conforme ou un champ de vecteurs de Killing conforme ou un champ conforme est un champ de vecteurs correspondant à une variation infinitésimale d une isotopie conforme pour une métrique… …   Wikipédia en Français

  • Vecteur Position — Sommaire 1 Définition 2 Écriture d un vecteur 2.1 Coordonnées cartésiennes 2.2 Coordonnées polaires …   Wikipédia en Français

  • Vitesse relative — L expression vitesse relative est communément utilisée, pour exprimer la différence des vitesses de deux mobiles ou la variation dans le temps de la distance entre deux mobiles. Elle est aussi employée pour exprimer des variations comparées par… …   Wikipédia en Français

  • Vecteur de Runge-Lenz — Dans cet article les vecteurs et leurs normes sont indiqués respectivement en gras et italique. Par exemple : . En mécanique classique, le vecteur de Runge Lenz ou invariant de Runge Lenz est un vecteur utilisé principalement pour décrire la …   Wikipédia en Français

  • Vecteur — Pour les articles homonymes, voir Vecteur (homonymie). Deux vecteurs et et le vecteur somme. En …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”