Inegalite des accroissements finis pour les fonctions a valeurs vectorielles

Inegalite des accroissements finis pour les fonctions a valeurs vectorielles

Inégalité des accroissements finis pour les fonctions à valeurs vectorielles

La majoration des accroissements finis est une adaptation de l'inégalité des accroissements finis pour des fonctions à variable réelle et à valeurs vectorielles.

Énoncé : Soit E un espace vectoriel normé, et f une fonction définie sur un segment non vide de \R, [a,b], à valeurs dans E. g est une fonction réelle définie sur [a,b]. On suppose que f et g sont continues sur [a,b], dérivables sur ]a,b[ et que :

\forall t \in ]a,b[, ||f'(t)|| \leq g'(t)

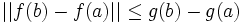On peut alors dire que ||f(b) - f(a)|| \leq g(b) - g(a) .

Ce théorème est d'autant plus surprenant qu'il n'existe pas de théorème de Rolle vectoriel, ou, ce qui revient au même, il n'y a pas d'égalité des accroissements finis, mais seulement une inégalité, comme en témoigne la fonction définie par \forall t \in [0,2\pi], f(t) = e^{it}. On a f(0) = f(2π), mais la dérivée ne s'annule nulle part entre 0 et 2π.

On en déduit par exemple qui si une fonction est dérivable et que sa dérivée est nulle, alors cette fonction est constante.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « In%C3%A9galit%C3%A9 des accroissements finis pour les fonctions %C3%A0 valeurs vectorielles ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Inegalite des accroissements finis pour les fonctions a valeurs vectorielles de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Inégalité Des Accroissements Finis Pour Les Fonctions À Valeurs Vectorielles — La majoration des accroissements finis est une adaptation de l inégalité des accroissements finis pour des fonctions à variable réelle et à valeurs vectorielles. Énoncé : Soit E un espace vectoriel normé, et f une fonction définie sur un… …   Wikipédia en Français

  • Inégalité des accroissements finis pour les fonctions à valeurs vectorielles — La majoration des accroissements finis est une adaptation de l’inégalité des accroissements finis pour des fonctions à variable réelle et à valeurs vectorielles. Énoncé : Soient a < b deux réels, E un espace vectoriel normé et deux… …   Wikipédia en Français

  • Inégalité des accroissements finis — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Inégalité des accroissement finis — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Théorème des accroissements finis — Il existe un point c où la pente de la tangente est la pente moyenne En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre …   Wikipédia en Français

  • Theoreme des accroissements finis — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Théorème des accroissements finis généralisé — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Égalité des accroissements finis — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”