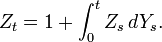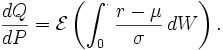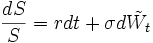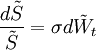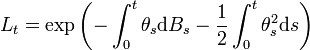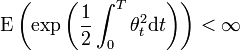- Théorème de girsanov
-
Théorème de Girsanov
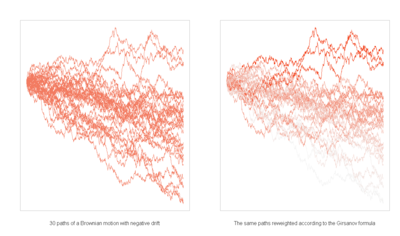 Visualisation du théorème de Girsanov — Le coté gauche montre un processus de Wiener avec une tendance négative sous la mesure canonique P; sur le coté droit, chaque trajectoire du processus est colorée selon sa vraisemblance sous la mesure martingale Q. La densité de Q par rapport à P est donnée par le théorème de Girsanov.
Visualisation du théorème de Girsanov — Le coté gauche montre un processus de Wiener avec une tendance négative sous la mesure canonique P; sur le coté droit, chaque trajectoire du processus est colorée selon sa vraisemblance sous la mesure martingale Q. La densité de Q par rapport à P est donnée par le théorème de Girsanov.
Dans la théorie des probabilités, le théorème de Girsanov indique comment un processus stochastique change si l'on change de mesure. Ce théorème est particulièrement important dans la théorie des mathématiques financières dans le sens où il donne la manière de passer de la probabilité historique qui décrit la probabilité qu'un actif sous-jacent (comme le prix d'une action ou un taux d'intérêt) prenne dans le futur une valeur donnée à la probabilité risque neutre qui est un outil très utile pour évaluer la valeur d'un dérivé du sous-jacent.
Sommaire
Historique
Des résultats de ce type ont été prouvés pour la première fois dans les années 1940 par Cameron-Martin puis en 1960 par Girsanov. Par la suite ils ont été étendus à des classes plus vastes de processus allant en 1977 jusqu'à la forme générale de Lenglart.
Énoncé du théorème
Dans un premier temps, nous énoncerons le théorème dans le cas où le processus sous-jacent est un processus de Wiener. Ce cas particulier est suffisant pour le pricing sous probabilité risque neutre du modèle de Black-Scholes.
Soit {Wt} un processus de Wiener dans l'espace de probabilité
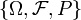 .
.Soit Xt un processus mesurable adapté à la filtration naturelle de {Wt},
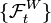 ; nous faisons l'hypothèse que les conditions usuelles sont satisfaites.
; nous faisons l'hypothèse que les conditions usuelles sont satisfaites.Étant donné un processus Xt, on définit
où
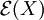 est l'exponentielle stochastique de X par rapport à W, i.e.
est l'exponentielle stochastique de X par rapport à W, i.e.Si Zt est une martingale alors une mesure Q peut être définie sur {σ,F} avec la densité de Radon-Nikodym.
Alors, pour tout t la mesure Q restreinte aux ensembles
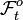 -mesurables est équivalente à P restreinte aux ensembles
-mesurables est équivalente à P restreinte aux ensembles 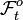 -mesurables.
-mesurables.De plus, si Y est une martingale locale sous P alors le processus
est une Q-martingale locale par rapport à la filtration
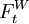 .
.Corollaire
Si X est un processus continu et W est un mouvement brownien sous P alors
![\tilde W_t =W_t - \left [ W, X \right]_t](/pictures/frwiki/52/464776f90a2cc4cb381e27a89f73463c.png) est brownien sous Q.
est brownien sous Q.
La continuité de
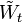 est triviale; selon le théorème de Girsanov, c'est une martingale locale sous Q, or :
est triviale; selon le théorème de Girsanov, c'est une martingale locale sous Q, or :Ce qui correspond à la caractérisation de Lévy du mouvement brownien sous Q.
Commentaires
- Dans de nombreuses applications usuelles, le processus X est défini par
Pour un processus X de cette forme, une condition suffisante pour que X soit une martingale est la condition de Novikov :
- L'exponentiel stochastique
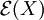 est le processus Z qui satisfait l'équation différentielle stochastique
est le processus Z qui satisfait l'équation différentielle stochastique
Application à la finance
Ce théorème peut être utilisé pour trouver l'unique probabilité risque neutre dans le modèle de Black-Scholes.
Ainsi, si un actif suit le processus de diffusion vérifiant :
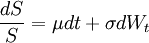 où Wt est un P-mouvement brownien.
où Wt est un P-mouvement brownien.
En effectuant le changement de probabilité suivant :
On obtient une diffusion vérifiant :
Où
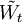 est un Q-mouvement brownien.
est un Q-mouvement brownien.
Si on note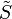 la valeur actualisée de S, on a :
la valeur actualisée de S, on a :Sous la probabilité Q la valeur de notre actif réactualisée est martingale.
Autre énoncé du théorème
Soit
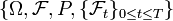 un espace probabilisé, muni de la filtration naturelle par rapport au processus de Wiener standard
un espace probabilisé, muni de la filtration naturelle par rapport au processus de Wiener standard 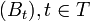 . Soit
. Soit 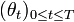 un processus adapté tel que :
un processus adapté tel que :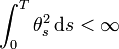 P-f.s. et tel que le processus
P-f.s. et tel que le processus 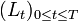 défini par:
défini par:soit une martingale.
Alors sous la probabilité P(L) de densité LT par rapport à P, le processus
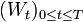 défini par
défini par 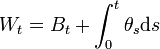 est un Wiener standard.
est un Wiener standard.Condition de Novikov
Der schwierigste Teil in der Anwendung des obigen Satzes ist es wohl zu zeigen, dass Lt Martingal ist. Eine hinreichende Bedingung so dass
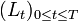 ein Martingal ist, lautet:
ein Martingal ist, lautet:Diese Bedingung nennt man auch die Novikov-Bedingung.
Références
- C. Dellacherie and P.-A. Meyer, "Probabilités et potentiel -- Théorie de Martingales" Chapitre VII, Hermann 1980.
- E. Lenglart "Transformation de martingales locales par changement absolue continu de probabilités", Zeitschrift für Wahrscheinlichkeit 39 (1977) pp 65-70.
Voir aussi
Liens internes
Lien externe
- Notes on Stochastic Calculus qui contient une preuve du théorème de Girsanov.
- Portail des mathématiques
Catégories : Processus stochastique | Théorème de mathématiques
Wikimedia Foundation. 2010.

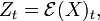
![\mathcal{E}(X)_t=\exp \left ( X_t - \frac{1}{2} [X]_t \right ).](/pictures/frwiki/48/014251f0b804b54012b21b511d43628b.png)
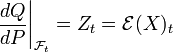
![\tilde Y_t = Y_t - \left[ W,X \right]_s](/pictures/frwiki/55/7fe79e856d763bde56f97b04c4637797.png)
![\left[\tilde W \right]_t= \left [ W \right]_t = t](/pictures/frwiki/102/fafc34d30d91e4faa09e0fcecbc6aaf0.png)
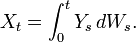
![E_P\left [\exp\left (\int_0^T Y_s^2\, ds\right )\right ] < \infty.](/pictures/frwiki/54/634f07909a856e8c53986bd6307c1513.png)