Somme de minkowski

Somme de Minkowski

En géométrie, la somme de Minkowski est une opération sur les parties d'un espace euclidien. À deux parties A et B elle associe leur ensemble somme, formé des sommes d'éléments de A et de B :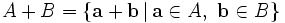

$A + B = \{\mathbf{a}+\mathbf{b}\,|\,\mathbf{a}\in A,\ \mathbf{b}\in B\}$

La somme de deux compacts est compact, il est ainsi possible de restreindre l'opération à cet ensemble, qui peut être munis d'une distance, dite de Hausdorff. La somme de Minkowski est alors une opération continue. De plus elle respecte les convexes, c'est-à-dire que la somme de deux convexes est encore convexe. La mesure de la somme de deux convexes vérifie une majoration, dite inégalité de Brunn-Minkowski.

La somme de Minkwoski intervient dans de nombreux domaines des mathématiques pures ou appliquées. Cet outils est à la base de nombreuses démonstrations de théorèmes isopérimétriques, visant à déterminer la partie de l'espace de plus vaste volume possible, la contrainte étant la donnée de la mesure de sa frontière. En géométrie euclidienne, on trouve les sphères de dimension n. La somme de Minkowski intervient aussi pour le comptage du nombre de face d'un polyèdre, résoudre des questions de pavages ou encore pour étudier la géométrie des convexes. Ils sont appliqués par exemple en cristallographie pour des raisons de pavages d'espace, en économie pour optimiser les productions possibles d'un groupe d'entreprises, ou encore pour étudier les mélanges.

Sommaire

1 Préambule
- 1.1 Exemples
- 1.2 Premières propriétés
2 Formule de Steiner-Minkowski
3 Inégalité de Brunn-Minkowski
4 Notes et références

Préambule

Exemples

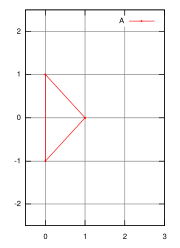
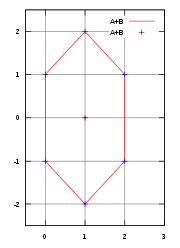
L'ensemble de A à gauche est un triangle dont les coordonnées des sommets sont (0,-1), (0,1) et (1,0). A droite est illustré un triangle semblable B, orienté différemment. Les coordonnées sont (0,0), (1,-1) et (1,1). Si les ensembles A et B sont deux triplets, on trouve :

A + B = {(1, 0), (2, 1), (2, −1), (0, 1), (1, 2), (1, 0), (0, −1), (1, 0), (1, −2)}

Si A et B sont les triangles illustrés en rouge, on trouve un hexagone, illustré par la figure en bas à droite.

De manière générale, la somme de deux polygones est encore un polygone. Cette propriété est vraie pour un polyèdre de dimension quelconque.

On peut remarquer l'analogie entre la somme de Minkowski et le produit de convolution. De manière imagée, on peut obtenir la surface de la somme A + B de deux ensembles en couvrant B de peinture et en faisant parcourir à son centre la surface A. Pour cette raison, cette somme de Minkowski est parfois appelée convolution de A et de B.

De manière évidente, la somme d'un ensemble A et d'un singleton {b} correspond à la translation de A par le vecteur b.

Il n'est guère plus complexe de se rendre compte que la somme de deux carrés est encore un carré. D'une manière plus générale, si C est un convexe, symétrique par rapport à l'origine, la somme C + C est égal au convexe 2C, ici 2C désigne l'homothétie de rapport 2. La démonstration est un peu plus subtile, elle est analogue au lemme préliminaire utilisé dans la démonstration du théorème de Minkowski. Pour s'en rendre compte, on peut remarquer que tout élément de 2C est élément de C + C, réciproquement soit u + v un élément de C + C, il s'écrit aussi comme le double de 1/2(u + v), or cet élément est dans C.

On peut citer un dernier exemple, que l'on trouve dans l'article théorème isopérimétrique. Soient C un compact convexe d'un plan euclidien et P un polygone convexe dont les sommets sont tous sur la frontière de C et dont la plus grande arête est d'une longueur majorée par ε. Alors la somme de P et du disque de centre le vecteur nul et de rayon ε contient le compact convexe C. Cette propriété est une étape pour établir qu'il n'existe aucune surface d'aire plus grande que le disque de même périmètre.

Premières propriétés

Cette opération est commutative, associative, possède pour élément neutre le singleton {0}. Elle est en outre distributive par rapport à la réunion

$A+(B \cup C) = (A +B)\cup (A + C)$ .

D'un point de vue topologique

la somme de deux parties ouvertes est ouverte (comme réunion de translatées de B par exemple)
la somme de deux parties compactes est compacte (par la propriété de Bolzano-Weierstrass)
la somme de deux partie convexe est convexe
la somme, restreinte aux ensembles non vides fermés et bornés est une opération semi-continue supérieurement (cf Distance de Hausdorff).

Remarque : La somme de deux parties fermées n'est pas nécessairement fermée : par exemple en prenant dans le plan la droite des abscisses et l'hyperbole xy=1, leur somme forme le plan privé d'une droite.

Formule de Steiner-Minkowski

Article détaillé : Formule de Steiner-Minkowski.

Dimension 2

Pour un polygone, l'égalité de Steiner Minkowski est presque évidente.

La formule de Steiner a été découverte pour démontrer le théorème isopérimétrique. En dimension 2, il stipule que si C est une surface de périmètre p, alors son aire est plus petite que celle du disque de périmètre p. Si le périmètre p n'est pas fini, comme par exemple pour un compact construit à l'aide d'une courbe de Koch, la formule reste exacte, mais ne possède plus aucun intérêt. Le théorème prend la forme suivante :

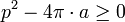
$p^2 - 4\pi\cdot a \ge 0$

L'égalité n'étant obtenue que dans le cas ou le compact C est un disque.

Pour le démontrer, une approche consiste à étudier l'aire de la somme de Minkowski d'un convexe compact C et de t.B, où t désigne un réel positif et B le disque unité, de centre le vecteur nul et de rayon 1. On trouve l'égalité suivante, si μ est la fonction volume qui à C associe son aire, et C est un ensemble convexe :

$\mu(C + t\mathcal B) = a + p\cdot t + \pi \cdot t^2\;$

La fonction volume μ est définie de manière très générale, elle correspond à la mesure de Lebesgue, qui à un carré de coté 1 associe 1. Le périmètre d'une courbe est définie à la manière de Jordan, c'est-à-dire qu'il est égal à la borne supérieure des longueurs de lignes polygonales approximant la frontière. Sous cette forme, démontrer le théorème isopérimétrique revient à montrer que le polynôme du second degré, qui à t associe μ(C + t.B), possède un discriminant positif, ou encore que le polynôme admet une racine réelle.

Cette formule permet aussi d'obtenir une expression du périmètre p, toujours si C est convexe en fonction de la fonction φ:

$\forall t > 0 \quad \varphi(t) = \mu(C + t\mathcal B) \quad\text{alors}\quad p = \frac {d\varphi}{dt}(0)$

Dimension quelconque

Un lampion peut posséder une surface plus grande que celle du cylindre qui le circonscrit.

Il est tentant de généraliser la formule, dans un espace euclidien E de dimension n. On peut considérer la mesure du volume s.C₁ + tC₂, où C₁ et C₂ sont deux compacts convexes et s et t deux réels positifs. On obtient une expression polynomiale du type :

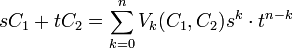
$sC_1 + tC_2 = \sum_{k=0}^n V_k(C_1,C_2) s^k\cdot t^{n-k}\;$

Les coefficients a_k s'appellent volumes mixtes de C₁ et C₂^[1].

On dispose de quelques égalités évidentes :

$V_0(C_1,C_2) = \mu(C_1),\quad V_n(C_1,C_2) = \mu(C_2),\quad V_k(r_1C_1,r_2C_2) = r_1^k\cdot r_2^{n-k} V_k(C_1,C_2)$

Une autre est un peu plus délicate à démontrer dans le cas où C₂ est égal à B :

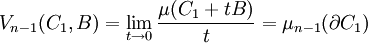
$V_{n-1}(C_1,B) = \lim_{t \to 0} \frac {\mu(C_1 + tB)}t = \mu_{n-1}(\partial C_1)$

Ici, $μ$ _n-1 désigne le volume n - 1 dimensionnel. Définir une mesure n - 1 dimensionnelle devient subtil. Une première méthode consiste à généraliser la technique utilisée en dimension 1, pour un arc rectifiable. Elle demande d'être adaptée et est spécifique aux convexes. La mesure de la surface est alors la borne supérieure des convexes polyédriques inclus dans C₁. La convexité est indispensable, sinon le contre exemple de droite montre que la définition ne fait pas sens. La surface que l'on souhaite mesurer est un cylindre, le polyèdre utilisé est un lampion dont les sommets sont situés sur des hexagones chaque fois décalés d'un douzième de tour. Si les plans des hexagones se rapprochent de plus en plus, la surface du polyèdre augmente jusqu'à l'infini^[2]. Une autre technique consiste à utiliser une forme différentielle et plus précisément une forme volume. La difficulté réside alors dans le fait que la surface d'un convexe n'a pas de raison d'être une variété de classe C¹. Il devient nécessaire d'utiliser des espaces comparables à ceux de Sobolev pour définir la surface.^[3]

Les volumes mixtes vérifient une majoration utilisée pour démontrer le théorème isopérimétrique pour les dimensions supérieures à 2. Elle porte le nom d'inégalité de Alexandrov-Fenchel :^[4]

$\forall i \in [1, n-1]\quad V_k(C_1,C_2)^2 \le V_{k-1}(C_1,C_2)\cdot V_{k+1}(C_1,C_2)$

Démonstrations

Ici, E désigne un espace euclidien de dimension n.

Si P est un polyèdre compact et convexe de E, la fonction qui à (s, t) associe la mesure μ(s.P + t.B) est un polynôme homogène de degré n :

Notons M cette mesure. M est la somme de la mesure μ(s.P) et de la croute ajoutée par la somme de t.B. Le terme associé à la mesure de μ(s.P) est une constante que multiplie sⁿ.

Sur chaque face, on trouve un hypercube H_i¹ de dimension n, de base la face en question et de hauteur t de dimension n - 1 et de mesure le produit d'une constante et de s^n-1. Chacune de ces faces contribue au volume μ(P + t.B) sous la forme d'une expression linéaire en s^n-1.t.

Entre ces hypercubes, on trouve des interstices H_j², ayant la forme d'un prisme, d'arête l'intersection de deux faces, et de dimension n - 2, dont la mesure est le produit d'une constante avec s^n-2 et de cotés deux faces d'hypercubes H_i¹ ayant une arête de longueur t, le sommet un composé du produit d'un disque de rayon t et d'un hypercube isomorphe à l'arête. Ces prismes sont donc des portions de cylindre d'axe un hypercube de dimension n - 2 et de rayon r. Chacune de ces portions de cylindre contribue au volume μ(P + t.B) sous la forme d'une expression en s^n-2.t².

Les arêtes de dimension n - 2 ont comme extrémités des hypercubes de dimension n - 3 qui laissent place à des interstices, laissée vacant par les solides H_i¹ et H_j². Ces interstices H_k<sup3, sont remplis par des primes, d'arêtes les intersections des arêtes précédentes, sont de dimension n - 3 et de mesure le produit d'une constante et de s^n-3. Ces primes correspondent à des portions de produit de boule de dimension 3 et d'hypercubes arêtes de dimension n - 3. Leur somme correspond à une expression en s^n-3.t³.

On continue ainsi jusqu'à la dimension 1, l'intersection des arêtes est alors de dimension 0 et correspond à un point. L'interstice correspond à une portion de boule, dont l'expression est le produit d'une constante par tⁿ.

Le terme en sⁿ correspond à la mesure de P, celui en s^n-1.t à la mesure de la surface de P. Si s est égal à 0, on remarque que le volume est celui d'une boule de rayon t, la constante est celle associée au volume n dimensionnel d'une sphère.

Si C est un compact, convexe non vide de E, la fonction qui à (s, t) associe la mesure μ(s.C + t.B) est un polynôme homogène de degré n :

Soit (C_p) une suite décroissante de polyèdres convexes dont la limite, au sens de Hausdorff, est égale à C. Le paragraphe ensemble dense de l'article Distance de Hausdorff montre qu'une telle suite existe. Soit P_p(s, t) le polynôme homogène de degré n qui à (s, t) associe μ(s.C_p + t.B), l'objectif est de montrer que la suite (P_p) converge simplement.

La suite (s.C_p + t.B) est une suite de compacts, décroissante pour l'inclusion, elle est nécessairement convergente au sens de Hausdorff, montrons que la limite est égale à s.C + t.B. Tout ensemble de la suite contient s.C + t.B, la limite contient donc cet ensemble. Réciproquement si y n'est pas élément de s.C + t.B, il existe un nombre réel strictement positif ε tel que la boule de centre y et de rayon ε ait une intersection nulle avec s.C + t.B car cet ensemble est fermé. On en déduit que tout élément de s.C_n est à une distance supérieure à t + ε de y. Si s n'est pas nul, cela signifie aussi que y est à une distance supérieure à (t + ε)/s de C. A partir d'un certain N, pour toute valeur de p plus grande que N, C_p est à une distance de y strictement supérieure à t/s, et s.C_p + t.B ne peut contenir y. Si s est nul, la suite s.C_p + t.B est constante égale à t.B et est trivialement convergente.

Comme la suite (s.C_p + t.B) est une suite de compacts strictement décroissante, de limite s.C + t.B, et que la fonction μ est semi-continue supérieurement, la suite μ(s.C_p + t.B) est convergente (cf le paragraphe Fonctions continues de l'article Distance de Hausdorff). Ce qui signifie exactement que la suite (P_p) converge simplement.

Chaque polynôme de la suite (P_p) est un polynôme homogène de degré n, cette suite fait partie de l' espace vectoriel des polynômes à deux variables de degré inférieur à n et est de dimension finie. Sur cet espace, la topologie de la convergence simple est compatible avec l'addition et la multiplication externe, ce qui signifie que ces deux opérations sont continues. Or, sur un espace vectoriel réel de dimension finie, il n'existe qu'une topologie compatible avec ses deux opérations, (cf topologie d'un espace vectoriel de dimension finie). Cette topologie est induite par n'importe quelle norme, par exemple celle de la convergence uniforme sur le disque de rayon r, où r désigne un nombre réel strictement positif. L'espace vectoriel des polynômes à deux variables homogènes et de degré n est complet pour cette norme, ce qui montre que la suite (P_p) converge vers un polynôme P homogène de degré n.

Cette limite P est, par construction, la fonction qui à (s, t) associe μ(s.C + t.B), ce qui démontre la proposition.

Inégalité

Inégalité de Brunn-Minkowski

L'égalité de Brunn-Minkowski est une majoration du volume de la somme de deux parties mesurables d'un espace euclidien :

Soient E un espace euclidien de dimension n, μ une mesure de Lebesgue sur E et A et B deux compacts non vides de E. La majoration suivante, appelée inégalité de Brunn-Minkowski est vérifiée^[5] :

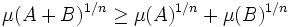
$\mu (A+B)^{1/n}\geq \mu(A)^{1/n}+\mu (B)^{1/n}$

La majoration est illustrée sur la figure de droite. Elle représente la somme d'un hexagone jaune et d'un disque vert. La mesure de la somme est toujours supérieure à la somme des mesures. Sur la figure, l'excédent C est représenté en bleu, la mesure de cet excédent vérifie la majoration suivante :

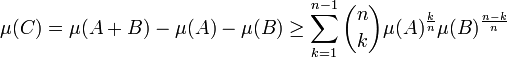
$\mu(C) = \mu(A + B) - \mu(A) - \mu(B) \ge \sum_{k=1}^{n-1} \binom{n}{k} \mu(A)^{\frac kn}\mu(B)^{\frac {n-k}n}$

La majoration est une égalité si, et seulement si, A et B sont deux figures homothétiques.

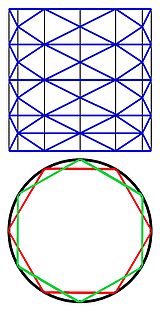
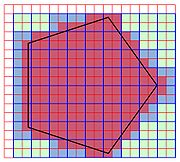
Démonstration

L'espace E est équipé d'une base orthonormale, puis il est quadrillé par une grille composée d'hyperplans dont les directions sont orthogonales à un des vecteurs de la base. Ces hyperplans sont régulièrement espacés, avec un pas de 1/2^p, ou p est un entier strictement positif. Cette grille pave l'espace à l'aide de petits hypercubes d'arêtes de longueur 1/2^p. La mesure de Lebesgue choisie est celle qui associe à un hypercube de coté de longueur 1 la valeur 1.

Ces hypercubes permettent d'approximer un compact. Par exemple, sur la figure de droite un pentagone régulier est approximé par des carrés bleus. Affiner la grille revient à choisir une valeur plus élevée pour p. La figure de droite illustre aussi une deuxième approximation par des petits carrés rouges obtenu pour un incrément de 1 de la valeur p. L'article Distance de Hausdorff montre que cette technique permet de construire une suite (A_n) de compacts contenant A et approximant de plus en plus précisément A, au sens de la distance de Hausdorff.

La démonstration proposée ici^[6] se déroule en trois temps. Dans un premier temps, on la démontre dans le cas où A est un hypercube de la grille et B un hypercube inclus dans un de ceux de la grille et dont les arêtes sont toutes de longueur a = 1/2^p sauf celles parallèles au premier vecteur de la base qui sont de longueur λ.a. Ici, λ désigne un nombre réel strictement positif et plus petit que 1.

Dans le cas où A et B sont deux hypercubes décrits ci-dessus, la majoration de Brunn-Minkowski est vérifiée :

Le cas est suffisamment simple pour permettre un calcul effectif des trois mesures.

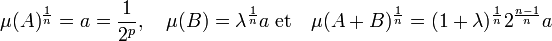
$\mu(A)^{\frac 1n} = a = \frac 1{2^p},\quad \mu(B) = \lambda^{\frac 1n}a\;\text{et}\quad \mu(A+B)^{\frac 1n} = (1+ \lambda)^{\frac 1n}2^{\frac {n-1}n}a\;$

Démontrer la majoration dans le cas présent revient à montrer que la fonction f de ]0,1] dans R, où R désigne l'ensemble des nombres réels, est strictement positif, sur ]0,1[ et nulle en 1.

$\forall t \in ]0,1]\quad f(t) = (1+ \lambda)^{\frac 1n}2^{\frac {n-1}n} - \lambda^{\frac 1n} - 1\;$

Il est clair que la fonction f est nulle au point 1, il suffit de montrer qu'elle est strictement décroissante pour conclure. La fonction f est dérivable sur ]0,1[, il suffit de montrer que sa dérivée est strictement négative, ce qui se vérifie aisément.

$\forall t \in ]0,1[ \quad f'(t) = \frac 1n \left(\left(\frac 2{1 + \lambda}\right)^{\frac {n-1}n} - \left(\frac 1{\lambda}\right)^{\frac {n-1}n}\right) = \frac 1{n\lambda^{\frac {n-1}n}} \left(\left(\frac {2\lambda}{1 + \lambda}\right)^{\frac {n-1}n} - 1\right)<0$

On suppose maintenant que A et B sont deux unions finies d'intérieurs d'hypercubes de la grille ou de partie d'hypercubes ouverts dont une des coordonnées est comprise entre 1/2^p.(δ + λ) et 1/2^p.(δ + 1). C'est-à-dire que les hypercubes sont du type de la proposition précédente. Les valeurs q et r désignent le nombre d'hypercubes composant respectivement A et B.

Dans le cas où A et B sont deux compacts de la forme décrite ci-dessus, la majoration de Brunn-Minkowski est vérifiée :

On raisonne par récurrence sur l'entier s égal à la somme de q et de r. Si s est égal à 2, le résultat est une conséquence directe de la proposition précédente.

On suppose le résultat établi jusqu'à une valeur s₀ et on suppose que la somme de q et de r est égale à s₀ + 1. On sépare l'espace euclidien E en deux connexes par un des hyperplans H_A orthogonal à l'un des vecteurs de la base orthonormale qui définit la grille. Il existe un hyperplan de cette nature qui décompose A en deux ouverts disjoints A₁ et A₂ tel que A₂ comporte au moins un hypercube et tel que A₁ ne soit pas l'ensemble vide. A₁ et A₂ sont alors composés d'au plus de q - 1 hypercubes. On note θ le nombre réel strictement positif suivant :

$\theta = \frac {\mu(A_1)}{\mu (A)} = \frac {\mu(A_1)}{\mu (A_1) + \mu(A_2)}$

On sépare B en deux ensembles B₁ et B₂ par un hyperplan H_B parallèle au précédent, de telle manière à ce que :

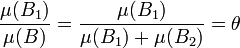
$\frac {\mu(B_1)}{\mu (B)} = \frac {\mu(B_1)}{\mu (B_1) + \mu(B_2)} = \theta$

Ni B₁ et B₂ ne contiennent de vecteurs de l'hyperplan H_B, en conséquence, B contient mais n'est pas nécessairement égal à l'union de B₁ et B₂, mais comme un sous ensemble inclus dans un hyperplan est de mesure nulle, l'égalité précédente est vérifiée. Cette fois ci, rien ne prouve que B₁ et B₂ contiennent moins d'hypercubes que B, mais il est certain qu'ils n'en contiennent pas plus. Les propriétés de la somme de Minkowski montrent que :

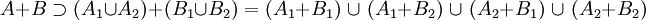
$A + B \supset (A_1\cup A_2) + (B_1 \cup B_2) = (A_1 + B_1) \;\cup\; (A_1 + B_2) \;\cup\; (A_2 + B_1) \;\cup\; (A_2 + B_2)$

Considérons le vecteur de la base orthonormale orthogonale aux deux hyperplans H_A et H_B, les coordonnées sur ce vecteur de tout élément de A₁ + B₁ sont strictement plus petites que celles des vecteurs de A₂ + B₂, ce qui montre que les deux ensembles sont disjoints et :

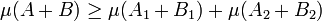
$\mu(A + B) \ge \mu(A_1 + B_1) + \mu (A_2 + B_2)\;$

Comme A₁ et A₂ contiennent strictement moins que q petits hypercubes et que B₁ et B₂ n'en contiennent pas plus que r, il est possible d'appliquer l'hypothèse de récurrence :

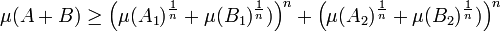
$\mu(A + B) \ge \left(\mu(A_1)^{\frac 1n} + \mu(B_1)^{\frac 1n})\right)^n + \left(\mu(A_2)^{\frac 1n} + \mu(B_2)^{\frac 1n})\right)^n$

Ce que l'on peut encore écrire :

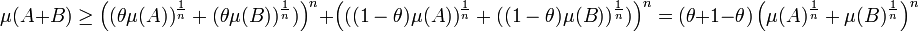
$\mu(A + B) \ge \left((\theta \mu(A))^{\frac 1n} + (\theta \mu(B))^{\frac 1n})\right)^n + \left(((1-\theta) \mu(A))^{\frac 1n} + ((1-\theta) \mu(B))^{\frac 1n})\right)^n = (\theta + 1 - \theta)\left(\mu(A)^{\frac 1n} + \mu(B)^{\frac 1n}\right)^n$

Ce qui montre la majoration qui termine la démonstration :

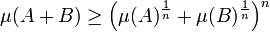
$\mu(A + B) \ge \left(\mu(A)^{\frac 1n} + \mu(B)^{\frac 1n}\right)^n$

Il est maintenant possible de prouver la majoration de Brunn-Minkowski dans le cas général. On utilise pour cela un passage à la limite utilisant la distance de Hausdorff. Soit ε un réel strictement positif et A et B deux compacts de E. L'objectif de la démonstration est de montrer que la somme de la mesure de A + B et de ε majore bien le deuxième membre de l'inégalité. On utilise trois propriétés démontrées dans l'article Distance de Hausdorff.

Si A et B sont deux compacts non vides, l'inégalité de Brunn-Minkowski est vérifiée :

Dans un premier temps, on utilise la semi-continuité supérieure de la fonction mesure pour la distance de Hausdorff. Si E_H désigne l'ensemble des compacts non vides de E et d la distance de Hausdorff :

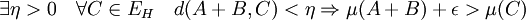
$\exists \eta > 0 \quad \forall C \in E_H \quad d(A + B , C)< \eta \Rightarrow \mu(A + B) + \epsilon > \mu (C)$

Il s'agit maintenant de construire le bon ensemble C. On utilise l'existence de deux ensembles A_ε et B_ε compacts contenant strictement A et B et tel que :

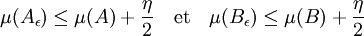
$\mu(A_{\epsilon}) \le \mu(A) + \frac {\eta}2 \quad\text{et}\quad \mu(B_{\epsilon}) \le \mu(B) + \frac {\eta}2$

Les deux ensembles A_ε et B_ε sont des unions finies d'hypercubes fermés de la grille, pour une valeur de p suffisamment élevée. L'existence de tels ensembles provient du fait que les unions finies d'hypercubes fermés pris dans la grille forment un ensemble dense si p décrit les entiers positifs. La démonstration de la continuité de la somme de Minkowski pour la distance de Hausdorff (cf l'article Distance de Hausdorff) montre que :

$d\left(A + B ,A_{\epsilon} + B_{\epsilon}\right) \le \eta \;$

On choisit C égal à la somme de A_ε et B_ε, ce qui montre que :

$\mu(A + B) + \epsilon > \mu\left( A_{\epsilon} + B_{\epsilon}\right)\;$

On retire à l'ensemble A_ε + B_ε son intersection avec les hyperplans de la grille, ce qui ne modifie pas sa mesure. On se trouve alors dans les hypothèses de la proposition précédente et :

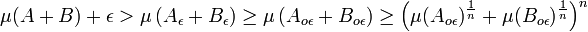
$\mu(A + B) + \epsilon > \mu\left( A_{\epsilon} + B_{\epsilon}\right) \ge \mu\left( A_{o\epsilon} + B_{o\epsilon}\right) \ge \left(\mu(A_{o\epsilon})^{\frac 1n} + \mu(B_{o\epsilon})^{\frac 1n}\right)^n$

Ici, A_oε et B_oε désignent les ensembles A_ε et B_ε otés de leurs intersections avec les hyperplans de la grille. Rajouter cette intersection ne modifie en rien les mesures, ce qui montre que :

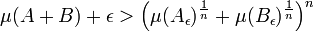
$\mu(A + B) + \epsilon > \left(\mu(A_{\epsilon})^{\frac 1n} + \mu(B_{\epsilon})^{\frac 1n}\right)^n$

Par hypothèse, les ensembles A_ε et B_ε contiennent A et B. Leur mesure est plus grande, et :

$\mu(A + B) + \epsilon > \left(\mu(A)^{\frac 1n} + \mu(B)^{\frac 1n}\right)^n$

Cette majoration est vraie pour toute valeur de ε strictement positive, ce qui montre le résultat cherché.^[7]

Notes et références

Notes

↑ B. Teissier Volumes des corps convexes, géométrie et algèbre Institut de Mathématiques de Jussieu. Leçon donnée le jeudi 7 octobre 1999 Rédigée par C. Reydy, p 8
↑ Cet exemple est tiré de Marcel Berger, Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions] p 226.
↑ Pour plus de détails, voir : H. Federer Geometric Measure Theory Springer-Verlag (1969) (ISBN 3540606564) 3.2.37, 3.2.39, 3.2.26
↑ A.D. Alexandrov Selected Works CRC (2002) (ISBN 2881249841)
↑ Jiri Matousek, Lectures on Discrete Geometry [détail des éditions], p. 297
↑ Elle s'inspire directement d'une généralisation en dimension n de celle-ci, en dimension 2 : A. Treibergs Inequalities that Imply the Isoperimetric Inequality University of Utah p 16
↑ Une démonstration en dimension n est proposée à : R. J. Garnder The Brunn-Minkowski inequality Bulletin (New Series) of the A. M. S. Vol. 39 n° 3 p 363

Liens externes

M. Rousset Sommes de Minkowski de triangles Thèse de troisième cycle, Université Joseph Fourier 1996

Références

(en) H. Federer Geometric Measure Theory Springer-Verlag (1969) (ISBN 3540606564)
(en) B. Dacorogna Introduction to the Calculus of Variations Imperial College Press (2004) (ISBN 1860945082)

Portail des mathématiques

Ce document provient de « Somme de Minkowski ».

Catégorie : Géométrie affine

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Somme de minkowski de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Somme de Minkowski — Pour les articles homonymes, voir Somme. En géométrie, la somme de Minkowski est une opération sur les parties d un espace vectoriel. À deux parties A et B elle associe leur ensemble somme, formé des sommes d éléments de A et de B. On note l… … Wikipédia en Français
Minkowski — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Personnes Hermann Minkowski (1864 1909), mathématicien et physicien théoricien allemand ; Oskar Minkowski (1858 1931), médecin allemand, frère du… … Wikipédia en Français
MINKOWSKI (H.) — MINKOWSKI HERMANN (1864 1909) Mathématicien allemand né en Russie, à Alexoten, et mort à Göttingen. Hermann Minkowski habita Königsberg dès sa plus tendre enfance, et il fit ses études universitaires à Königsberg et à Berlin. De 1887 à 1902, il… … Encyclopédie Universelle
Minkowski, Eugene — (1885–1972) One of the cofounders of the movement Évolution psychiatrique in France, Minkowski was born in St. Petersburg, Russia, of Jewish Lithuanian parents. The family moved to Warsaw when he was 7, and he began medical school there,… … Historical dictionary of Psychiatry
Formule De Steiner-Minkowski — Pour les articles homonymes, voir Steiner et Minkowski. En géométrie, les formules de Steiner Minkowski sont des relations traitant d un compact C d un espace euclidien E. On ajoute en général une condition supplémentaire sur le compact,… … Wikipédia en Français
Formule de Steiner-Minkowski — Pour les articles homonymes, voir Steiner et Minkowski. En géométrie, les formules de Steiner Minkowski sont des relations traitant d un compact C d un espace euclidien E. On ajoute en général une condition supplémentaire sur le compact,… … Wikipédia en Français
Formule de steiner-minkowski — Pour les articles homonymes, voir Steiner et Minkowski. En géométrie, les formules de Steiner Minkowski sont des relations traitant d un compact C d un espace euclidien E. On ajoute en général une condition supplémentaire sur le compact,… … Wikipédia en Français
Hermann Minkowski — Pour les articles homonymes, voir Minkowski. Hermann Minkowski Hermann Minkowski Naissance … Wikipédia en Français
Eugène Minkowski — (* 17. April 1885 in Sankt Petersburg; † 17. November 1972 in Paris) war ein russisch französischer Psychiater und Philosoph. Minkowski wurde als Sohn jüdischer Eltern in Sankt Petersburg geboren. Er ging in Warschau zur Schule und studierte… … Deutsch Wikipedia
Theoreme isoperimetrique — Théorème isopérimétrique En géométrie, un théorème isopérimétrique traite d une question concernant les compacts d un espace métrique muni d une mesure. Un exemple simple est donné par les compacts d un plan euclidien. Les compacts concernés sont … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Somme de minkowski

Somme de Minkowski

Sommaire