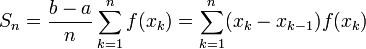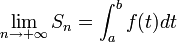Somme de riemann
- Somme de riemann
-
Somme de Riemann
Les sommes de Riemann sont une méthode d'approximation des intégrales. Elles peuvent être utilisées pour définir la notion d'intégrale. Leur nom vient du mathématicien allemand Bernhard Riemann.
Définition
Soit ![f:[a,b]\rightarrow\mathbb{R}](/pictures/frwiki/48/04b1d979a595c58bb6355218396fb44e.png) une fonction continue sur le segment [a,b]. On considère
une fonction continue sur le segment [a,b]. On considère 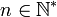 et une subdivision régulière
et une subdivision régulière 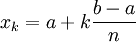 , avec
, avec 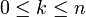 .
.
La somme de Riemann associée à f est alors :
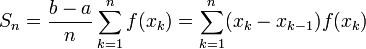
Application
Les sommes de Riemann sont utilisées pour le calcul des intégrales par la méthode des rectangles. En effet :
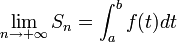
Extensions
- On peut considérer
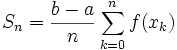 car
car 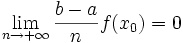 (une seule valeur ne change pas le résultat).
(une seule valeur ne change pas le résultat).
- On peut aussi étendre la propriété précédente aux cas de subdivisions
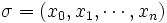 quelconques. Dans ce cas, on note
quelconques. Dans ce cas, on note 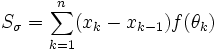 où
où ![\theta_k\in[x_{k-1},x_k]](/pictures/frwiki/50/248d7ba8f52313eb91172c3b2b7c341e.png) . On note
. On note 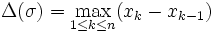 le pas de la subdivision. Donc, avec les notations précédentes, si
le pas de la subdivision. Donc, avec les notations précédentes, si 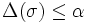 , alors :
, alors : 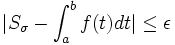 , relation à la source de la définition de l'intégrale de Riemann.
, relation à la source de la définition de l'intégrale de Riemann.
- Si, au lieu de majorer le pas xk − xk − 1 par une constante Δ, on le majore par une quantité δ(tk) où tk est un point de xk − xk − 1 et δ une fonction strictement positive, on remplace l'intégrale de Riemann par l'intégrale de Kurzweil-Henstock.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorie de l'intégration | Bernhard Riemann
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Somme de riemann de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Somme de Riemann — Pour les articles homonymes, voir Somme. En mathématiques, et plus précisément en analyse, les sommes de Riemann sont des sommes approximant des intégrales. Elles peuvent également être utilisées pour définir la notion d intégration. Leur nom… … Wikipédia en Français
Somme (arithmetique) — Somme (arithmétique) Pour les articles homonymes, voir Somme. En mathématiques, la somme de deux nombres est le résultat de leur addition. Elle se calcule de différentes manières selon le système de numération employé. Du fait de la commutativité … Wikipédia en Français
Somme totale — Somme (arithmétique) Pour les articles homonymes, voir Somme. En mathématiques, la somme de deux nombres est le résultat de leur addition. Elle se calcule de différentes manières selon le système de numération employé. Du fait de la commutativité … Wikipédia en Français
Somme (arithmétique) — Pour les articles homonymes, voir Somme. En mathématiques, la somme de deux nombres est le résultat de leur addition. Elle se calcule de différentes manières selon le système de numération employé. Du fait de la commutativité et de l… … Wikipédia en Français
RIEMANN (B.) — Après la mort de Georg Friedrich Bernhard Riemann, son œuvre fut publiée en un seul volume, y compris les fragments posthumes, et cette brièveté ne tient pas seulement à la fin précoce du mathématicien: d’une part, ses démonstrations sont très… … Encyclopédie Universelle
Somme des diviseurs — En arithmétique, la somme des diviseurs d un nombre entier strictement positif est l entier obtenu en effectuant la somme de tous les diviseurs positifs de cet entier. La fonction qui, à l entier n, associe la somme de ses diviseurs est souvent… … Wikipédia en Français
Somme infinie — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini … Wikipédia en Français
Somme partielle — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini … Wikipédia en Français
Riemann hypothesis — The real part (red) and imaginary part (blue) of the Riemann zeta function along the critical line Re(s) = 1/2. The first non trivial zeros can be seen at Im(s) = ±14.135, ±21.022 and ±25.011 … Wikipedia
Integrale de Riemann — Intégrale de Riemann Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann est une façon simple de définir l intégrale d une fonction sur un intervalle. En termes géométriques, cette intégrale s… … Wikipédia en Français
![f:[a,b]\rightarrow\mathbb{R}](/pictures/frwiki/48/04b1d979a595c58bb6355218396fb44e.png) une fonction continue sur le segment [a,b]. On considère
une fonction continue sur le segment [a,b]. On considère 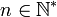 et une subdivision régulière
et une subdivision régulière 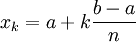 , avec
, avec 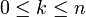 .
.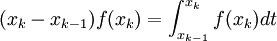 d'où
d'où 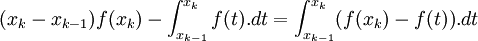
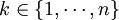 , on obtient :
, on obtient : 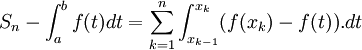 d'où
d'où 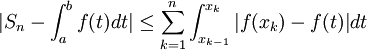
![\forall(x,t)\in[a,b]^2|x-t|\leq\alpha\Rightarrow |f(x)-f(t)|\leq\frac{\epsilon}{b-a}](/pictures/frwiki/97/aa88156afee6abab8094a233c83dad59.png) .
.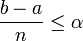 . Ainsi
. Ainsi ![\forall t \in[x_{k-1};x_k] |x_k-t|\leq \frac{b-a}{n}\leq \alpha](/pictures/frwiki/49/1bbe45ffde6851f228ffc6fa52d3351e.png) , d'où
, d'où 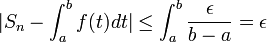 .
.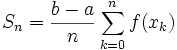 car
car 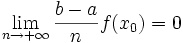 (une seule valeur ne change pas le résultat).
(une seule valeur ne change pas le résultat).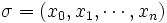 quelconques. Dans ce cas, on note
quelconques. Dans ce cas, on note 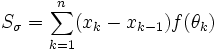 où
où ![\theta_k\in[x_{k-1},x_k]](/pictures/frwiki/50/248d7ba8f52313eb91172c3b2b7c341e.png) . On note
. On note 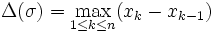 le pas de la subdivision. Donc, avec les notations précédentes, si
le pas de la subdivision. Donc, avec les notations précédentes, si 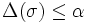 , alors :
, alors : 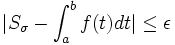 , relation à la source de la définition de l'intégrale de Riemann.
, relation à la source de la définition de l'intégrale de Riemann.