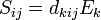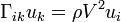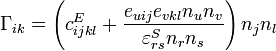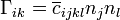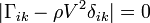- Piézoélectrique
-
Piézoélectricité
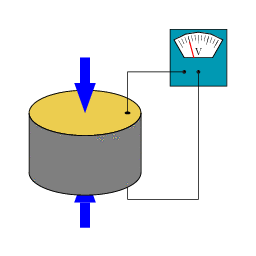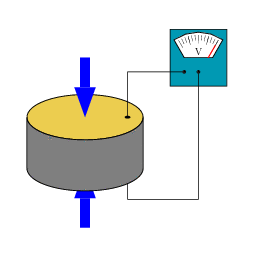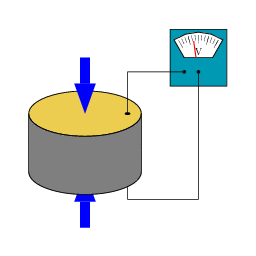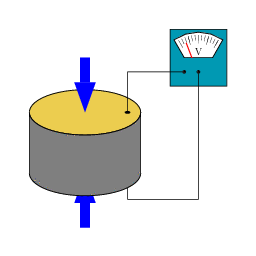 Illustration du comportement d’une pastille piézoélectrique : la contrainte appliquée crée un signal électrique.
Illustration du comportement d’une pastille piézoélectrique : la contrainte appliquée crée un signal électrique.
La piézoélectricité (du grec piézein presser, appuyer) est la propriété que possèdent certains corps de se polariser électriquement sous l’action d’une contrainte mécanique et réciproquement de se déformer lorsqu’on leur applique un champ électrique. Les deux effets sont indissociables. Le premier est appelé effet piézoélectrique direct ; le second effet piézoélectrique inverse.
Cette propriété trouve un très grand nombre d’applications dans l’industrie et la vie quotidienne. Une application parmi les plus familières est l’allume-gaz. Dans un allume-gaz, la pression exercée produit une tension électrique qui se décharge brutalement sous forme d’étincelles : c'est une application de l’effet direct. De manière plus générale, l’effet direct peut être mis à profit dans la réalisation de capteurs (capteur de pression, microbalance…) tandis que l’effet inverse permet de réaliser des actionneurs (injecteurs à commande piézoélectrique en automobile, nanomanipulateur…).
Les matériaux piézoélectriques sont très nombreux. Le plus connu est sans doute le quartz, toujours utilisé aujourd’hui dans les montres pour générer des impulsions d’horloge. Mais ce sont des céramiques synthétiques, les PZT qui sont le plus largement utilisées aujourd’hui dans l'industrie.
Soulignons enfin que l’effet piézoélectrique inverse ne doit pas être confondu avec l’électrostriction qui est un effet du second ordre et existe dans tous les matériaux.
Aspects historiques
Travaux précurseurs
Au milieu du XVIIIe siècle, Carl von Linné et Franz Aepinus avaient étudié l'effet pyroélectrique, par lequel un changement de température entraîne une variation de la polarisation électrique d'un cristal. Le cristal type présentant cet effet est alors la tourmaline : en chauffant un cristal de tourmaline, on fait apparaître sur ses deux faces de l'électricité. La nature de l'électricité est différente sur une face et sur l'autre, vitreuse et résineuse selon les termes de l'époque (on parlerait aujourd'hui de charges positives et négatives).
En 1817, l'abbé René-Just Haüy, qui a étudié en détail la pyroélectricité dans différents minéraux, décrit la découverte de ce qu'il appelle alors « l'électricité de pression » sur le spath d’Islande : en comprimant un cristal entre les doigts, il est possible de faire apparaître de l'électricité sur les faces du cristal. Antoine Becquerel poursuit l'étude du phénomène, il identifie plusieurs autres minéraux présentant cette propriété et montrera à l'aide d'une balance de Coulomb que l'électricité ainsi produite est dans une certaine gamme environ proportionnelle à la pression exercée[1],[2].
Contrairement à la pyroélectricité, Haüy observe que c'est le même type d'électricité qui est produite sur les deux faces du cristal. Cela suffit à dire que le phénomène découvert par Haüy n'est pas de la piézoélectricité. Le spath d’Islande n'est d'ailleurs pas piézoélectrique[3]. Quand ils publieront leurs travaux sur le quartz, les Curie se démarqueront des travaux de Haüy, attribuant l'électricité de pression à un effet de surface.
L'électricité de pression de Haüy aura été pendant une cinquantaine d'années une propriété parmi d'autres permettant de classer les minéraux[4]. Mais le caractère incertain et difficilement reproductible de cet effet le fera tomber dans l'oubli avec la découverte de la piézoélectricité. Au début du XXe siècle, les manuels de minéralogie ne feront plus mention de l'électricité de pression de Haüy.
Découverte de l'effet piézoélectrique
 Pierre Curie (photo) et son frère Jacques firent la première démonstration expérimentale de l'effet piézoélectrique.
Pierre Curie (photo) et son frère Jacques firent la première démonstration expérimentale de l'effet piézoélectrique.
La première démonstration de l'effet piézoélectrique direct est due à Pierre et Jacques Curie en 1880. À cette époque, les deux frères, âgés respectivement de 21 et 25 ans, sont tous deux préparateurs à la faculté des sciences de Paris. Combinant leurs connaissances de la pyroélectricité et de la structure cristalline, ils prédirent et vérifièrent l'existence de la piézoélectricité sur des cristaux de quartz, de tourmaline, de topaze, de sucre et de sel de Rochelle. L'existence de l'effet inverse fut prédite l'année suivante par Gabriel Lippman sur la base de calculs thermodynamiques[5], et immédiatement vérifiée par les Curie[6]. C'est également en 1881 que Hermann Hankel suggéra l'utilisation du terme piézoélectricité du grec piézein signifiant presser, appuyer[7].
La piézoélectricité resta une curiosité de laboratoire pendant une trentaine d'années ; elle donna surtout lieu à des travaux théoriques sur les structures cristallines présentant cette propriété. Ces travaux aboutirent en 1910 à la publication par Woldemar Voigt du Lehrbuch der Kristallphysik qui donne les vingt classes cristallines piézoélectriques, et définit rigoureusement les constantes piézoélectriques dans le formalisme de l'analyse tensorielle.
D'un point de vue pratique, la piézoélectricité ne fut utilisée que pour réaliser quelques instruments de laboratoire.
Premières applications
La première application de la piézoélectricité fut le sonar développé par Paul Langevin et ses collaborateurs pendant la Première Guerre mondiale. Ce sonar était composé de lames de quartz collées entre deux plaques d'acier et d'un hydrophone et permettait, par la mesure du temps écoulé entre l'émission d'une onde acoustique et la réception de son écho, de calculer la distance à l'objet[8]. Peu de temps après, au début des années 1920, le premier oscillateur à quartz est mis au point par Walter Cady, ouvrant ainsi la voie au contrôle de fréquence[9].
Le succès de ces projets suscita un grand intérêt pour la piézoélectricité, relança les recherches et conduisit à travers les années qui suivirent au développement de nouveaux dispositifs pour une large palette d'applications dans la vie quotidienne, l'industrie et la recherche. L'amélioration du phonographe ou le développement du réflectomètre et du transducteur acoustique, largement utilisé pour les mesures de dureté ou de viscosité, en sont des exemples.
Pendant cette période, les principaux matériaux utilisés sont le quartz, le sel de Seignette et le dihydrogène phosphate de potassium KH2PO4. Or, s'ils peuvent être utilisés, ces matériaux présentent toutefois des inconvénients qui limitent à la fois les applications possibles et l'élaboration de théories de la piézoélectricité.
Découverte des oxydes ferroélectriques
Au cours de la Seconde Guerre mondiale, la recherche de matériaux diélectriques plus performants amena différents groupes de recherche au Japon, aux États-Unis et en Russie à découvrir les propriétés piézoélectriques de céramiques de synthèse composées d'oxydes à structure pérovskite : le titanate de baryum (BaTiO3) puis un peu plus tard les titano-zirconate de plomb (PbZrxTi1-xO3, abrégé en PZT). La mise au point de ces matériaux représente une étape décisive dans le développement des dispositifs piézoélectriques[10]. En effet, leurs propriétés sont globalement bien meilleures ; ils ont des coefficients piézoélectriques de l'ordre de 100 fois supérieurs à ceux des cristaux naturels. Mais surtout, il est possible avec ces céramiques synthétiques de jouer sur différents paramètres de synthèse et ainsi d'ajuster les propriétés du matériau pour une application précise. En particulier, le dopage par divers ions métalliques permet de modifier considérablement leur constante diélectrique, leur dureté, leur usinabilité, etc.
D'un point de vue théorique, ces matériaux constituent également les premiers ferroélectriques simples qui vont permettre d'élaborer et valider les modèles microscopiques.
Un nouveau saut a été effectué au début des années 1980 avec la synthèse des cristaux de PZN-PT et PMN-PT qui présentent les coefficients piézoélectriques les plus élevés connus à ce jour.
Sujets de recherche
Aujourd'hui, les recherches sur les matériaux piézoélectriques portent notamment sur la compréhension précise de ces propriétés exceptionnelles, leur optimisation, ainsi que sur le développement de matériaux sans plomb ou de matériaux utilisables dans une plus large gamme de températures.
Matériaux piézoélectriques
De nombreux cristaux naturels présentent des propriétés piézoélectriques. On peut citer le quartz, la topaze, la tourmaline, la berlinite (AlPO4) ou le sucre. Dans la pratique, les matériaux utilisés pour la fabrication des différents dispositifs sont des matériaux de synthèse qu'on peut classer selon leur structure cristallographique ou leur composition chimique.
Oxydes
 Maille cristalline d'un cristal de structure pérovskite : PbTiO3
Maille cristalline d'un cristal de structure pérovskite : PbTiO3
Les matériaux ferroélectriques de structure pérovskite occupent une large place dans la palette des oxydes piézoélectriques. Ils ont pour formule générale ABO3. On les représente par un empilement d'octaèdres liés par leurs sommets. Les anions oxygène forment les sommets des octaèdres tandis que les cations B et A occupent respectivement leur centre et les sites entre les octaèdres. De nombreux ferroélectriques modèles appartiennent à cette famille : le titanate de plomb PbTiO3, le titanate de baryum BaTiO3, le niobate de potassium KNbO3.
En substituant des cations différents sur les sites A ou B, on peut obtenir des solutions solides. C'est à cette catégorie qu'appartient en particulier le plus couramment utilisé des piézoélectriques, le titano-zirconate de plomb (Pb(ZrxTi1-x)O3 abrégé en PZT), dans lequel les sites B sont occupés par des ions titane et zirconium. On peut également citer des solutions solides entre un relaxeur et le titanate de plomb comme les Pb(Zn1/3Nb2/3)1-xTixO3, Pb(Mg1/3Nb2/3)1-xTixO3, Pb(Sc1/2Nb1/2)1-xTixO3 (abrégés en PZN-xPT, PMN-xPT et PSN-xPT respectivement). C'est dans des cristaux de ce type, pour certaines compositions particulières, que les coefficients piézoélectriques les plus élevés connus sont mesurés.
Le niobate de lithium LiNbO3 et le tantalate de lithium LiTaO3 forment une famille à part. Ils sont tous deux ferroélectriques avec des températures de Curie de 1210°C et 660°C respectivement. Ils ont une structure proche de la maille ilménite de symétrie 3m ; ils n'en diffèrent que par la suite des cations selon leur axe de polarisation (Li-Nb-*-Li-Nb-* contre Fe-Ti-*-Ti-Fe-* pour l'ilménite, où * désigne un site vacant). Ils sont particulièrement utilisés sous forme de monocristaux dans les dispositifs à ondes acoustiques de surface[11].
Certains matériaux de structure cristalline tungstène-bronze sont également utilisés (Ba2NaNb5O5, Pb2KNb5O15). Parmi les autres matériaux piézoélectriques de synthèse, on peut citer l'orthophosphate de gallium (GaPO4), l'arséniate de gallium (GaAsO4) ou les cristaux langasites (dont le langasite de composition La3Ga5SiO14).
Semi-conducteurs
Les semi-conducteurs des groupes III-V de structure zinc-blende et II-VI de structure wurtzite sont également piézoélectriques[12].
Polymères
Il existe également des polymères qui présentent des propriétés piézoélectriques. Les plus couramments utilisés sont des polymères de synthèse, notamment le polyvinylidine difluoride (PVDF) (-CH2-CF2-)n et ses dérivés.
Dans la pratique, les polymères sont utilisés également en couche mince de 6 à 25 microns pour la réalisation de transducteurs ou d'hydrophones. Ils ont l'avantage de présenter une impédance acoustique plus faible, de permettre une mise en forme facile et donc peu onéreuse. En contrepartie, leurs coefficients de couplage électromécanique restent modestes : 12 à 15 % pour le PVDF et jusqu'à 30 % pour le co-polymère P(VDF-TrFE). Ils présentent de plus des pertes diélectriques élevées[13].
Mise en forme
Indépendamment de sa composition chimique, un matériau piézoélectrique peut être étudié et utilisé sous différentes formes. Chacune a des spécificités qui peuvent être mises à profit dans une situation donnée.
Monocristaux
Un monocristal est un arrangement régulier et périodique d'atomes[14]. C'est sous cette forme que se présentent les matériaux piézoélectriques naturels comme le quartz ou la tourmaline, et c'est également sous cette forme qu'ils ont été utilisés dans les applications de première génération avant la mise au point des céramiques.
Les cristaux ferroélectriques peuvent posséder une structure en domaines. On distinguera alors les monocristaux monodomaines et polydomaines selon qu'une ou plusieurs directions de polarisation coexistent dans le cristal. Dans une description cristallographique, les cristaux polydomaines ne sont pas rigoureusement des monocristaux mais des cristaux maclés ; l'usage est cependant de continuer à parler de monocristal.
Les coefficients piézoélectriques les plus élevés connus à ce jour sont obtenus pour des monocristaux polydomaines. Dans la pratique, ils présentent des inconvénients qui limitent leur utilisation dans beaucoup de dispositifs : coût, disponibilité, etc.
Céramiques
Une céramique est composée de grains soudés entre eux par frittage. Les grains sont orientés statistiquement dans toutes les directions ; leur taille peut être contrôlée par les conditions de fabrication.
C'est la forme la plus utilisée, principalement en raison de leur facilité de fabrication et des nombreuses propriétés qu'on peut obtenir en faisant varier la composition chimique, les paramètres de la fabrication, etc.
Si l'on parvient à donner aux grains de la céramique une orientation préférentielle, on obtient alors une céramique texturée dont les propriétés sont en général intermédiaires entre celles d'une céramique et celles d'un monocristal de même composition.
Composites
Dans un composite, le matériau piézoélectrique est divisé et plongé dans une matrice non piézoélectrique (une résine). Les composites ont montré leur intérêt par rapport aux céramiques conventionnelles dans le domaine des transducteurs acoustiques hautes fréquences pour l'imagerie : leur meilleur coefficient de couplage électromécanique et leur impédance acoustique plus adaptée permettent d'améliorer la résolution des images[13].
Couches minces
La piézoélectricité est une propriété à la base des microsystèmes électromécaniques (MEMS) comme les micromoteurs, les microvalves, les accéléromètres ou les membranes. Les avantages des couches minces piézoélectriques sont notamment leur faible puissance de fonctionnement, l'importance des forces générées et les larges gammes de fréquences d'utilisation. Les couches sont en général fabriquées par un procédé sol-gel et ont une épaisseur comprise typiquement entre 0,5 et 5 microns. Le matériau le plus utilisé est là aussi le PZT. Les coefficients piézoélectriques mesurés sur les couches minces sont plus faibles que ceux du matériau massif à cause de l'effet du substrat[15].
Physique macroscopique et formalisme
Dans ce qui suit, on utilisera les notations standard[16]. On notera notamment :
- θ la température et σ l'entropie,
- Tij et Sij le tenseur des contraintes et le tenseur des déformations respectivement,
- Ei et Di le champ électrique et le déplacement électrique respectivement.
De plus, on adopte la convention de sommation d'Einstein.
Approche thermodynamique
Dans une approche thermodynamique, la piézoélectricité est un cas particulier de phénomène de couplage : le couplage entre les phénomènes élastiques et diélectriques d'un système.
Selon les postulats de thermodynamique, on peut caractériser entièrement le système à l'équilibre par la donnée de variables extensives. Il s'agit ici de l'entropie, de la déformation et de la polarisation du système. Ces trois grandeurs sont les variables d'un potentiel thermodynamique dont les caractéristiques du système se déduisent par dérivations successives. Les autres potentiels thermodynamiques, fonctions de variables intensives, sont obtenus du premier par transformation de Legendre. Une présentation des différents potentiels peut être trouvée dans différents ouvrages[17],[18].
Dans ce qui suit, on partira de l'énergie libre de Gibbs[19] qui est uniquement fonction des grandeurs intensives : la température Θ, le champ électrique Ei et les contraintes Tjk. Elle est donnée par[20]
U est l'énergie interne du système, fonction de l'entropie σ, de la déformation S et du déplacement électrique D. La prise en compte de la température n'est pas stricto sensu indispensable à la description thermodynamique de la piézoélectricité : les couplages thermiques étant faibles[21], il n'est généralement pas fait de distinction entre les constantes piézoélectriques isothermes et adiabatiques.
Les constantes piézoélectriques se déduisent du potentiel thermodynamique par dérivée seconde :
L'ordre dans lequel on effectue les deux dérivations est indifférent (c'est le théorème de Schwarz). Selon l'ordre choisi, on fait apparaître deux expressions différentes correspondant aux deux manifestations de l'effet piézoélectrique :
La première expression reflète la variation de polarisation induite par l'application d'une contrainte : c'est l'effet piézoélectrique direct. La seconde indique qu'un champ électrique crée une déformation : c'est l'effet inverse. Ces deux effets sont donc indissociables, et les coefficients associés sont égaux. Dans le système international, on les exprime en mètres par volts m/V ou en coulomb par newton C/N.
L'intégration de ces relations conduit aux équations constitutives de la piézoélectricité. Avec ce choix de potentiel thermodynamique, celles-ci s'écrivent :
Une convention de notation appelée notation de Voigt permet de contracter les indices et de représenter les propriétés électromécaniques sous forme d'une matrice carrée. Les équations constitutives s'écrivent alors sous forme matricielle :
D'autres choix de potentiels thermodynamiques (et donc de variables indépendantes) sont possibles ; il existe donc quatre jeux d'équations constitutives. La représentation pertinente dépend en général des conditions aux limites du problème considéré. Les coefficients piézoélectriques sont alors notés selon les cas e, g ou h. Ces différentes formes des équations de la piézoélectricité sont données dans la norme ANSI/IEEE[16].
Tenseur piézoélectrique
On représente donc la piézoélectricité par un tenseur d'ordre 3, par exemple
Le tenseur piézoélectrique a des propriétés de symétrie qui découlent directement de la symétrie du tenseur des déformations : puisque Sij = Sji, on a également dkij = dkji.
Dans le cas le plus général, il faut 18 coefficients indépendants pour caractériser complètement les propriétés piézoélectriques d'un matériau. Ce nombre est réduit si la structure cristalline du matériau présente des symétries particulières : il n'en faut plus que 4 dans le quartz et 3 dans le titanate de baryum BaTiO3.
Coefficients de couplage électromécanique
Les coefficients de couplage électromécanique sont généralement notés kij. Ils sont compris en 0 et 1 et peuvent être vus comme une sorte de rendement : ils traduisent la faculté d'un matériau piézoélectrique à transformer l'énergie mécanique qu'il reçoit en énergie électrique et inversement[22]. Il s'agit d'une caractéristique essentielle d'un matériau dans la conception de différents dispositifs ; il est notamment relié très directement à la bande passante des transducteurs acoustiques.
On peut définir un coefficient de couplage soit en quasi-statique, soit plus couramment en dynamique dans le cadre de l'étude de la propagation des ondes acoustiques dans le matériau.
Coefficients piézoélectriques complexes
On utilise habituellement les nombres complexes pour rendre compte des phénomènes de dissipation causés par les défauts du milieu. Ainsi, une permittivité complexe permet de représenter les pertes diélectriques d'un milieu, i.e. une faible conductivité. De même, des constantes élastiques complexes permettent de représenter des pertes mécaniques responsables de l'atténuation des ondes acoustiques.
Dans le même esprit, des coefficients piézoélectriques complexes sont parfois utilisés par certains auteurs. Dans bien des cas néanmoins, il est possible de se limiter à des coefficients piézoélectriques réels associés à des constantes diélectriques et élastiques complexes.
Théories et modélisations
Symétries de la maille cristalline
L'existence de la piézoélectricité dans un cristal est liée aux symétries de la maille cristalline. En particulier, un cristal ne peut pas être piézoélectrique si sa maille possède un centre de symétrie (maille dite centrosymétrique).
De manière générale, on classe les cristaux suivant leurs symétries en 230 groupes d'espace regroupés en 32 classes cristallines. Il existe 21 classes non centrosymétriques, dont 20 sont piézoélectriques. Parmi ces classes piézoélectriques, 10 possèdent une polarisation électrique spontanée et sont dites polaires. Leur polarisation spontanée varie avec la température, ces cristaux sont donc pyroélectriques. Parmi les cristaux pyroélectriques enfin, certains sont dits ferroélectriques et se caractérisent par le fait qu'il est possible de renverser leur polarisation électrique permanente en appliquant un fort champ électrique dans le sens opposé.
32 classes cristallines 20 classes piézoélectriques non piézoélectriques 10 classes polaires pyroélectriques non pyroélectriques ferroélectriques non ferroélectriques ex : BaTiO3, PbTiO3 ex : Tourmaline ex : Quartz L'absence de centre de symétrie dans une structure s'explique parfois de manière naturelle par la géométrie. Dans le quartz par exemple, la disposition des ions positifs et négatifs conduit naturellement à la création d'un dipôle électrique lorsque la maille est déformée par une contrainte non hydrostatique. De même, dans les polymères PVDF, la symétrie est naturellement rompue par la substitution de deux atomes d'hydrogène par deux atomes de fluor, beaucoup plus électronégatifs, qui attirent à eux les charges électroniques négatives.
Dans d'autres cas, notamment les ferroélectriques, la brisure de symétrie met en jeu des phénomènes plus complexes. C'est notamment le cas des ferroélectriques modèles qui possèdent à hautes températures une structure cristalline centrosymétrique, non piézoélectrique. À basses températures, la structure de haute symétrie devient instable et le cristal bascule dans une phase de plus basse. L'énergie d'interaction entre dipôles devient prépondérante et favorise le décalage des ions en dehors de leur position de haute symétrie, et l'apparition d'un ordre ferroélectrique à longue portée.
Certains éléments purs cristallisent également dans des structures non centrosymétriques ; c'est le cas du tellure et du sélénium[23]. La brisure de symétrie s'explique dans ce cas par une distorsion de Peierls : les électrons sont localisés en liaisons covalentes de manière dissymétrique autour des atomes.
La symétrie peut également être brisée en moyenne seulement à une échelle de longueur plus grande que celle de la maille cristalline. Ainsi, le silicium n'est pas piézoélectrique, mais un effet piézoélectrique a été mis en évidence dans le silicium poreux[24]. De même, un effet piézoélectrique peut être provoqué par un couplage entre la polarisation et un gradient de déformation (flexoélectricité)[25].
Calculs ab initio
De manière générale, les méthodes ab initio visent à calculer les propriétés d'un matériau à partir de la seule connaissance de sa composition chimique.
Dans le cas des piézoélectriques, la plupart de ces calculs sont réalisés dans le cadre de la théorie de la fonctionnelle densité (DFT) dans l'approximation de la densité locale (LDA)[26]. Ces calculs ont longtemps buté sur plusieurs difficultés spécifiques aux matériaux ferroélectriques. En effet, les approximations classiquement utilisées dans les calculs ab initio sont connues pour introduire des biais qui peuvent fausser l'estimation des volumes. Dans la plupart des matériaux, ces erreurs de quelques pourcents sont insignifiantes, mais pas dans les ferroélectriques, extrêmement sensibles aux variations de volume (ou aux effets de la pression)[26].
Les premiers calculs ab initio de coefficients piézoélectriques ont été publiés en 1989[27] et ont montré que ces théories permettaient de prédire l'apparition de la ferroélectricité.
Modélisation des matériaux hétérogènes
Dans la pratique, les matériaux piézoélectriques sont bien souvent des matériaux hétérogènes (céramiques, composites, monocristaux ferroélectriques polydomaines). La compréhension des propriétés macroscopiques effectives passe par la compréhension du rôle exact de ces multiples interfaces présentes dans le matériau. On introduit alors une distinction entre les contributions intrinsèque et extrinsèque à l'effet piézoélectrique. La contribution intrinsèque désigne l'effet piézoélectrique du matériau considéré comme homogène ; les contributions intrinsèques sont toutes les contributions dues aux interfaces présentes dans la microstructure.
Les contributions extrinsèques sont particulièrement importantes pour les applications : elles sont à l'origine de non-linéarités, de dispersion, de vieillissement qui peuvent être autant de problèmes pour la conception et l'utilisation de dispositifs piézoélectriques[28].
Le problème général est rendu particulièrement ardu par la multiplicité des échelles de longueurs à prendre en compte. Sa résolution nécessite l'adoption d'un certain nombre d'hypothèses simplificatrices. En mécanique, pour les matériaux purement élastiques (non piézoélectrique), ce problème est du domaine de la théorie des milieux effectifs pour laquelle plusieurs méthodes d'homogénéisation ont été développées. Les méthodes classiques (problème d'Eshelby, approximations de Voigt et Reuss) peuvent être étendues aux cas piézoélectriques, mais ne peuvent pas prendre en compte certains effets aux interfaces, notamment la mobilité des parois de domaines.
Les méthodes de calcul par éléments finis, utilisées couramment par ailleurs dans la conception des dispositifs piézoélectriques, peinent à prendre en compte toutes les échelles de longueurs nécessaires dans le cas de matériaux hétérogènes désordonnés. Des méthodes par éléments finis multi-échelles ont cependant été proposées.
On utilise également des méthodes inspirées des méthodes utilisées pour les matériaux composites. Il est ainsi possible de trouver des solutions exactes au problème des structures lamellaires, particulièrement pertinentes dans le cas des ferroélectriques[29].
Ondes acoustiques et résonateurs
La question de la propagation des ondes élastiques dans les milieux piézoélectriques est particulièrement importante dans la mesure où un très grand nombre d'applications de la piézoélectricité en tirent parti.
Dans un piézoélectrique, les propriétés électriques et élastiques étant couplées, il est en principe nécessaire de résoudre le problème en considérant conjointement les équations de l'élasticité et les équations de Maxwell. Le traitement de problème complet est parfois appelé « piézoélectromagnétisme »[30].
Dans la pratique, les ondes acoustiques que l'on considère ont des fréquences inférieures de plusieurs ordres de grandeurs à celles des ondes électromagnétiques. On se contente donc d'une approximation quasi-statique en complétant les équations classiques de l'élasticité par les équations de l'électrostatique. On néglige ainsi le rôle du champ magnétique.
Ondes de volumes
Dans un solide piézoélectrique, la propagation d'une onde élastique de vecteur d'onde n est régie par une équation aux valeurs propres appelée équation de Christoffel[31] :
où les ui sont les composantes du déplacement, ρ est la masse volumique du solide et Γik est la matrice de Christoffel[32]
Afin de retrouver une forme analogue au cas purement élastique, on peut l'écrire :
où les constantes
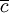 sont appelées constantes élastiques « durcies ». Il faut toutefois prendre garde que ces constantes ne sont pas comparables à de vraies constantes élastiques car elles dépendent de la direction de propagation considérée[33].
sont appelées constantes élastiques « durcies ». Il faut toutefois prendre garde que ces constantes ne sont pas comparables à de vraies constantes élastiques car elles dépendent de la direction de propagation considérée[33].La résolution de l'équation de Christoffel conduit à trois valeurs propres réelles et positives correspondant aux vitesses de propagation de trois ondes. On les obtient en résolvant
Les vecteurs propres correspondants donnent la polarisation des ondes. Celle des trois ondes dont la polarisation est la plus proche de la direction de propagation est dite quasi-longitudinale et les deux autres quasi-transverse. Dans certains cas particuliers, en général le long de directions de haute symétrie, on peut avoir des ondes purement longitudinale (onde de compression) ou purement transverse (onde de cisaillement).
Ondes de surfaces
- Ondes de surfaces, de Bleustein-Gulyaev
Méthodes de mesures et de caractérisation
De manière générale, on entend par caractérisation d'un matériau la détermination d'un certain nombre de ses paramètres permettant d'évaluer sa qualité et son adaptation à une application donnée. On caractérise un matériau piézoélectrique en mesurant notamment ses propriétés électromécaniques, ses coefficients de couplage électromécanique ou son facteur de qualité mécanique selon l'application visée.
Mesures d'impédance complexe
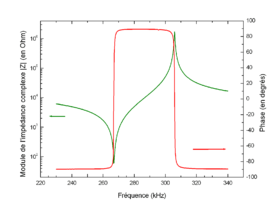
Évolution de l'impédance (module et phase) d'un résonateur piézoélectrique au voisinage de la résonance. Sur cet exemple, la valeur de l'impédance varie sur 4 ordres de grandeurs.
Cette méthode, parfois appelée Méthode IRE[34], est la méthode standard de caractérisation des céramiques piézoélectriques. En mesurant l'impédance complexe de différents échantillons de formes et de dimensions différentes en fonction de la fréquence, on remonte aux différentes caractéristiques du matériau : propriétés électromécaniques, coefficients de couplage, facteurs de qualités mécanique. La procédure est normalisée dans la norme de l'IEEE[16] et décrite au moins partiellement dans les ouvrages de référence[35].
En pratique, on taille plusieurs échantillons de manière à isoler un mode propre de vibration particulier, c'est-à-dire à rejeter les autres modes propres à des fréquences beaucoup plus hautes ou beaucoup plus basses. Au voisinage de la fréquence de ce mode propre, le spectre d'impédance de l'échantillon présente un minimum et un maximum à des fréquences dites de résonance et d'anti-résonance. Ces deux fréquences permettent directement de calculer une constante élastique et un coefficient de couplage électromécanique. En mesurant indépendamment (en général à basses fréquences) la constante diélectrique des échantillons, on peut ensuite calculer un coefficient piézoélectrique. En effectuant cette opération pour plusieurs modes propres de vibration, on peut ainsi déterminer toutes les propriétés du matériau.
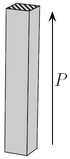
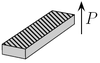
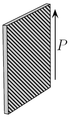
Le tableau suivant présente trois exemples de modes de vibrations utilisés pour la détermination de quelques coefficients de couplage, coefficients piézoélectriques et compliances élastiques d'une céramique ou d'un monocristal piézoélectrique. Dans ce tableau, fM et fm désignent les fréquences où l'impédance est maximale et minimale respectivement[36], L, e et ρ sont la longueur, l'épaisseur et la masse volumique de l'échantillon. La flèche donne la direction de polarisation de l'échantillon ; les électrodes sont représentées par les zones hachurées.
Coeff.
de couplage![k_{33}^2 = \frac{\pi}{2}\frac{f_m}{f_M}\tan\left[\frac{\pi}{2}\left(1-\frac{f_m}{f_M}\right)\right]](/pictures/frwiki/51/3a12bb96cba66a476c46bf4417d16296.png)
Compliance
élastique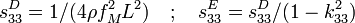
Coeff.
piézoélectrique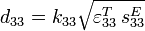
Coeff.
de couplage![\frac{k_{31}^2}{1-k_{31}^2} = \frac{\pi}{2}\frac{f_M}{f_m}\tan\left[\frac{\pi}{2}\left(\frac{f_M}{f_m}-1\right)\right]](/pictures/frwiki/51/385f83a0dad27f008104d02c710cbfcf.png)
Compliance
élastique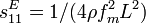
Coeff.
piézoélectrique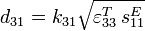
Coeff.
de couplage![k_{15}^2 = \frac{\pi}{2}\frac{f_m}{f_M}\tan\left[\frac{\pi}{2}\left(1-\frac{f_m}{f_M}\right)\right]](/pictures/frwiki/51/31e812136c2f855b6c61c78b8b1a72bc.png)
Compliance
élastique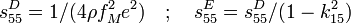
Coeff.
piézoélectrique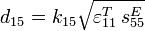
Méthode de Berlincourt
La méthode de Berlincourt, nommée d'après le physicien Don Berlincourt, est une mesure de l'effet piézoélectrique direct. L'échantillon à mesurer est coincé entre deux pièces métalliques et soumis à une contrainte cyclique. Un condensateur est connecté en parallèle, de sorte que le courant produit par l'effet piézoélectrique vient charger le condensateur. Une mesure de la tension aux bornes du condensateur permet de calculer la charge totale et de remonter au coefficient piézoélectrique d33. L'amplitude de la contrainte appliquée est mesurée selon un principe analogue, à l'aide d'un élément piézoélectrique connu placé en série avec l'échantillon.
Cette méthode est rapide, facile à mettre en œuvre et relativement peu onéreuse. Contrairement à la méthode précédente, elle permet d'obtenir le signe du coefficient piézoélectrique d33. Divers appareils sont disponibles dans le commerce. Les modèles les plus élaborés permettent d'étudier les non-linéarités en faisant varier la fréquence ou l'amplitude de la contrainte appliquée.
Les limites de cette technique tiennent à la difficulté de produire dans l'échantillon une contrainte parfaitement homogène. La forme des contacts est importante : un contact en pointe aura tendance à créer des contraintes inhomogènes[37] tandis qu'un contact plat tendra à créer des contraintes latérales à cause des effets de frictions et fera baisser la valeur mesurée[38].
Méthodes non spécifiques
Les deux méthodes de mesures ci-dessus sont spécifiques aux matériaux piézoélectriques. Il est aussi possible de recourir à des méthodes utilisées en mécanique pour la détermination des constantes élastiques. Selon les cas, la généralisation au cas piézoélectrique sera plus ou moins aisée.
Mesures de vitesses d'ondes élastiques
Une façon de déterminer les constantes élastiques et piézoélectriques du matériau est de mesurer les vitesses d'ondes élastiques s'y propageant dans plusieurs directions.
La méthode la plus utilisée consiste à émettre une impulsion sur une face d'un échantillon et de mesurer l'écho de l'onde ainsi créée. La mesure de la durée écoulée entre l'émission de l'onde et son écho permet de mesurer sa vitesse et de là de calculer les constantes élastiques « durcies ». Cette méthode, comme la suivante, nécessite une mesure indépendante des constantes diélectriques du matériau.
Il est également possible de mesurer ces vitesses par diffusion Brillouin. La diffusion Brillouin est la diffusion inélastique de la lumière par les ondes élastiques se propageant dans le cristal. Son utilisation pour la détermination des constantes élastiques est classique pour les matériaux non piézoélectriques[39]. Elle peut être étendue au cas des piézoélectriques ; elle a été notamment utilisée pour la détermination des propriétés de certains piézoélectriques modèles (BaTiO3[40], PbTiO3[41], KNbO3[42]) mais souffre de plusieurs limitations et n'est utilisée qu'à des fins de recherche.
Spectroscopie de résonance acoustique
Article détaillé : Spectroscopie de résonance acoustique.La spectroscopie de résonance acoustique consiste à remonter aux propriétés électromécaniques d'un matériau à partir des fréquences propres de vibration d'un objet. C'est une méthode utilisée couramment en mécanique. Son utilisation pour les matériaux piézoélectriques est plus délicate car le nombre de paramètres à déterminer est plus grand.
Interférométrie laser
Article détaillé : Interférométrie.L'interférométrie laser permet de mesurer directement un déplacement en fonction d'un champ électrique appliqué. Il est possible d'en déduire un coefficient piézoélectrique.
Propriétés de quelques matériaux types
Les coefficients rapportés dans le tableau suivant relient l'allongement d'une barre (sans unité) au champ électrique appliqué entre ses deux extrémités (en V/m). L'unité du système international pour ce coefficient est donc le mètre par volt (m/V). Les indices (33) se rapportent à la direction cristallographique correspondant à la longueur de la barre.
Matériau Coeff. piézo.
d33 (10-12 m/V)Permittivité relative
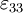
Module d'Young
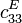 (GPa)
(GPa)Coeff. de couplage
k33 (%)Quartz[43] 2,3 4,5 80 10 BaTiO3 (céramique)[43] 190 1700 106 52 PbTiO3 120 PZT (45/55)[43] 140 450 71 60 PZN-9PT 2500 LiNbO3[44] 6 30 2,45 17 Applications
Transducteurs acoustiques
Article connexe : Transducteur.Les matériaux piézoélectriques permettent de convertir une onde acoustique en signal électrique et inversement. Ils constituent le cœur des transducteurs acoustiques utilisés pour émettre ou détecter des ondes acoustiques dans toutes les gammes de fréquences. On les retrouve dans plusieurs domaines.
- Dans les gammes de fréquences audibles, on réalise des microphones (et en particulier des microphones de contact) et des haut-parleurs, notamment dans les téléphones portables.
- Dans les sonars, utilisés dans la marine, mais aussi dans l'automobile, pour la détection d'obstacles.
- En médecine, on en utilise pour la réalisation d'échographies, qui nécessitent l'émission et la détection d'ondes ultrasonores, ainsi que pour certaines thérapies par ultrasons.
Résonateurs piézoélectriques
Article détaillé : Quartz (électronique).Il est possible de réaliser des résonateurs piézoélectriques très stables (dérivant avec les changements de température et au cours du temps) et avec des fréquences très précises. La vibration piézoélectrique très stable permet de réaliser des références de temps exploitables en électronique. Les montres à quartz utilisent la résonance d'un diapason en quartz pour générer les impulsions régulières d'horloge.
Une caractéristique principale d'un oscillateur est son facteur de qualité qui mesure la finesse de sa résonance mécanique. Il est habituellement noté Q. Les quartz atteignent typiquement des facteurs de qualité de l'ordre de 104 à 106.
Les microbalances piézoélectriques, et particulièrement les microbalances à quartz, reposent également sur ce principe et permettent des mesures de masses très précises.
Capteurs de pression ou d'accélération
Article connexe : Capteur.Une pression exercée sur un matériau piézoélectrique génère des charges que l'on peut mesurer électroniquement. Les matériaux piézoélectriques sont donc des candidats naturels pour les applications basées sur la détection de pressions. Des capteurs de pression piézoélectriques sont utilisés notamment pour l'automobile (pression des pneus), l'aéronautique (pression dans les tuyères) ou la musique (batterie électronique).
Sur le même principe, il est possible de mesurer une accélération. On peut ainsi réaliser des capteurs inertiels (accéléromètre à lame vibrante, gyromètre vibrant Coriolis) qui peuvent être utilisés dans les centrales à inertie ou plus couramment dans des applications de plus basse précision : coussin gonflable de sécurité, guidage, manette de jeu vidéo (wii).
Actionneurs et moteurs piézoélectriques
Les actionneurs et moteurs piézoélectriques tirent profit de l'effet piézoélectrique inverse : dans ces dispositifs, un champ électrique est utilisé pour commander une déformation ou un déplacement. On appelle actionneur piézoélectrique des actionneurs monoblocs contrôlables, utilisant la déformation induite par une tension électrique pour générer le déplacement. Les moteurs piézoélectriques se distinguent des actionneurs en ce qu'ils ne sont pas monoblocs mais composés de plusieurs parties mobiles entre elles.
Actionneurs
Article connexe : Actionneur.Il existe principalement deux types d'actionneurs piézoélectriques :
- les actionneurs directs, dans lesquels le déplacement obtenu est égal à la déformation du matériau piézoélectrique. Les actionneurs directs permettent d'obtenir des courses entre 0 et 100 micromètres.
- les actionneurs amplifiés, dans lesquels un dispositif mécanique vient amplifier ce mouvement, d’un facteur de 2 à 20. Les actionneurs amplifiés ont généralement des courses comprises entre 0,1 mm et 1 mm.
Aujourd'hui, ce sont les céramiques multicouches qui sont traditionnellement utilisées dans les actionneurs piézoélectriques. L'intégration de ce type de matériau impose des précautions spécifiques. On peut citer en particulier la nécessité d'assurer une précontrainte mécanique ou d'éviter les efforts en torsion. Sous réserve d'une bonne conception et utilisation, les actionneurs piézoélectriques sont extrêmement fiables et robustes.
Un des premiers domaines d'application a été le domaine spatial, où leur faible échauffement et leur haute densité énergétique sont des atouts majeurs. Ils sont également utilisés pour le nanopositionnement, la génération de vibrations, le contrôle actif de vibrations[45].
Aujourd'hui, outre le domaine spatial, les actionneurs piézoélectriques sont utilisés dans plusieurs domaines :
- Dans les microscopes à sonde locale. Le microscope à force atomique et le microscope à effet tunnel emploient la piézoélectricité pour réaliser les petits déplacements nécessaires au balayage de la surface sondée ;
- Dans le monde industriel pour de l'assistance à l'usinage par génération de vibrations ;
- Le contrôle de vibrations ;
- La commande de certains injecteurs en automobile est réalisée grâce à des matériaux piézoélectriques. Cette technologie, introduite au début des années 2000, permet notamment de gagner en rapidité d'injection et en consommation[46]. De même, certaines imprimantes à jet d'encre utilisent des éléments piézoélectriques pour produire les fines gouttelettes qui sont propulsées sur le papier ;
- Dans les applications opto-acoustique : par micro-positionnement piézoélectrique de miroir, l'ajustement de la longueur de la cavité laser peut être pilotée pour optimiser la longueur d'onde du faisceau ;
- En optique adaptative en astronomie : des actionneurs piézoélectriques sont utilisés pour déformer un miroir afin de corriger les effets de la turbulence atmosphérique.
Moteurs piézoélectriques
Article détaillé : Moteur piézoélectrique.Les moteurs piézoélectriques sont utilisés dans les systèmes autofocus d'appareils photographiques, dans les mécanismes de vitre électrique de voiture, et en général dans les applications où la taille réduite de ces moteurs répond à des contraintes volumiques[47].
Générateurs et transformateurs
L'allume-gaz et le briquet « électronique » sont des exemples de la manière dont les piézoélectriques permettent de produire de fortes tensions. L'effet piézoélectrique direct permet de générer de très fortes tensions, supérieures à la tension de claquage de l'air 30 kV/cm pour un écartement de quelques millimètres. Lorsque cette tension est atteinte, une étincelle de décharge est produite et mise à profit pour allumer le gaz du briquet ou de la gazinière.
Transformateurs piézoélectriques
Un transformateur piézoélectrique est un multiplicateur de tension alternative. Contrairement au transformateur classique qui utilise un couplage magnétique, le couplage mis à profit est acoustique. Par effet piézoélectrique inverse, une tension d'excitation permet de générer (à l'aide d'électrodes situées sur une des deux extrémités de la barre) une contrainte alternative dans une barre d'un matériau fortement piézoélectrique (une céramique PZT par exemple). Cette contrainte permet la mise en vibration de la barre à une fréquence choisie pour correspondre à une fréquence de résonance. Par effet piézoélectrique direct, une tension est générée sur des électrodes situées sur la deuxième extrémité de la barre. Cette tension, qui bénéficie de l'amplification du mouvement dû à la résonance, peut être 1 000 fois plus élevée.
Microgénérateurs
Les piézoélectriques sont aussi au cœur d'applications plus récentes visant à récupérer l'énergie présente dans notre environnement sous différentes formes ou effectuées par des mouvements quotidiens[48].
Un exemple étudié en laboratoire est l'incorporation d'un film piézoélectrique dans les chaussures afin de produire de l'énergie grâce à la pression du talon pendant la marche. Les faibles puissances produites pourraient suffire à terme à alimenter certains dispositifs électroniques. Toutefois, la mise au point de tels dispositifs piézoélectriques reste délicate et de nombreux obstacles restent à surmonter.
Les premiers produits, dit microgénérateurs, sont apparus en 2006[réf. nécessaire]. Ils récupèrent par exemple l'énergie mécanique fournie par la pression du doigt sur un bouton. L'électricité ainsi récupérée sert à alimenter un circuit radio, qui émet un message. Ce principe est utilisé pour fabriquer des sonnettes de maison. Il existe des applications plus techniques comme les réseaux de capteurs sans fil où la source d'énergie est la vibration. Les applications sont la maintenance préventive, ou le contrôle de processus.
Filtres
Il est possible de mettre à profit les résonances mécaniques d'échantillons pour réaliser des filtres en électronique[49].
Les filtres à ondes acoustiques de surface (filtres SAW) quant à eux utilisent les propriétés de propagation des ondes à la surface du matériau.
Microscopie à force piézoélectrique (PFM)
La microscopie à force piézoélectrique (en anglais piezoresponse force microscopy - PFM) est un mode particulier d'utilisation du microscope à force atomique : l'application d'une tension entre la pointe et l'échantillon permet de sonder la structure en domaines ferroélectriques à l'échelle nanométrique[50].
Notes et références
- ↑ Antoine-César Becquerel, « Expériences sur le développement de l'électricité par la pression ; lois de ce développement », dans Annales de chimie et de physique, vol. XXII, 1823, p. 5-34
- ↑ Antoine-César Becquerel, « De quelques phénomènes électriques produits par la pression et le clivage des métaux », dans Annales de chimie et de physique, vol. XXXVI, 1827, p. 265-271
- ↑ Voir l'introduction aux leçons de René Just Haüy dansÉtienne Guyon et , Leçons de physique, de chimie et d'histoire naturelle, Éditions Rue d'Ulm, coll. « L'École normale de l'an III », Paris, 2006
- ↑ Christine Blondel, « Haüy et l'électricité : de la démonstration spectacle à la diffusion d'une science newtonienne », dans Revue d'histoire des sciences, vol. 50, 1997, p. 265-282 [texte intégral]
- ↑ G. Lippman, « Principe de la conservation de l'électricité », dans Annales de chimie et de physique, vol. 24, 1881, p. 145 [texte intégral]
- ↑ P. Curie et J. Curie, « Contractions et dilatations produites par des tensions électriques dans les cristaux hémièdres à faces inclinées », dans Comptes rendus de l'Académie des Sciences, vol. XCIII, séance du 26 décembre 1881, p. 1137 [texte intégral]
- ↑ (de) F. Pockels, Pyro- und piezoelektrizität, Elektrizität und Magnetismus I (Handbuch der Physik vol 4), Dr A Winkelmann, Leipzig, 1905, p. 766–93
- ↑ (en) Warren P. Mason, « Piezoelectricity, its history and applications », dans Journal of the Acoustical Society of America, vol. 70, no 6, 1981, p. 1561
- ↑ (en) Arthur Ballato, « Piezoelectricity: Old Effect, New Thrusts », dans IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 42, 1995, p. 916
- ↑ Une histoire de la piézoélectricité
- ↑ Ikeda, 1996, p. 218-219
- ↑ (en) Fred S. Hickernell, « The Piezoelectric Semiconductor and Acoustoelectronic Device Development in the Sixties », dans IEEE Transactions on ultrasonics, ferroelectrics, and frequency control, vol. 52, 2005, p. 737 [texte intégral]
- ↑ a et b (en) Shung KK, Cannata JM, Zhou QF, « Piezoelectric materials for high frequency medical imaging applications: A review », dans Journal of Electroceramics, vol. 19, 2007, p. 139-145
- ↑ Voir Cristal pour une définition plus rigoureuse.
- ↑ (en) N. Setter et al., « Ferroelectric thin films: Review of materials, properties and applications », dans Journal of Applied Physics, vol. 100, 2006, p. 051606
- ↑ a , b et c (en)ANSI/IEEE Standard on Piezoelectricity, 1996 [détail des éditions]
- ↑ Ikeda 1996, chap 2
- ↑ Lines & Glass, 1977
- ↑ Il n'existe pas vraiment de termes bien identifiés pour désigner les potentiels thermodynamiques dans le cas des milieux diélectriques.
- ↑ Ikeda, p. 11
- ↑ Ikeda, p. 15
- ↑ Éléments d'explications sur les coefficients de couplage électromécanique
- ↑ (en) D. Royer and E. Dieulesaint, « Elastic and piezoelectric constants of trigonal selenium and tellurium crystals », dans Journal of Applied Physics, vol. 50, 1979, p. 4042 [texte intégral]
- ↑ (en) S. Vinikman-Pinasy, E.N. Ribak, « Piezoelectric and piezooptic effects in porous silicon », dans Applied Physics Letters, vol. 88, 2006, p. 111905
- ↑ (en) J. Fousek, L.E. Cross, D.B. Litvin, « Possible piezoelectric composites based on flexoelectric effect », dans Materials Letters, vol. 39, 1999, p. 259
- ↑ a et b R.E. Cohen, « First-Principles Theories of Piezoelectric Materials » dans Piezoelectricity (2008)
- ↑ (en) K. M. Rabe, C. H. Ahn et J.-M. Triscone et R. Resta et D. Vanderbilt, Physics of Ferroelectrics - A Modern Perspective, Springer, 2007 (ISBN 978-3-540-34590-9), « Theory of Polarization: A Modern Approach », p. 31-68
- ↑ (en) Dragan Damjanovic, « Contribution to the piezoelectric effect in ferroelectric single crystals and ceramics », dans Journal of the American Ceramic Society, vol. 88, 2005, p. 2663-2676
- ↑ W. Kreher, « Effective Medium Theories » dans Piezoelectricity (2008).
- ↑ (en) Jiashi Yang, « A Review of a Few Topics in Piezoelectricity », dans Applied Mechanics Reviews, vol. 59, 2006, p. 335-345
- ↑ Dieulesaint & Royer
- ↑ Dieulesaint & Royer
- ↑ Dieulesaint & Royer
- ↑ en référence à la première normalisation qui en fut donnée par l'IRE : (en) « IRE Standards on Piezoelectric Crystals », dans Proceedings of the IRE, 1961, p. 1162-1169
- ↑ Diverses présentations sont également disponibles en ligne, voir par exemple : (en) Procedures for Measuring Properties of Piezoelectric Ceramics ou Article disponible sur arXiv : 0711.2657. (en).
- ↑ Travailler avec les maximum et minimum de l'impédance | Z | n'est possible que si les pertes sont négligeables. Dans le cas contraire, il faut définir plus précisément les fréquences caractéristiques du système.
- ↑ (en) J. Erhart and L. Burianova, « What is really measured on a d33-meter ? », dans Journal of the European Ceramic Society, vol. 21, 2001, p. 1413-1415
- ↑ (en) A. Barzegar, D. Damjanovic, and N. Setter, « The effect of boundary conditions and sample aspect ratio on apparent d33 piezoelectric coefficient determined by direct quasistatic method », dans IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, vol. 51, 2003, p. 262-270
- ↑ (en) R. Vacher et L. Boyer, « Brillouin Scattering: A Tool for the Measurement of Elastic and Photoelastic Constants », dans Physical Review B, vol. 6, 1972, p. 639
- ↑ (en) Z. Li, S. K. Chan, M. H. Grimsditch, E. S. Zouboulis, « The elastic and electromechanical properties of tetragonal BaTiO3 single crystals », dans Journal of Applied Phyics, vol. 70, 1991, p. 7327
- ↑ (en) A. G. Kalinichev, J. D. Bass, B. N. Sun, D. A. Payne, « Elastic properties of tetragonal PbTiO3 single crystals by Brillouin scattering », dans Journal of Materials Research, vol. 12, 1997, p. 2623
- ↑ (en) A. G. Kalinichev, J. D. Bass, C. S. Zha, P. Han, D. A. Payne, « Elastic properties of Orthorhombic KNbO3 single crystals by Brillouin scattering », dans Journal of Applied Physics, vol. 74, 1993, p. 6603
- ↑ a , b et c Piezoelectricity sur le site de Morgan Electroceramics.
- ↑ Ikeda 1996, p. 220
- ↑ Exemples de publications sur les actionneurs piézoélectriques
- ↑ Auto-innovations : actualité moteur et transmission
- ↑ Moteurs piézoélectriques par Bertrand Nogarede sur Techniques de l'ingénieur.
- ↑ (en) S. R. Anton, H. A. Sodano, « A review of power harvesting using piezoelectric materials (2003-2006) », dans Smart Materials and Structures, vol. 16, 2007, p. R1-R21
- ↑ (en) Description de filtres à base de céramiques piézoélectriques
- ↑ A. Gruverman and S. V. Kalilin, Piezoresponse force microscopy and recent advances in nanoscale studies of ferroelectrics, Journal of Material Sciences 41, 107-116 (2006).
(en) Cet article est partiellement ou en totalité issu d’une traduction de l’article en anglais intitulé « Piezoelectricity ».
Voir aussi
Articles connexes
Bibliographie
- (fr) John Frederick Nye, Propriétés physiques des cristaux [« Physical Properties of Crystals »], 1961 [détail des éditions]
- (fr) E Dieulesaint, D Royer, Ondes élastiques dans les solides - Application au traitement du signal, Masson et Cie, 1974.
Le contenu de cet ouvrage est partiellement repris par les mêmes auteurs dans Propagation et génération des ondes élastiques, 2001, Techniques de l'ingénieur.
- (en) Warren P. Mason, Piezoelectric Crystals and their Application to Ultrasonics, Van Nostrand, New York, 1950
- (en) M.E. Lines and A.M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Oxford University Press, 1977
- (en) Takuro Ikeda, Fundamentals of Piezoelectricity, Oxford University Press, 1996 (ISBN 0-19-856339-6)
- (en) Shaul Katzir, The Beginnings of Piezoelectricity: A Study in Mundane Physics, Springer, 2006 (ISBN 1402046693).
Cet ouvrage est issu du mémoire de doctorat de l'auteur. Certaines parties ont été publiées indépendamment dans des revues : « The Discovery of the Piezoelectric Effect », dans Archive for the history of exact sciences, vol. 57, 2003, p. 61-91 [texte intégral]
- (en) W. Heywang, Karl Lubitz et Wolfram Wersing et , Piezoelectricity, Springer, 2008 (ISBN 978-3-540-68680-4)
Liens externes
- (en) Une histoire de la piézoélectricité. Consulté le 14/11/08
- Portail de la physique
- Portail de l’électricité et de l’électronique
Catégories : Électricité | Physique du solide
Wikimedia Foundation. 2010.


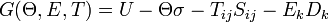
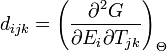
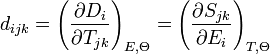
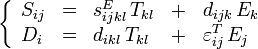
![\left[\begin{array}{l}S_{\alpha} \\ D_i \end{array}\right]
=
\left[\begin{array}{c|c}s_{\alpha\beta}^E & d_{\alpha j} \\\hline d_{i\beta} & \varepsilon_{ij}^T \end{array}\right]
\left[\begin{array}{l}T_{\beta} \\ E_j \end{array}\right]](/pictures/frwiki/101/e0f1fba76626ea73b69080525fd20fa0.png)