Filtre (electronique)

Un filtre est un circuit électronique qui réalise une opération de traitement du signal. Autrement dit, il atténue certaines composantes d'un signal et en laisse passer d'autres. Un exemple connu du grand public est l'égaliseur audio.

Un filtre modifie (ou filtre) certaines parties d'un signal d'entrée dans le domaine temps et dans le domaine fréquence. D'après la théorie de Fourier, tout signal réel peut être considéré comme composé d'une somme de signaux sinusoïdaux (en nombre infini si nécessaire) à des fréquences différentes ; le rôle du filtre est de modifier la phase et l'amplitude de ces composantes.

Sommaire 1 Définition 1.1 Filtre linéaire 1.2 Filtre non-linéaire 2 Historique 3 Classification 3.1 Classification par type 3.2 Classification par technologie 3.2.1 Filtre passif 3.2.2 Filtre actif 3.2.3 Filtre numérique 3.3 Classification par spécificités 3.3.1 Filtre à capacités commutées 3.3.2 Filtre piézoélectrique 3.3.3 Filtre SAW 3.3.4 Filtre céramique 3.3.5 Filtre atomique 4 Stabilité 5 Synthèse 6 Applications 7 Bibliographie 8 Notes 9 Voir aussi 9.1 Articles connexes

Définition

Filtre linéaire

Un filtre linéaire est caractérisé par l'existence d'une fonction h(t) telle que la réponse du filtre à tout signal d'entrée e(t) soit:

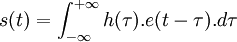
Il s'agit bien du produit de convolution des fonctions h et e que l'on peut aussi noter :

s = h * e

h est appelée la réponse impulsionnelle du filtre. La connaitre permet de caractériser totalement le filtre.

Filtre non-linéaire

Historique

Classification

Classification par type

On peut classer les filtres à partir de la forme de leur fonction de transfert ou par le comportement des élements passifs qui composent le filtre. Les filtres les plus courants sont de l'un des quatre types suivants : passe-bas, passe-haut, passe-bande ou réjecteur de bande.

• Un filtre passe-haut ne laisse passer que les fréquences au-dessus d'une fréquence déterminée, appelée fréquence de coupure. Il atténue les autres (basses fréquences). Autrement dit, il « laisse passer ce qui est haut ». C'est un atténuateur de graves pour un signal audio. On pourrait aussi l'appeler coupe-bas.
• Un filtre passe-bas ne laisse passer que les fréquences au-dessous de sa fréquence de coupure. C'est un atténuateur d'aigües pour un signal audio. On pourrait l'appeler coupe-haut.
• Un filtre passe-bande ne laisse passer qu'une certaine bande de fréquences (et atténue tout ce qui est au-dessus ou en dessous). Il est très utilisé dans les récepteurs radio, TV… pour isoler le signal que l'on désire capter.
• Un filtre réjecteur, aussi appelé filtre trappe, cloche ou coupe-bande, est le complémentaire du passe-bande. Il atténue une plage de fréquences. Cela peut être utile pour diminuer certains parasites par exemple.
• Un filtre passe-tout, également appelé filtre déphaseur ou cellule correctrice de phase, est un filtre qui a idéalement un gain unitaire sur toute la plage de fréquence utilisée. Il est utilisé pour modifier la phase d'un système.

Résultat de l'application d'un filtre passe-bas sur une image

Résultat de l'application d'un filtre passe-haut sur une image

Résultat de l'application d'un filtre passe-bande sur une image

Cliquez sur une vignette pour l’agrandir

Classification par technologie

Filtre passif

Un filtre passif se caractérise par l'usage exclusif de composants passifs (résistances, condensateurs, bobines couplées ou non). Par conséquent, leur gain (rapport de puissance entre la sortie et l'entrée) ne peut excéder 1. Autrement dit, ils ne peuvent qu'atténuer en partie des signaux, mais pas les amplifier car cela nécessiterait un apport d'énergie.

Les réalisations les plus simples sont basées sur des circuits RC, RL, LC ou Circuit RLC. Mais il est bien sûr permis d'augmenter la complexité du filtre (et le nombre de composants). Moins il y aura de composants, plus il sera délicat d'être sélectif : l'atténuation se fera progressivement. Avec plus de composants, on peut espérer couper plus brutalement une fréquence en touchant moins les voisines.

Les filtres passifs sont rarement sujets à des phénomènes de saturation (hormis quelques cas de bobines avec noyau) d'où par exemple leur usage dans les enceintes de haut-parleurs. De plus ils peuvent exister dans toutes les gammes de fréquences (d'où leur usage dans certains circuits haute fréquence comme en radio par exemple). Toutefois, un même circuit peut difficilement couvrir à lui seul une très large gamme de fréquences car le choix d'un type de bobine ou de condensateur dépend de la fréquence. C'est faisable mais plus complexe. Citons l'exemple du condensateur électrochimique : bien adapté aux basses fréquences, il devient assez vite inductif avec l'augmentation de la fréquence (il perd son comportement capacitif).

Une bobine est constituée d'un fil et est donc très conductrice en basse fréquence. Par contre, elle s'oppose au passage des hautes fréquences. Les condensateurs font l'inverse (isolant en basse fréquence, conducteur en haute fréquence). Les résistances ne sélectionnent pas les fréquences à elles seules, mais permettent de définir les constantes de temps d'un circuit en limitant plus ou moins les courants. Donc les résistances déterminent la fréquence à laquelle le filtre agira et son atténuation.

Au-delà de 100 MHz : les inductances sont souvent constituées par un simple fil sinueux ou des bandes de métal, et les condensateurs par des bandes de métal superposées (stubs). Par exemple sur les deux faces opposées d'un circuit imprimé.

Pour les filtres du second ordre, c'est-à-dire pouvant être décrits par une équation différentielle (linéaire très souvent) du second ordre, il est possible de définir un facteur de qualité, c’est-à-dire le rapport entre leur fréquence centrale et leur bande passante , attention ceci n'est valable que pour un passe-bande. Un filtre ayant une bande très fine par rapport à sa fréquence centrale sera considéré comme très sélectif ou de grande qualité.

Le circuit est soumis à plus ou moins de bruits parasites apparaissant dans les signaux. Cela dépend des composants employés. Bruit thermique très faible dans les résistances, bruit assez faible dans les condensateurs, mais sensibilité aux champs magnétiques plus importante avec les bobines.

Pour être complet, il convient de mentionner les filtres à quartz, les filtres à onde de surface (Surface Acoustic Waves filters ou SAW), les filtres céramique et les filtres mécaniques, qui font aussi partie des filtres passifs.
Ils peuvent être considérés dans le cas le plus général comme des quadripoles.

Filtre actif

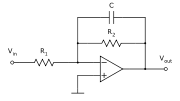
Les filtres actifs se caractérisent par l'usage d'au moins un composant actif (par exemple transistor, amplificateur opérationnel, ou autre circuit intégré…).

Ces filtres ont l'avantage de pouvoir se passer de bobines qui sont chères, difficilement miniaturisables et imparfaites (angles de pertes, résonances propres, sensibilité aux parasites). De plus ils ont un gain qui peut être supérieur à 1 (ils peuvent amplifier).

Ce type de filtre convient bien aux signaux de faible amplitude et de faible puissance. Les filtres actifs sont donc largement utilisés dans les amplificateurs audio et instruments électroniques de toutes sortes.

Côté inconvénients, contrairement aux filtres passifs, ils nécessitent une alimentation électrique et sont limités en amplitude (saturation). Aujourd'hui ils peuvent couvrir de larges bandes de fréquences. Les composants actifs (ainsi que les résistances dans une moindre mesure) peuvent introduire du bruit parasite, ce qui, au-delà d'un certain seuil, peut être gênant. Toutefois ce bruit peut souvent être maîtrisé.

Filtre numérique

Un filtre numérique se caractérise par le traitement entièrement numérique du signal. Au préalable, le signal analogique est filtré par un filtre antirepliement puis il est numérisé par un convertisseur analogique-numérique (CAN) qui généralement intègre un échantillonneur-bloqueur, c’est-à-dire qu’à intervalles réguliers (appelés période d’échantillonnage), l’amplitude instantanée du signal est échantillonnée et maintenue puis quantifiée. On n’observe donc pas le signal en permanence et ces filtres réagissent donc assez mal face à des signaux (même parasites) de fréquence plus élevée que celle prévue (en l'absence de filtre anti-repliement).

Un filtre numérique traite un flot continu d'informations (comme par exemple celui d'une caméra vidéo) et calcule en temps réel un nouveau flot de données sortantes, qui correspondent au signal filtré désiré. Les données de sortie peuvent apparaître au même rythme ou à un rythme différent des données entrantes.

En bout de chaîne, le signal analogique est reconstruit par un convertisseur numérique-analogique (CNA) suivi d'un filtre de lissage. Les filtres numériques ont l’avantage de pouvoir être intégrés dans des circuits numériques miniaturisables à l’extrême, tels des processeurs (Digital Signal Processors, DSP en particulier). Les filtres analogiques ne sont pas supprimés pour autant (anti-repliement et lissage).

Les caractériques du filtre numérique sont invariable dans le temps, mais cela ne garanti pas que les caractériques d'un appareil qui en utilise seront invariables. Les CNA et CAN ne sont jamais parfaits et leurs caractériques varient d'un lot de composants à l'autre. Même si l'appareil ne possède pas de convertisseur (il reçoit une information numérique, la filtre puis la transmet en numérique) alors se pose le problème de la gigue d'horloge (les oscillateurs ne sont jamais parfaits) et de la synchronisation des données. Autre fait important, il existe deux types de filtre :

• les filtre à réponse impulsionnelle finie (RIF),
• les filtre à réponse impulsionnelle infinie (RII).

Si les premiers sont toujours stables, ce n'est pas le cas pour les seconds.

Toutefois, les filtres numériques ont évidemment des limitations (arrondis de calcul, amplitude limitée, repliement de spectre…). Par contre ils offrent l’avantage de pouvoir être reprogrammés (éventuellement à la volée) pour changer de caractéristiques rapidement, sans changer de circuit matériel (sauf si le filtre numérique est réalisé par un ASIC).

Ils permettent d’obtenir des caractéristiques spectrales dont certaines ne peuvent être reproduites par aucun filtre analogique (actif ou non) : par exemple, ils peuvent être très sélectifs ou éliminer toute une série de composantes harmoniques (filtre en peigne). C’est uniquement une question de calcul mathématique.

La fréquence maximale du spectre du signal que traite un filtre numérique doit rester bien inférieure à la moitié de la fréquence d'échantillonnage (Théorème d'échantillonnage de Nyquist-Shannon), et que par conséquent le filtre numérique n'est pas adapté pour des signaux étalés sur une trop grande bande de fréquences. Il a fallu attendre la montée en puissance des capacités de calcul des processeurs pour voir apparaître ces filtres à grande échelle. Ils sont dorénavant très utilisés dans l’électronique moderne où l’analogique cède le pas au numérique. La plupart des signaux étant numériques ils sont traités directement comme tels.

Classification par spécificités

Filtre à capacités commutées

Les circuits à capacités commutées peuvent être utilisées pour la réalisation de filtres analogiques. Ils permettent une meilleure intégration, et un réglage aisé des fréquences de coupure.

Filtre piézoélectrique

Les qualités piézoélectriques de certains matériaux, comme le quartz, peuvent être utilisées dans la conception de filtres. Les filtres à quartz possèdent un facteur de qualité élevé et une très bonne stabilité en température.

Filtre SAW

Un filtre SAW (de l'anglais Surface Acoustic Wave, « onde acoustique de surface ») est un système électromécanique utilisé généralement dans des applications utilisant les ondes radio. Les signaux électriques sont convertis en onde mécanique par un cristal piézoélectrique. Cette onde est retardée lors de sa propagation dans le cristal, puis reconvertie en signal électrique. Les sorties retardées sont recombinées pour produire une implémentation d'un filtre à réponse impulsionnelle finie.

Filtre céramique

Filtre atomique

Pour des fréquences et une précision plus élevées, il est possible d'utiliser les modes vibratoires d'atomes. Les horloges atomiques utilisent des masers à césium comme filtres à très haut facteur de qualité afin de stabiliser leurs oscillateurs primaires. Une autre méthode, utilisée pour des fréquences élevées et fixes sur des signaux radio très faibles, est d'utiliser un laser à rubis.

Stabilité

Synthèse

La synthèse de filtres linéaires représente l'ensemble des outils mathématiques destinés à concevoir un filtre à partir de spécifications dans le domaine fréquentiel et/ou temporel.

Applications

Tous les produits électroniques utilisent des filtres. On peut néanmoins citer dans le domaine des :

• Télécommunications
  • Poste radio : sélection de la fréquence de chaque station émettrice.
  • Télévision : sélection des chaînes de télévision ou canaux.
  • Téléphone à touches : chaque touche envoie un signal de 2 fréquences précises qui « signent » un chiffre; avec 10 chiffres, on compose le numéro d'appel de son correspondant
  • ADSL : sur la même ligne téléphonique peuvent passer tout à la fois une conversation téléphonique BF ( basse fréquence: typiquement les fréquences audibles), le signal d'une chaîne télé (HF large bande), et le signal du IP (InternetProtocol). Voir Filtre ADSL et Filtre ADSL ISDN
• Audio
  • Filtres utilisés en sonorisation

Bibliographie

Annales des Télécommunications, édition Springer Paris (francais)

Notes

Voir aussi

Articles connexes

• Bande passante
• Diagramme de Bode
• Fréquence de coupure

Électromagnétisme | Électricité | Électronique | Électrotechnique | Électrochimie | Automatique | Traitement du signal

Types de filtres : Filtre passe-bas · Filtre passe-haut · Filtre passe-bande · Filtre coupe-bande

filtres linéaires : Filtre de Bessel · Filtre de Butterworth · Filtre de Tchebychev · Filtre elliptique

filtres numériques : Filtre à réponse impulsionnelle finie · Filtre à réponse impulsionnelle infinie

• Portail de l’électricité et de l’électronique