Macle (cristallographie)

Pour les articles homonymes, voir Macle.

Macle par pénétration de trois cristaux de pyrite

Une macle est une association orientée de deux ou plusieurs cristaux identiques, dits individus, reliés par une opération de groupe ponctuel de symétrie.

Sommaire

1 Propriétés des macles
- 1.1 Indice d'une macle
- 1.2 Obliquité d'une macle
2 Classification des macles
3 Exemples de macles
4 Galerie
5 Notes et références
6 Voir aussi

Propriétés des macles

Indice d'une macle

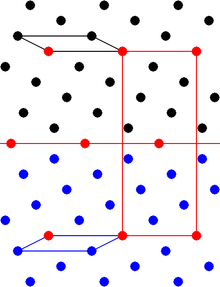Exemple de réseau de macle bidimensionnel. Les réseaux noir et bleu sont deux individus de la macle. Leurs mailles primitives sont les parallélogrammes noir et bleu. Les nœuds communs aux deux réseaux sont marqués en rouge. L'élément de la macle est représenté par la ligne rouge. La maille primitive du réseau de la macle est le rectangle rouge (malgré les apparences, dans cette figure, la maille du réseau de la macle n'est pas centrée).

Les cristaux formant une macle ont en commun un réseau qui s'appelle réseau de la macle. Ce réseau est formé par les nœuds des réseaux des individus maclés qui sont superposés par l'opération de macle. Selon que ce réseau existe en une, deux ou trois dimensions, les macles sont dites monopériodiques, dipériodiques et tripériodiques respectivement. La plupart des macles sont tripériodiques.

Le rapport entre le volume de la maille primitive de la macle et celui de la maille primitive de l'individu constitue l'indice de la macle $n$ et correspond à l'inverse de la fraction de nœuds superposés par l'opération de macle. Soit $(h k l)$ le plan de macle et $[u v w]$ la direction réticulaire (quasi)-perpendiculaire à $(h k l)$ . Ou encore, soit $[u v w]$ l'axe de macle et $(h k l)$ le plan réticulaire (quasi)-perpendiculaire à $[u v w]$ . Pour une macle binaire (où l'opération de macle est d'ordre 2, c'est-à-dire une rotation de 180° autour d'une direction réticulaire ou une réflexion par rapport à un plan réticulaire), l'indice de macle est calculé d'après la formule suivante :

$n = \frac{|uh+vk+wl|}{f} = \frac{X}{f}$

où $f$ dépend du type de réseau et de la parité de $X$ , $h$ , $k$ , $l$ , $u$ , $v$ et $w$ , comme dans le tableau suivant.

Type de réseau	Conditions sur $h k l$	Conditions sur $u v w$	Conditions sur $X$	$n$
P	aucune	aucune	$X$ impair	$n = X$
P	aucune	aucune	$X$ pair	$n = X / 2$
C	$h + k$ impair	aucune	aucune	$n = X$
	$h + k$ pair	$u + v$ et $w$ de parités différentes	$X$ impair	$n = X$
		$u + v$ et $w$ de parités différentes	$X$ pair	$n = X / 2$
		$u + v$ et $w$ pairs	$X / 2$ impair	$n = X / 2$
		$u + v$ et $w$ pairs	$X / 2$ pair	$n = X / 4$
B	$h + l$ impair	aucune	aucune	$n = X$
	$h + l$ pair	$u + w$ et $v$ de parités différentes	$X$ impair	$n = X$
		$u + w$ et $v$ de parités différentes	$X$ pair	$n = X / 2$
		$u + w$ et $v$ pairs	$X / 2$ impair	$n = X / 2$
		$u + w$ et $v$ pairs	$X / 2$ pair	$n = X / 4$
A	$k + l$ impair	aucune	aucune	$n = X$
	$k + l$ pair	$v + w$ et $u$ de parités différentes	$X$ impair	$n = X$
		$v + w$ et $u$ de parités différentes	$X$ pair	$n = X / 2$
		$v + w$ et $u$ pairs	$X / 2$ impair	$n = X / 2$
		$v + w$ et $u$ pairs	$X / 2$ pair	$n = X / 4$
I	$h + k + l$ impair	aucune	aucune	$n = X$
	$h + k + l$ pair	$u$ , $v$ et $w$ de parités différentes	$X$ impair	$n = X$
		$u$ , $v$ et $w$ de parités différentes	$X$ pair	$n = X / 2$
		$u$ , $v$ et $w$ impairs	$X / 2$ impair	$n = X / 2$
		$u$ , $v$ et $w$ impairs	$X / 2$ pair	$n = X / 4$
F	aucune	$u + v + w$ impair	aucune	$n = X$
	$h$ , $k$ , $l$ de parités différentes	$u + v + w$ pair	$X$ impair	$n = X$
	$h$ , $k$ , $l$ de parités différentes	$u + v + w$ pair	$X$ pair	$n = X / 2$
	$h$ , $k$ , $l$ impairs	$u + v + w$ pair	$X / 2$ impair	$n = X / 2$
	$h$ , $k$ , $l$ impairs	$u + v + w$ pair	$X / 2$ pair	$n = X / 4$

Obliquité d'une macle

Dans les macles par réflexion, le plan de macle est perpendiculaire à une rangée du réseau de la macle. Dans les macles par rotation, l'axe de macle est perpendiculaire à un plan du réseau de la macle. Toutefois, cette perpendicularité peut être seulement approximative, la déviation de la perpendicularité exacte étant mesurée par un angle ω dit obliquité. Le concept d'obliquité fut introduit par Georges Friedel en 1920 comme mesure de la superposition des réseaux des individus formant une macle.

Soit $[u' v' w']$ la direction exactement perpendiculaire au plan de macle $(h k l)$ , et soit $(h' k' l')$ le plan exactement perpendiculaire à l'axe de macle $[u v w]$ . $[u' v' w']$ est parallèle au vecteur du réseau réciproque $[h k l] *$ et $(h' k' l')$ est parallèle au plan du réseau reciproque $[u v w] *$ . L'angle entre $[u v w]$ et $[u' v' w']$ , qui est le même que celui entre $(h k l)$ et $(h' k' l')$ , est l'obliquité ω.

Le vecteur de l'espace direct $[u v w]$ a pour norme $L (u v w)$ ; le vecteur du réseau réciproque $[h k l] *$ a pour norme $L * (h k l)$ . L'obliquité ω est l'angle entre les deux vecteurs $[u v w]$ et $[h k l] *$ . Le produit scalaire de ces deux vecteurs est :

$L(uvw) \cdot L^*(hkl) \cdot \cos{\omega} = <uvw|hkl> = uh+vk+wl$

où <| signifie matrice ligne 1x3 et |> signifie matrice colonne 3x1. Par conséquent :

$\cos{\omega} = \frac{uh+vk+wl}{L(uvw) \cdot L^*(hkl)}$

où

$L(uvw) = \sqrt{<uvw|G|uvw>}$

$L^*(hkl) = \sqrt{<hkl|G^*|hkl>}$

G et G* étant les tenseurs métriques dans l'espace direct et réciproque respectivement.

Classification des macles

Les macles sont classées selon plusieurs critères.

Classification cristallographique

L'opération qui transforme l'orientation d'un individu d'une macle en celle d'un autre individu est dite opération de macle. Celle-ci est effectuée autour d'un élément géométrique du réseau de la macle, qui est dit élément de macle : les individus de la macle sont alors symétriques par rapport à l'élément de macle. Les macles sont ainsi classées en trois catégories :

macle par réflexion, lorsque l'élément de macle est un plan réticulaire (plan de macle) ;
macle par rotation, lorsque l'élément de macle est une rangée (axe de macle) ;
macle par inversion, lorsque l'élément de macle est un point.

La surface d'accolement des individus peut être un plan ou une surface quelconque.

Classification d'après les propriétés des macles

Sur la base des valeurs de l'indice de macle et de l'obliquité, les macles sont classées en quatre catégories principales.

Classification des macles selon les valeurs de l'indice et de l'obliquité
	$n = 1$	$n > 1$
ω = 0	macle par mériédrie	macle par mériédrie réticulaire
ω > 0	macle par pseudo-mériédrie	macle par pseudo-mériédrie réticulaire

Classification d'après l'origine

Selon leur origine, les macles sont classées en trois catégories :

macles de croissance, qui se forment pendant la croissance cristalline, soit dans les premières étapes, soit par accolement tardif de cristaux ayant déjà atteinte une taille considérable ;
macles de transformation, qui se forment suite à une transition de phase dans laquelle la symétrie du cristal baisse et dans sa structure des domaines à différente orientation vont se former ;
macles mécaniques, qui se forment suite à une action mécanique, notamment une pression orientée le long d'une direction.

Classification morphologique

Les individus d'une macle peuvent être séparés par une surface plane ou irrégulière ou avoir un volume en commun. Les deux cas correspondent aux macles par contact et aux macles par pénétration, respectivement.

Selon la morphologie de l'édifice cristallin, les macles sont classées en :

macles simples, lorsque à chaque orientation correspond un seul individu ;
macles répétées, lorsque à chaque orientation correspondent plusieurs individus ; les macles répétées sont à leur tour classées en :
- macles polysynthétiques, lorsque les individus sont côte à côte et donnent à la macle un aspect strié (par exemple la macle de l'albite dans les plagioclases) ;
- macles cycliques, lorsque les individus sont forment un édifice à peu près circulaire (par exemple la macle du chrysobéryl).

Exemples de macles

Parmi les macles les plus connues, on peut citer :

les macles de Carlsbad (Karlsbad), Baveno et Manebach dans les feldspaths ;
les macles de l'albite et du péricline dans les feldspaths ;
les macles du Dauphiné, du Brésil et de la Gardette (dite aussi macle du Japon) dans le quartz ;
les macles à croix dans la staurotide ;
la macle à fer de lance dans le gypse ;
la macle à croix de fer dans la pyrite ;
les macles de la bournonite, très fréquentes sur {010}, pouvant se répéter et former des roues ou engrenages typiques.

Galerie

Quartz - Macle de la Gardette - Vizille Isère France (5,2x5cm)
Pyrite Macle en « Croix de fer » - Mine de Batère Pyrénées Orientales - France (7x5cm)
Bournonite Macle "en roue" - Les Malines, Saint-Laurent-le-Minier, Gard France (XX 6x5cm)
Adulaire (Orthoclase) - Macle de Manebach - Adula Mts, Tessin, Suisse (7x6.5cm)
Orthoclase Macle de Kalrsbad - Karlasbad (Karlovy Vary), Tchéquie
Calcite macle sur {001} - Moux Aude (XX5.1x3.2cm)

Cliquez sur une vignette pour l’agrandir

Notes et références

Voir aussi

Liens externes

Définition de « macle », par Alain Foucault (Professeur émérite au Muséum national d'histoire naturelle)
Document (76 pages, en français) d'Alain ABREAL sur les macles
(en) Théorie réticulaire des macles (Commission sur la Cristallographie Mathématique et Théorique de l'Union internationale de cristallographie)

Bibliographie

Georges Friedel Étude sur les groupements cristallins. Extrait du Bulletin de la Société de l'Industrie minérale, Quatrième série, Tomes III e IV. Saint-Étienne, Société de l’Imprimerie Théolier J. Thomas et C., 1904, 485 pp.
Georges Friedel, « Contribution à l'étude géométrique des macles », dans Bulletin de la Société française de Minéralogie, vol. 43, 1920, p. 246-295
Georges Friedel, Leçons de Cristallographie, Berger-Levrault, Nancy, Paris, Strasbourg, 1926, XIX+602 pp
Georges Friedel, « Sur un nouveau type de macles », dans Bulletin de la Société française de Minéralogie, vol. 56, 1933, p. 262-274
(en) J.D.H. Donnay, « Width of albite-twinning lamellae », dans American Mineralogist, vol. 25, n^o 9, 1940, p. 578-586 [texte intégral]

Sur les autres projets Wikimedia :

« Macle (cristallographie) », sur Wikimedia Commons (ressources multimédia)

Catégorie :

Cristallographie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Macle (cristallographie) de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

macle — ou macre 1. (ma kl ou ma kr ) s. f. Noms vulgaires de la macre flottante (onagrariées), dite aussi corniole, trapa natans, L. Nom du fruit, qui est de la grosseur et presque de la forme d une châtaigne. Mangez cette macle. macle 2. (ma kl ) s … Dictionnaire de la Langue Française d'Émile Littré
Macle — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Macle », sur le Wiktionnaire (dictionnaire universel) En cristallographie, une macle est une… … Wikipédia en Français
CRISTAUX - Cristallographie — Le nom de cristal fut d’abord réservé aux substances minérales naturelles limitées par des formes polyédriques plus ou moins parfaites. L’existence de formes polyédriques était alors considérée comme le critère essentiel de la définition du… … Encyclopédie Universelle
Joint de macle — Un joint de macle (en anglais crystal twin, littéralement « cristal jumeau ») est un joint de grain qui est également un plan de symétrie miroir pour les réseaux des cristallites. Il résulte en général d une déformation plastique… … Wikipédia en Français
Pore (cristallographie) — Pour les articles homonymes, voir Pore. En cristallographie, un pore est une cavité dans un cristal. C est un défaut volumique (à trois dimensions). Cette cavité peut être vide, ou bien contenir du gaz sous faible pression. La porosité résulte d… … Wikipédia en Français
Acid plagioclase — Albite Albite Catégorie IX : silicates Albite Zillertal, Autriche (15x14cm) … Wikipédia en Français
Analbite — Albite Albite Catégorie IX : silicates Albite Zillertal, Autriche (15x14cm) … Wikipédia en Français
Andesine — Albite Albite Catégorie IX : silicates Albite Zillertal, Autriche (15x14cm) … Wikipédia en Français
Cleavelandite — Albite Albite Catégorie IX : silicates Albite Zillertal, Autriche (15x14cm) … Wikipédia en Français
Cryptoclase — Albite Albite Catégorie IX : silicates Albite Zillertal, Autriche (15x14cm) … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Macle (cristallographie)

Sommaire